Выборочные характеристики
Дисперсия выборки из генеральной совокупности:
ДИСП(x1; x2; …; x30).
Формула вычисления выборочной дисперсии:
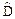 =
= 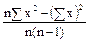 .
.
Дисперсия генеральной совокупности:
ДИСПРА(x1; x2; …; x30).
В отличие от функции ДИСП при вычислении значения функции ДИСПРА предполагается, что в параметрах функции представлена вся генеральная совокупность, а не выборка из нее.
Формула вычисления дисперсии генеральной совокупности:
D = 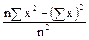 .
.
Медиана – это число, которое является серединой упорядоченной последовательности чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел – меньшие, чем медиана:
МЕДИАНА(x1; x2; …; x30).
Если количество значений четное, то функция вычисляет среднее двух значений, находящихся в середине последовательности.
Мода – это наиболее часто встречающееся или повторяющееся значение в последовательности чисел:
МОДА(x1; x2; …; x30).
Если несколько значений встречаются одинаковое количество раз, то возвращается минимальное значение.
Наименьшее k-е значение из значений диапазона ячеек:
НАИМЕНЬШИЙ(диапазон; k).
Эта функция используется для определения значения, занимающего определенное относительное положение среди значений диапазона ячеек.
Минимальное значение последовательности имеет k = 1.
Если диапазон пуст или k ≤ 0 или k превышает число ячеек диапазона, то функция возвращает значение ошибки #ЧИСЛО!.
Наибольшее k-е из значений диапазона ячеек:
НАИБОЛЬШИЙ(диапазон; k).
Среднее арифметическое:
СРЗНАЧ(x1; x2; …; x30),
где x1; x2; …; x30 – числа, имена или ссылки, содержащие числа.
Ячейки, не содержащие числа, игнорируются.
Формула вычисления среднего арифметического:
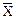 =
= 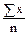
Среднее гармоническое:
СРГАРМ(x1; x2; …; x30).
Если один из аргументов функции отрицательный, то функция СРГАРМ возвращает значение ошибки #ЧИСЛО!.
Формула вычисления среднего гармонического:
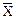 гарм. =
гарм. = 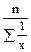 .
.
Среднее геометрическое:
СРГЕОМ(x1; x2; …; x30).
Формула вычисления среднего геометрического:
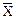 геом. =
геом. = 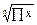 .
.
Среднее доли множества данных, отбрасывая числа с экстремальными значениями:
УРЕЗСРЕДНЕЕ(диапазон; доля),
где диапазон – интервал усредняемых значений; доля – процент значений, исключаемых из вычислений.
Например, если доля = 0,2, то отбрасываются 10% чисел с наибольшими значениями и 10% чисел с наименьшими значениями.
Значение параметра доля лежит в диапазоне [0; 1], иначе функция возвращает значение ошибки #ЧИСЛО!.
УРЕЗСРЕДНЕЕ округляет в меньшую сторону количество отбрасываемых значений до ближайшего четного целого.
Комбинаторика
Количество размещений из n элементов по m – любых упорядоченных множеств из m элементов множества, состоящего из n различных элементов:
ПЕРЕСТ(n; m).
Оба аргумента усекаются до целых.
Если n или m не является числами, то функция возвращает значение ошибки #ЗНАЧ!.
Если n ≤ 0 или m < 0 или n < m, то функция ПЕРЕСТ возвращает значение ошибки #ЧИСЛО!.
Формула расчета размещений:
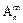 =
= 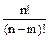 .
.
Количество сочетаний из n элементов по m – размещений, в которых не учитывается порядок элементов:
ЧИСЛКОМБ(n; m).
Формула расчета сочетаний:
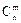 =
= 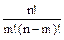 .
.
Дата добавления: 2019-04-03; просмотров: 451;
