Графический метод решения игры 2Х2
1. Найдем оптимальную стратегию для первого игрока (А):
а) Построим систему координат
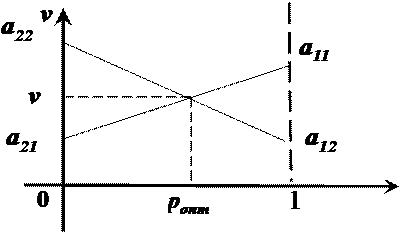 р
р
б) По оси абсцисс откладывается вероятность рÎ[0,1], равная 1.
в) По оси ординат – выигрыши игрока А при стратегии А2, а на прямойр= 1 – выигрыши при стратегии А1
г)Находим точку пересечения прямых, которая и дает оптимальное
решение матричной игры для игрока А (ропт, v).
2. Найдем оптимальную стратегию для второго игрока (В):
а) По оси абсцисс откладывается вероятность q1Î[0,1], равный 1.
б) По оси ординат – выигрыши игрока B при стратегии B2, а на прямой q = 1 – выигрыши при стратегии B1
в) Находим точку пересечения прямых, которая и дает
 оптимальное решение матричной игры для игрока B (qопт, v)
оптимальное решение матричной игры для игрока B (qопт, v)
Пример 6. Матричная игра 2х2 задана следующей матрицей
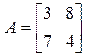
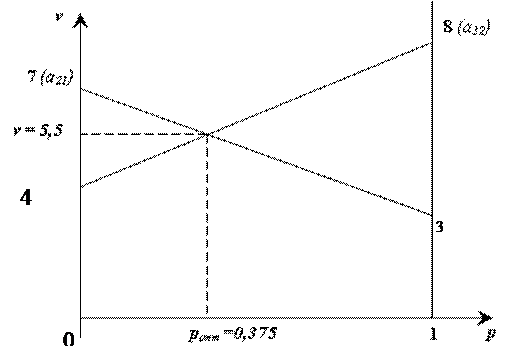
Найтирешение игры графическим методом.
Сначала необходимо определить, решается ли данная игра в чистых стратегиях, то есть существует ли седловая точка или нет.
α = 4, β = 7, при этом цена игры v Î [4, 7]
α<β - игра не имеет седловой точки, и поэтому имеет решение в смешанных стратегиях.
Для игр с платежными матрицами большой размерности отыскание оптимального решения можно упростить, если уменьшить их размерность путем исключения дублирующих и заведомо невыгодных (доминируемых) стратегий.
Упрощение матрицы происходит согласно следующим правилам:
1.Если в платежной матрице игры все элементы строки (столбца) равны соответствующим элементам другой строки (столбца), то соответствующее этим строкам(столбцам) стратегии называются дублирующими и одна из них исключается из матрицы.

2.Если в платежной матрице игры все элементы некоторой строки, определяющей стратегию Аi игрока А, не больше (меньше или некоторые равны) соответствующих элементов другой строки, то стратегия Аi называется доминируемой (заведомо невыгодной) и исключается из матрицы.
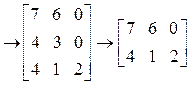
3.Если в платежной матрице игры все элементы некоторого столбца, определяющего стратегию Вi игрока В не меньше (больше или некоторые равны) соответствующих элементов другого столбца, то стратегия Вi называется доминируемой (заведомо невыгодной) и исключается из матрицы.
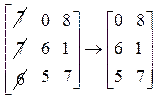
Решение матричной игры не изменится, если из платежной матрицы исключить строки и столбцы, соответствующие дублирующим и доминируемым стратегиям.
Пример 7. Упростим матричную игру.
Стратегии игрока А. Необходимо сравнить последующую строку с предыдущей поэлементно.
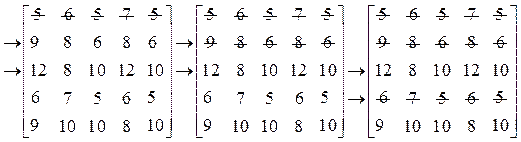
Все соответствующие элементы первой строки меньше соответствующих элементов второй строки, значит, первую строку исключаем из матрицы. Соответствующие элементы второй строки меньше или равны соответствующих элементов третьей строки, поэтому исключаем вторую стратегию игрока А как заведомо невыгодную. Все элементы четвертой строки меньше элементов третьей строки, поэтому четвертая строка исключается из матрицы. Сравнивая третью и пятую строку, видим, что соответствующие элементы этих строк не больше друг друга. Следовательно, из них нет заведомо невыгодных стратегий.
Стратегии игрока В.Платежная матрица имеет следующий вид.
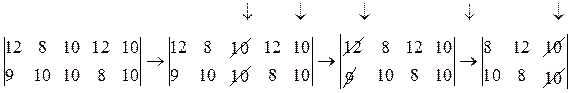
Сравнивается каждый последующий столбец с предыдущим поэлементно. Существуют дублирующие стратегий игрока В – это третья и пятая стратегии. Любую из них исключаем из игры. При сравнении первого и второго столбца - заведомо невыгодных стратегий нет. При сравнении первого и четвертого столбца видно, что соответствующие элементы первого столбца больше и равны соответствующих элементов четвертого столбца, следовательно, первая стратегия заведомо невыгодна. После сокращений осталась матрица игры 2x2.
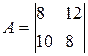
Верхняя и нижняя цена игры равныα = 8, β = 10, цена игры v Î [8, 10].
Дата добавления: 2019-04-03; просмотров: 2565;
