Игры с матрицей 2 Х 2
Аналитический метод. Пусть дана игра с платёжной матрицей
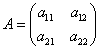
Если эта матричная игра имеет седловую точку, то она имеет решение в чистых стратегиях.
Если же игра не имеет седловой точки, то она имеет решение в оптимальных смешанных стратегиях. Для этого простейшего случая матричной игры при её решениях путём сведения к задаче линейного программирования были найдены формулы стратегий игроков и цены игры, благодаря которым такая игра решается менее трудоёмким способом.
Формула для нахождения оптимальной смешанной стратегии первого игрока:
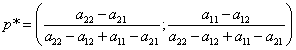 .
.
Формула для нахождения оптимальной смешанной стратегии второго игрока:
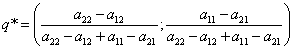 .
.
Формула для нахождения цены игры:
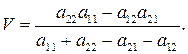
Пример 5. Дана матричная игра с платёжной матрицей
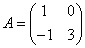 .
.
Найти оптимальные смешанные стратегии игроков и цену игры аналитическим методом.
Решение. Оптимальные смешанные стратегии первого игрока получаем по соответствующей из приведённых формул:
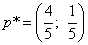 .
.
Оптимальные смешанные стратегии второго игрока получаем также по соответствующей формуле:
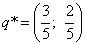 .
.
Цена игры: 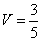 .
.
Дата добавления: 2019-04-03; просмотров: 957;
