Структурные средние величины.
Для характеристики структуры вариационных рядов применяются показатели особого рода, которые можно назвать структурными средними.
Мода– значение признака, наиболее часто встречающееся в исследуемой совокупности.
Медиана– значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Для дискретных вариационных рядов модойбудет значение варианта с наибольшей частотой. Вычисление медианыв дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.
Рассмотрим определение моды и медианы по несгруппированным данным.
Пример 6: Предположим, рабочие бригады, состоящей из 9 человек имеют следующие тарифные разряды: 4 3 4 5 3 3 6 2 6.
Так как в данной бригаде больше всего рабочих 3-го разряда этот тарифный разряд и будет модальным.
Для определения медианы необходимо провести ранжирование:
2 3 3 3 4 4 5 6 6.
Центральным в этом ряду является рабочий 4-го разряда, следовательно, данный разряд и будет медианным.
Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальному закону распределения совокупности. Проиллюстрируем ее познавательное значение следующим примером.
Пример 7: Допустим, нам необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 100 до 200 долл. в месяц, а месячные доходы последнего составляют 50 000 долл.
| № п/п | … | … | ||||||||
| Доход, долл. | … | … |
Если мы воспользуемся средней арифметической, то получим средний доход, равный примерно 600 - 700 долл., который не только в несколько раз меньше дохода 100-го человека, но и имеет мало общего с доходами остальной части группы. Медиана же, равная в данном случае 163 долл., позволит дать объективную характеристику уровня доходов 99% данной группы людей.
Пример 8. Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения).
Предположим, распределение рабочих уже не отдельной бригады, а всего предприятия в целом по тарифному разряду имеет следующий вид:
| Тарифный разряд | Численность рабочих, человек | Накопленная частота |
| 12 | ||
| 60 | ||
| 116 | ||
| 176 | ||
| 190 | ||
| Всего: |
Определение моды по дискретному вариационному ряду не составляет большого труда - наибольшую частоту (60 человек) имеет 5-й тарифный разряд, следовательно, он и является модальным.
Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда (NMe):
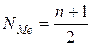 , где
, где 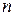 – объем совокупности.
– объем совокупности.
В нашем случае: 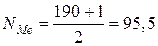 .
.
Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 95-м и 96-м рабочими. Необходимо определить, к какой группе относятся рабочие с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Медианным является 4-й тарифный разряд.
В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул:
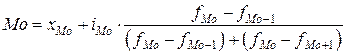 ,
,
где 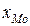 – нижняя граница значения интервала, содержащего моду;
– нижняя граница значения интервала, содержащего моду;
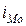 – величина модального интервала;
– величина модального интервала; 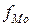 - частота модального интервала;
- частота модального интервала; 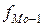 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному; 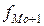 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Медиана интервального ряда распределения определяется по формуле:
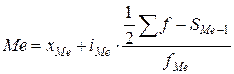 ,
,
где 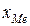 – нижняя граница значения интервала, содержащего медиану;
– нижняя граница значения интервала, содержащего медиану;
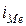 – величина медианного интервала;
– величина медианного интервала;
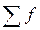 – сумма частот;
– сумма частот;
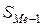 – сумма накопленных частот, предшествующих медианному интервалу;
– сумма накопленных частот, предшествующих медианному интервалу;
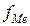 – частота медианного интервала.
– частота медианного интервала.
Пример 9.Рассчитаем моду и медиану по данным таблицы:
Распределение семей города по размеру среднедушевого дохода в январе 1998г.
| Группы семей по размеру дохода, руб. | Число семей | Накопленные частоты | Накопленные частоты, % к итогу |
| До 500 | |||
| 500-600 | 1 300 | ||
| 600-700 | 1 700 | 3 000 | |
| 700-800 | 2 500 | 5 500 | |
| 800-900 | 2 200 | 7 700 | |
| 900-1000 | 1 500 | 9 200 | |
| Свыше 1000 | 10 000 | ||
| Итого: | 10 000 | – |
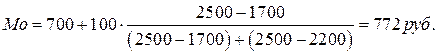
Следовательно, наибольшее число семей имеют среднедушевой доход 772 руб.
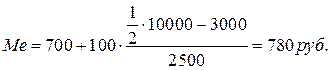
Таким образом, половина семей города имеет среднедушевой доход менее 780 руб., остальные семьи – более 780 руб.
Дата добавления: 2019-04-03; просмотров: 768;
