Тема 4. Сводка и группировка
1.Понятие сводки и группировки
2.Виды группировок
3. Группировочные признаки
4. Статистические ряды распределения
5 Статистические таблицы
6.Статистические графики
1. Специфика предмета статистики – это специфика статистического метода, он включает:
- сбор данных – статистическое наблюдение;
- обобщение данных наблюдения (включает сводку и группировку);
- представление данных в подходящей форме и компактно;
- анализ и интерпретацию.
В результате первой стадии статистического исследования - статистического наблюдения - получают сведения о каждой единице совокупности. Задача второй стадии статистического исследования состоит в том, чтобы упорядочить и обобщить первичный материал, свести его в группы и на этой основе дать обобщенную характеристику совокупности. Этот этап в статистике называется сводкой.
Статистическая сводка- систематизация единичных фактов, позволяющая перейти к обобщающим показателям, относящимся ко всей изучаемой совокупности и ее частям, и осуществлять анализ и прогнозирование изучаемых явлений и процессов.
Различают:
- простую сводку (подсчет только общих итогов);
- статистическую группировку.
Статистическая группировкасводится к расчленению совокупности на группы по существенному для единиц совокупности признаку. Группировка позволяет получить такие результаты, по которым можно выявить состав совокупности, характерные черты и свойства типичных явлений, обнаружить закономерности и взаимосвязи. Группировка является основным методом обработки собранной информации.
Чтобы сгруппировать данные, необходимо ознакомиться со всеми результатами наблюдения и сделать первичные выводы о характеристиках изучаемого объекта. Именно поэтому группировку иногда называют первичным анализом данных.
Способ разработки статистической сводки может быть:
- централизованным;
- децентрализованным.
При централизованной сводкевсе данные сосредоточиваются в одном месте и сводятся по разработанной методике.
При децентрализованной сводкеобобщение материала осуществляется снизу доверху по иерархической лестнице управления, подвергаясь на каждом из них соответствующей обработке.
Положив начало научной систематизации и обработке исходной информации, сводка и группировка статистических данных служат тем самым базой для осуществления всестороннего анализа и прогнозирования коммерческой деятельности на рынке товаров и услуг.
2. Выделяют несколько видов группировок, применение которых обусловлено характером единиц совокупности:
• типологическая группировка - подразделяет единицы в зависимости от их типа. Применяется, как правило, для группировок по атрибутивным (качественным) признакам. Отрицательной стороной является подверженность субъективным взглядам исследователя при отнесении единиц к различным типам явления;
• структурная группировка - характеризует структуру изучаемой совокупности, т.е. отвечает на вопросы:
- какие части можно выделить в объекте наблюдения,
- каково соотношение между ними (или какой удельный вес в целом имеет каждая часть).
Как правило, осуществляется по одному признаку;
• аналитическая группировка - характеризует степень влияния одного фактора объекта на другой. Причем влияющий фактор называют признак-фактор, а параметр, подверженный влиянию, - признак-результат.
Иногда учитывается несколько признаков-факторов, тогда такая группировка называется многомерной (многофакториой).
Образование групп по двум и более признакам, взятым в определенном сочетании, называется комбинированной группировкой.При этом группировочные признаки принято располагать, начиная с атрибутивного (качественного), в определенной последовательности, исходя и 1 логики взаимосвязи показателей. Применение комбинированных группировок обусловлено многообразием экополитических явлений, а также необходимостью их всестороннего изучения. Примером комбинированной группировки может служить разделение образованных групп по формам хозяйствования на подгруппы по уровню рентабельности или по другим признакам (производительность труда, фондоотдача и т.д.).
Особенностьюаналитических группировок является тот факт, что группировка считается выполненной после применения элементов корреляционно-регрессионного анализа, т.е. после количественного определения меры зависимости между факторами.
Наиболее сложный вопрос теории группировок - выбор группировочного признака.
3.Социально-экономические явления отличаются большим многообразием форм своего развития, и поэтому при группировке встает вопрос о выборе того признака, который адекватен цели исследования и характеру исходной информации. Определяющими являются признаки, наиболее полно и точно характеризующие изучаемый объект, позволяющие выбрать его типичные черты и свойства.
Группированные признаки (или основание группировки) - это признаки, по которым производится распределение единиц наблюдаемой совокупности на группы. Так, при группировке населения по месту проживания выделяются две группы: городское и сельское население. Число возможных групп статистических данных может быть ограничено соответствующими признаками (атрибутами) такими как иол, возраст, образование, классовая принадлежность и т.п. Однако группировки могут формироваться по множеству других признаков и не только в статике на определенную дату, но и в динамике, т.е. на протяжении каких-то лет, взятых в определенном интервале.
Поскольку единицы совокупностей подвергаемых группировке, обладаю! многими признаками, то группы могут быть образованы по одному или нескольким признакам, взятым в определенной комбинации. Группировки по одному признаку называются простыми, группировки по двум и более признакам, взятым в сочетании с другим, называется комбинационными. Примером комбинационных группировок может быть таблица численности городского и сельского населения в нашей стране по данным переписи 1970 г. Указанные в таблице группировки населения по признаку «городское и сельское население» не только представлены в динамике, т.е. в процессе исторического развития страны с 1913 по 1970 г., но и раскрывают этот процесс в абсолютных и относительных числах.
По форме выражения группировочные признаки могут быть:
- атрибутивными (качественными);
- количественными(численными).
При этом количественные признаки, в свою очередь, могут быть:
- дискретными (прерывными), значения которых выражаются только целыми числами (число комнат в квартире, число человек в семье и т. д.),
- интервальными (непрерывными), принимающими как целые, так и дробные значения (рост человека, вес, зарплата, метраж квартиры, объем проданных населению товаров в стоимостном выражении, сумма издержек обращения).
Вопрос о числе групп и границах интервала для каждого вида группировок должен решаться по-разному, исходя из целей исследования, значения изучаемого признака, объема коммерческой деятельности и т.д.
Количество групп во многом зависит от того, какой признак служит основанием группировки. Так, нередко атрибутивные группировочные признаки предопределяют число групп. По аналогии также расчленяется совокупность по дискретному признаку, изменяющемуся в незначительном диапазоне.
Различают:
- открытые интервалы,
- закрытые интервалы.
Открытые интервалы имеют какую-нибудь одну обозначенную границу в первой и последней интервальной группе, а замкнутые - и верхнюю и нижнюю границы интервала.
Интервалы групп устанавливаются только при значительной колеблемости дискретного признака и при непрерывно изменяющемся количественном признаке (величина зарплаты).
Величина интервала - это разность между максимальными и минимальными значениями признака в каждой группе. Эту величину можно определить и как разность между верхними или нижними границами значений признака в смежных группах
Интервалы бывают:
- равные (построение замкнутых интервалов);
- неравные (построение открытых интервалов).
Величину интервала можно определить по формуле:
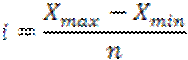
где i - величина интервала,
Xmax и Xmin - максимальное и минимальное значение признака в совокупности,
п - число групп.
Пример.
Сформировать 3 группы рабочих по средней зарплате. Известно, что самая высокая з/пл 9200 руб., самая низкая 5600 руб.
1) Определяем величину интервала по формуле:
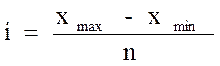
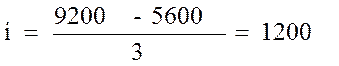
2) Сформируем группы рабочих по средней з/пл
1 гр. 5600 – 6800
2 гр. 6800 – 8000
3 гр. 8000 - 9200
4.Первым и наиболее простым способом обобщения статистических данных являются ряды распределения.
Статистическим рядом распределения называют численное распределение единиц совокупности по изучаемому признаку. В зависимости от признака ряды делятся на вариационные (количественные) и атрибутивные (качественные).
Вариационные ряды могут быть дискретными или интервальными.
Дискретный ряд распределения - это ряд, в котором численное распределение признака выражено одним конечным числом (например, распределение рабочих по разрядам).
Интервальный ряд распределения- это ряд, в котором значения признака заданы в виде интервала. Интервалы в рядах распределения могут быть неравными - прогрессивно возрастающими или прогрессивно убывающими. Это характерно для совокупностей с большой колеблемостью значений признака.
Элементы рядов распределения:
1. Варианта - это отдельное значение варьирующего признака, которое он принимает в ряду распределения.
2. Частота - это число, которое показывает, сколько раз встретилась варианта в данной совокупности.
При построении интервальных рядов распределения необходимо определить:
- какое число групп следует образовать;
- какие взять интервалы (равные, неравные, закрытые, открытые). Эти вопросы решаются на основе экономического анализа сущности изучаемых явлений, поставленной цели и характера изменений признака.
Интервалы не должны быть:
- слишком широкими, так как в противном случае качественно различные объекты могут попасть в одну и ту же группу (нельзя, например, строить такие возрастные интервалы: 0—15 лет; 16—30 лет),
- не должны быть слишком узкими, поскольку и в этом случае число единиц в той или иной группе окажется незначительным и характеристики групп не будут типичными.
Интервальные ряды изображают - на графике с помощью гистограмм.
Дискретные ряды изображают - с помощью полигона распределения.
Обобщение данных и виде ряда распределения позволяет видеть вариацию и состав совокупности по изучаемому признаку, сравнивать между собой группы, изучать их в динамике.
Пример.
Сделать группировку рабочих по стажу и построить:
1) Вариационный дискретный ряд.
2) Вариационный интервальный ряд, образовав 2 группы с равными интервалами.
3) Указать варианту и частоту.
Данные о стаже рабочих: 3 2 5 6 6 1
1 3 1 5 6 6
2 4 5 4 6 5
1) Ряд распределения рабочих по стажу
| Стаж работы | Итого | ||||||
| Количество рабочих |
Вид РР: вариационный дискретный ряд.
Варианта: стаж работы
Частота: число рабочих
2) Ряд распределения рабочих по стажу
| Стаж работы | 1-4 | 4-7 | Итого |
| Количество рабочих |
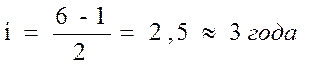
Вид РР: вариационный интервальный ряд.
Варианта: стаж работы
Частота: число рабочих
5. Результаты группировок находят свое выражение в виде сводных таблиц.
Таблица - это компактное изображение собранного материала в виде системы строк и столбцов, на пересечении которых приводятся данные, характеризующие изучаемое явление.
Статистическая таблица состоит из следующих элементов:
общий заголовок - отражает суть всей таблицы, содержит указание на характеризуемый признак объекта исследования, время, место наблюдения (иногда единицы измерения признака);
подлежащее - характеризуемый в таблице объект исследования (находится в левой части таблицы по строкам);
сказуемое - показатели, характеризующие подлежащее (располагается в верхней части по графам);
итоговая строка - может находиться в начале (тогда сопровождается нижеследующей строкой «в том числе») или в конце подлежащего. В тех графах итоговой строки, и которых по смыслу не могут быть подсчитаны результаты, ставится «X»;
цифровые данные - количественная характеристика исследуемого объекта (в случае отсутствия данных ставится «..» или пишется «нет сведений», а в случае отсутствия типа явления ставится «-»);
сетка - пересечение горизонтальных и вертикальных линий.
Все таблицы можно разделить на три группы:
1. Таблицы простые, или перечневые, в которых содержатся сводные показатели или перечень отдельных объектов без расчленения совокупности на группы.
2. Групповые таблицы, в которых статистическая совокупность расчленена на отдельные группы и каждая из этих групп охарактеризована рядом показателей.
3.Комбинационные таблицы, в которых статистическая совокупность разбита на группы по нескольким признакам (таким образом, в таблице получается комбинация групп).
По построению сказуемого различают:
- простые;
-комбинированные таблицы.
При простой разработке каждая графа сказуемого отдельно друг от друга характеризует подлежащее. При комбинированной таблице показатели сказуемого разрабатываются в сочетании друг с другом.
6. Графическое представление статистической информации применяется для более наглядного отображения исследуемых процессов.
Статистические графики - это условные изображения статистических данных в виде точек, линий или фигур,
Схематически все множество графических представлений статических данных разделяют на два класса:
- диаграммы;
- линейные изображения.
Выбор вида применяемого графика зависит от отображаемых данных. Например, для изображения структурного распределения совокупности, как правило, применяется круговая диаграмма.
Статистический график состоит из следующих элементов:
графический образ - геометрические значки, с помощью которых выражаются статистические показатели;
поле графика - ограниченная плоскость, на которой располагается график;
масштабные ориентиры - система мер и шкал, принятых для отображения данных.
К классу линейных графиков относятся:
- полигон,
-кумулятивная кривая,
-кривая концентрации,
- огива.
Полигоном частотназывают ломаную, отрезки которой соединяют точки (х1, т2), ... ,(хk, , тk ). Иногда крайние точки соединяют с точками, имеющими нулевую ординату.
Кумулятивная кривая (кривая сумм) - ломаная, составленная по последовательно суммированным, т.е. накопленным частотам или относительным частотам. При построении кумулятивной кривой дискретного признака на ось абсцисс наносятся значения признака, а ординатами служат нарастающие итоги частот. Соединением вершин ординат прямыми линиями получают кумуляту.
При построении кумуляты интервального признака на ось абсцисс откладываются границы интервалов и верхним значениям присваивают накопленные частоты. Кумулятивную кривую называют полигоном накопленных частот.
Если на ось ординат нанести значение признака, а накопленные частоты — на ось абсцисс, то получим кривую, называемую огивой.
Диаграмма- это графическое изображение, наглядно показывающее соотношение между сравниваемыми величинами. Диаграммы бывают различных видов:
- полосовые (ленточные),
- столбиковые,
- квадратные,
- круговые,
- секторные,
- фигурные,
- радиальные,
- знак Варвара.
Основным видом столбиковых диаграмм являются гистограммы.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат частотные интервалы длины, а высоты равны отношению Мi/h (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними на расстоянии Мi/h проводят отрезки, параллельные основанию.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых случат частичные интервалы длиной h, а высоты раины Wi/h. Гистограмма относительных частот - аналог плотности распределения непрерывной случайной величины. Иногда высоты прямоугольников и гистограмме не делят на h, но указывают над столбиками значение высоты и над осью ординат пишут, что ее значение надо делить на h. Такую гистограмму называют масштабированной.
При построении квадратных и круговых диаграмм площади квадратов или кругов выражают изображаемые величины.
Круговые секторные диаграммы применяют для графического изображения составных частей целого. Чтобы легче различать сектора, используют различную раскраску или штриховку.
Радиальные диаграммы строятся в полярной системе координат и используются для изображения признаков, периодически изменяющихся во времени (в большинстве своем сезонных колебаний). Вычисляется среднее арифметическое,затем строится окружность радиуса, равного среднему арифметическому. Данная окружность делится на нужное число секторов (обычно 12) и на каждом радиальном направлении откладываются точки в соответствии со значениями Xi.
Фигурные диаграммы строятся двумя основными способами: данные изображаются либо фигурами различных размеров, либо разной численностью фигур одинакового размера.
Диаграмма «знак Варзара» названа в честь русского статистика. С помощью данной диаграммы можно изображать многомерные признаки на плоскости посредством прямоугольников с разным соотношением между основанием и высотой. Одна из компонент признака изображается основанием прямоугольника, вторая - его высотой, третья равна произведению двух других размером получившейся площади.
Дата добавления: 2019-04-03; просмотров: 972;
