Крутильные колебания

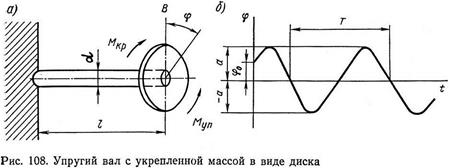
При очередной вспышке топлива в рабочем цилиндре происходит закручивание коленвала и гребного вала, а далее раскручивание под действием упругих сил. Такие колебания наз. крутильными.

М_ин + М_упр=0

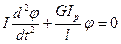
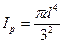
I – момент инерции массы

G – момент упругости при сдвиге материала вала

I_p – полярный момент инерции сечения вала

Частота свободных крутильных колебаний системы зависит от жесткости вала и момента инерции массы. Амплитуды колебаний различны, а период и частота остаются такими же.

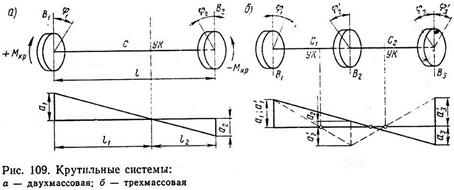
Рассомтрим двух- и трехмассовые системы

Неподвижное сечение вала наз. узлом колебаний

Двухузловая форма колебаний возникает, если в рассматри­ваемой системе к ее крайним массам приложить одинаковые моменты одного знака, закручивающие вал на углы φ₁ и φ₃', а к средней массе — момент противоположного цикла (φ₂').

Практический интерес при расчетах крутильных схем вало-провода судовых дизелей представляют только низшие формы колебаний: одно-, двух- и реже трехузловая. Четырех- и- пятиузловые формы колебаний представляется необходимым исследо­вать только в исключительных случаях, когда система имеет большое число масс (более 15—20).

Расчет крутильной системы, имеющий конечной целью опре­деление запретных зон частот вращения вала двигателей, допус­кает замену действительной системы эквивалентной дискретной.

Расчет крутильной системы с целью определения запретных зон частот вращения вала допускает замену действительной системы эквивалентной дискретной.

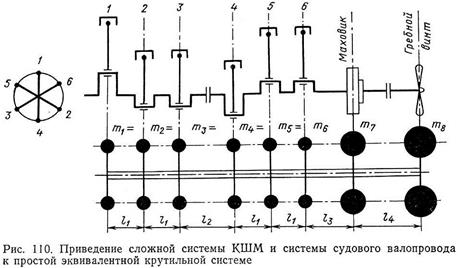
Приведение (замена) действительной крутильной системы к эквивалентной дискретной производят для упрощения и удобст­ва расчета свободных крутильных колебаний. При этом действи­тельные массы заменяют эквивалентными им по динамическим свойствам, а в целом сложная система кривошипно-шатунного механизма, системы судового валопровода (включая и гребной винт) приводят к простой эквивалентной системе (рис. 110). Эта система состоит из цилиндрического вала постоянного диаметра и эквивалентных сосредоточенных масс, расположенных на оди­наковом расстоянии от оси вала.

Вынужденные крутильные колебания возбуждаются периодически от движ. сил.

P_D=P_г+P_u+P_т P_т=m_sg

Переменная величина крутящего момента от движущей силы изменяющаяся по период кривой, может быть представлена рядом Фурье.

Переменная величина крутящего момента от движущей силы, изменяющаяся по периодической кривой, может быть представ­лена рядом Фурье, т. е. суммой постоянного члена среднего кру­тящего момента и некоторого числа гармонических составля­ющих, которые являются основными возбудителями крутильных колебаний:

М_к=М_ср+М₁sin(ω_вt+ψ₁)+М₂sin(2ω_вt+ ψ₂) +…+ М_isin(iω_вt+ ψ_i)+…,

где М_ср — средний крутящий момент (колебаний не возбуждает);

M_i , ω_в , ψ_i —амплитуда, частота и начальная фаза гармоники кру­тящего момента.

Такое разложение момента М_к называют гармоническим ана­лизом крутящего момента двигателя.

Порядком гармоники называют число полных периодов, со­вершаемых данной гармоникой за один оборот коленчатого вала.

Гармоники, порядок которых равен или кратен числу вспы­шек за один оборот вала, называют главными.

Гармоники, имеющие самый низкий порядок, называют основ­ными. Гармонический анализ тангенциальных диаграмм дизелей, соответствующих различным pi (средним индикаторным давлени­ям), даст возможность определять амплитуды гармонических со­ставляющих.

Амплитуда вынужденных колебаний сохраняет свою величину постоянной при наличии трения в системе только потому, что по­глощаемая энергия непрерывно восстанавливается за счет рабо­ты возмущающих сил.

Амплитуды вынужденных колебаний при больших значениях возмущающих моментов могут быть весьма значительными. Уве­личение амплитуды колебаний сопровождается пропорциональ­ным ростом напряжений от крутильных колебаний в некоторых элементах и сечениях системы валопровода, что ведет, к устало­сти металла и возможному его разрушению.