Список используемых обозначений и сокращений

КШМ – кривошипно-шатунный механизм;

КВ – коленчатый вал;

МОД – малооборотный двигатель;

СОД – среднеоборотный двигатель;

ВОД – высокооборотный двигатель;

ЦПГ – цилиндропоршневая группа;

ВМТ – верхняя мертвая точка;

НМТ – нижняя мертвая точка;

ЦМ – центр масс;

ПДМ – поступательно движущиеся массы;

ВМ – вращающиеся массы;

ПКВ – поворот КВ;

ДЭУ – дизельная энергетическая установка;

ПК – пропульсивный комплекс;

н. у. – нормальные условия;

ГВ – гребной винт;

ТК – турбокомпрессор

Для кинематической связи поршней с КВ используют три типа КШМ:

1. Центральный (рисунок 1). Ось цилиндра пересекается с осью КВ.

2. Деаксиальный (ось цилиндров не пересекает ось КВ, а смещена относительно неё на величину а, называемую десаксажем). Величина десаксажа

а≤0,1r

Применяется в малоразмерных ВОД. Уменьшается сила, прижимающая поршень ко втулке на такте расширения. При этом уменьшается работа трения и износ ЦПГ.

3. С прицепным шатуном (одним или несколькими). К каждой шатунной шейке крепится один шатун, называемый главным, а остальные, называемые прицепными, крепятся шарнирно к нижней головке главного шатуна.

Существуют V-образные и звездообразные двигатели такого типа.

В СДВС наиболее распространен центральный тип, для которого будем рассматривать все вопросы динамики.

Основными конструктивными параметрами КШМ являются радиус кривошипа r, длина шатуна L_ш и их отношение

,

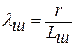называемое постоянной механизма. При анализе КШМ угол поворота кривошипа φ, отсчитываемый в направлении его вращения от положения ВМТ

,

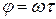рад, принимается незави­симой переменной, определяющей положение механизма.

Угловая скорость кривошипа ω при кинематических и дина­мических расчетах принимается постоянной и равна, с^-1:

,

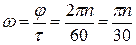где τ - время перемещения кривошипа на угол φ, с.

Угловое перемещение кривошипа φ°:

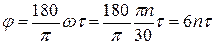
Угол отклонения шатуна от оси цилиндра β°:

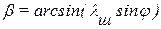
Перемещение поршня S_φ отсчитывается от положения в ВМТ и является функцией угла поворота кривошипа 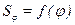. Из рисунка 1. а следует, что

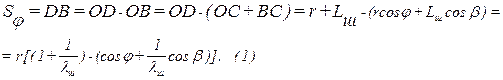
Эта формула является точной, но неудобной для практиче­ского использования, так как она содержит две связанные перемен­ные φ и β, поэтому в расчетах часто используют приближенную формулу, м:

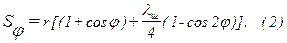
Скорость поршня при постоянной угловой скорости вращения КВ непостоянна. Среднее значение скорости поршня, м/с:

C_m=Sn/30,

где n – частота вращения КВ, об/мин.

Мгновенное значение скорости по времени, м/с:

v=dS_φ/dτ=dS_φ/dφ*ω=rω(sinφ+λ_ш/2*sin2φ).

Ускорение, м/с²:

j=dv/dτ=dv/dφ*ω=rω²(cosφ+λ_ш*cos2φ).

Силы, действующие на КШМ

На КШМ действуют силы:

- давления газов;

- инерции движущихся масс;

- тяжести;

- трения;

- полезного сопротивления на КВ.

Силы трения по сравнению с другими силами невелики. Поэтому в динамических расчетах ими пренебрегают, но учитывают их механическим КПД двигателя. Силы тяжести целесообразно учитывать в тех случаях, когда их относительная величина

p_T>0,015р_z.

Такие силы тя­жести возникают в малооборотных дизелях.

Силы и моменты, действующие на КШМ, необходимо знать для расчета деталей на прочность, оценки работоспособности подшипников, определения неравномерности вращения коленча­того вала, проверки уравновешенности двигателя и для решения других задач. Определять силы и моменты удобно в относи­тельных величинах, т. е. отнесенных к единице площади поршня F_n.

Определение приведенных масс

В динамических расчетах КШМ действительные массы движущихся частей для упроще­ния расчетов заменяются приведенными массами, сосредоточен­ными в тех точках КШМ, законы движения которых известны. При этом массы, сосредоточенные в одной и той же точке, сум­мируются. Динамическое действие приведенных масс должно быть эквивалентно действию реальных. На рисунке 2 показаны динамические модели КШМ и его отдельных частей, состоящих из жестких невесомых звеньев, с кинематическими параметрами, как и у реальных КШМ, и приведенных масс.

Приведенные массы шатуна

Шатун совершает сложное движение в вертикальной плоскости (рисунок 2, а), при этом точка В совершает поступательное движение, а точка А — вращательное. Поэтому массу шатуна М_ш делят на две приведенные массы М_шs и М_шr, сосредоточенные в этих точках. Масса М_шs сосредо­точена в центре верхней головки шатуна и совершает поступательное движение, а масса М_шr находится в центре шатунной шейки и совершает вращательное движение. При замене массы шатуна двумя приведенными массами должны быть соблюдены условия статической эквивалентности

М_ш=М_шs+M_шr, M_шsa=M_шrb,

где a и b - расстояние от центра массы шатуна до центров приведенных масс. Из этих равенств следует, что:

М_шs=М_ш*b/(a+b)=M_ш*b/L_ш; М_шr=М_ш*a/(a+b)=M_ш*a/L_ш.

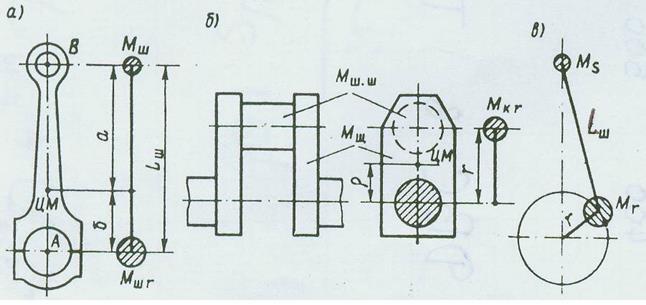
Приведенные массы кривошипа. Масса рамовых шеек пол­ностью уравновешена, так как вращается вокруг собственной оси. Неуравновешенная масса кривошипа состоит из массы двух щек 2М_щ и массы шатунной шейки М_ш.ш (рисунок 2, б). Эти неуравновешенные вращающиеся массы заменяются одной, при­веденной к радиусу кривошипа, М_кr. Масса шатунной шейки на­ходится на расстоянии r от центра вращения и не требует приве­дения. Массу щеки М_щ с центром массы, находящимся на рас­стоянии ρ от оси вращения, заменяют приведенной к радиусу кривошипа М_щr исходя из условия равенства центробежных сил действительной и приведенной масс, т.е. М_щρω²=М_щrrω².

От­сюда приведенная масса одной щеки М_щ=2М_щρ/r. Общая при­веденная масса неуравновешенных вращающихся частей криво­шипа

М_кr = М_ш.ш + 2М_щr = М_ш.ш + 2M_щρ/r

Масса поршня М_n совершает только поступательное движе­ние и считается сосредоточенной в центре поршневого пальца, а в крейцкопфных двигателях — в центре поперечины. В массу поршня включают массу всех деталей, соединенных с ним и со­вершающих поступательное движение.

Общая масса поступательно движущихся частей, кг:

М_s=М_n+М_шs=Ма + М_шb/L_ш.

Общая масса неуравновешенных вращающихся частей, кг:

М_r=М_кr+М_шr=М_ш.ш+2М_щρ/r+М_ша/L_ш.

Для удобства расчетов абсолютные значения массы заменяют относительными (кг/м²), т. е.

m_s=M_s/F_n, m_r=M_r/F_n.

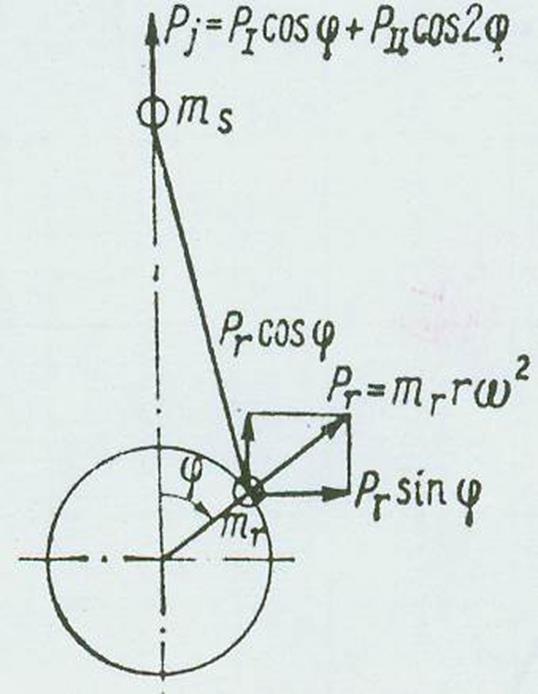
Силы инерции. При работе двигателя от поступательно дви­жущихся масс (ПДМ) и неуравновешенных вращающихся масс (ВМ) на КШМ действуют силы инерции (рисунок 3).

Сила инерции ПДМ приложена в центре поршневого пальца, действует вдоль оси цилиндра и равна, МПа:

P_j=-m_sj=-m_srω²(cosφ+λ_ш+cos2φ)=P_Icosφ+P_IIcos2φ. (5)

Сила Р_j состоит из сил инерции первого порядка P_Icosφ и второго порядка P_IIcos2φ, где

P_I=-m_srω² и P_II=-m_srω²λ_ш — амплитуды соответствующих сил инерции. Силы инерции пер­вого порядка в 3,5…5 раз больше сил инерции второго порядка. За один оборот коленчатого вала силы инерции первого порядка меняют направление один раз, а силы второго порядка — два­жды. В районе ВМТ силы инерции препятствуют движению поршня, а в районе НМТ — способствуют ему. Значения сил инерции в ВМТ получим из формулы (5) при φ = 0°, а в НМТ при ф = 180°:

P_jBMT=-m_srω(1+ λ_ш); P_jHMT=m_srω(1- λ_ш).

Сила инерции ВМ постоянна по значению, приложена в цен­тре шатунной шейки, направлена по кривошипу от центра вра­щения и равна, МПа:

Р_r = m_rrω².

Разложив силу Р_r, получим ее вертикальную Р_rсоsφ и гори­зонтальную Р_rsinφ составляющие, которые, действуя в соответ­ствующих плоскостях, изменяют свое направление один раз за оборот, т. е. они первого порядка.

Суммарные силы инерции, действующие на двигатель в вер­тикальной плоскости:

P^в_иΣ=P_j+P_rcosφ=P_Icosφ+P_IIcos2φ+ P_rcosφ;

в горизонтальной плоскости:

P^г_иΣ = Р_гsinφ.

Силы давления газов

На поршень со стороны камеры сго­рания действует сила от давления газов в цилиндре двигателя Р_r (рисунок 4). Она приложена в центре поршневого пальца и действует вдоль оси цилиндра.

Силы давления газов, действуя на поршень - P_r и на крышку цилиндра – (-P_r), взаимоуравновешиваются внутри двигателя и на его опоры не передаются. Вне двигателя силы давления газов проявляются в виде вращающего М_вр и опрокидывающего М_опр моментов. Относительное значение силы давления газов в зависимости от угла поворота кривошипа Р_r=f(φ) определяется аналитически или графически по расчетной или действи­тельной индикаторной диаграмме.

При определении по индика­торной диаграмме в координатах р — V (рисунок 5) на участке перемещения поршня от ВМТ до НМТ, в любом месте по высоте, проводим полуокружность радиусом r. Из центра О в сторону НМТ откладываем поправку Брикса

OO₁ = rλ_ш/2=r²/(2L_ш),

а из точ­ки О₁, как из центра, проводим лучи через принятое число гра­дусов (на рисунке 5 через 15° ПКВ) до пересечения с окруж­ностью радиуса r. Проектируя полученные точки пересечения на ось V, получим давления, соответствующие этим углам поворота кривошипа. Отрезок по вертикали от оси V до индикаторной диаграммы будет соответствовать абсолютному давлению газов в цилиндре р_г, а отрезок между линией и индикаторной диа­граммой — избыточному давлению р_г-p₀.

Абсолютное значение силы давления газов на поршень

p_г=Р_гF_n, МН,

а относительное значение Р_г, МПа.

Движущая сила

Движущая сила является результирующей всех сил, действующих на поршень – силы давления газов в цилиндре Р_г, силы давления воздуха в подпоршневой полости Р_п.п, силы инерции ПДМ P_j, силы тяжести ПДМ Р_Т и равна их алгебраической сумме, МПа:

Р_дв=Р_г-Р_п.п+P_j+Р_Т,

где Р_п.п — сила атмосферного давления, если подпоршневая по­лость сообщается с картером, или давление продувочного воз­духа, если подпоршневая полость соединена с ресивером проду­вочного воздуха; Р_т=m_sg, где m — относительная величина поступа­тельно движущихся масс, кг/м²; g — ускорение свободного па­дения, м/с².

Движущую силу можно определить и графически. Для этого строят диаграмму сил давления газов Р_г = f(φ) и диаграмму сил инерции с обратным знаком — (-Р_j)=f(φ) и определяют ор­динаты между ними (рисунок 6). Силы тяжести ПДМ и противо­давление воздуха в подпоршневой полости — постоянные вели­чины и учитываются при построении.

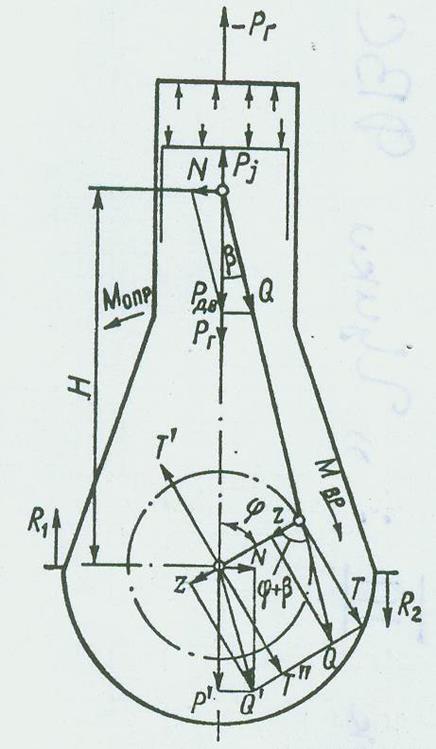
На рисунке 4 показано действие движущей силы в КШМ. Она приложена в центре поршневого пальца и действует вдоль оси цилиндра. Сила Р_дв раскладывается на составляющие: нормаль­ную силу, действующую перпендикулярно к оси цилиндра и при­жимающую поршень ко втулке N=P_двtgβ, и силу, действую­щую по оси шатуна

Q=P_дв/cosβ.

Силу Q переносим по линии ее действия в центр шатунной шейки и раскладываем на две составляющие: радиальную силу, действующую по кривошипу

Z=Qcos(φ+β)=P_двcos(φ+β)/cosβ

и касательную (тангенциальную) силу

Т= Qsin(φ+β)=P_двsin (φ+β)/cosβ.

Силы, действующие на КШМ, переменны по величине и на­правлению, поэтому для удобства анализа их представляют в виде графических зависимостей (см. рисунок 6), показывающих изменение сил по углу поворота кривошипа. Кривые периодиче­ские, с периодом 360° в двухтактных двигателях и 720° в четы­рехтактных. Силы считаются положительными, когда Рдв, Рj и Z направлены к центру вращения коленчатого вала, Т — на­правлена в сторону вращения коленчатого вала, а N — в сторо­ну, противоположную вращению. Угол β положителен, когда шатун отклонен в сторону вращения коленчатого вала.

Из точки О (см. рисунок 4) проведем два равных, но противо­положно направленных вектора Т’ и Т", параллельные и чис­ленно равные Т, и перенесем сюда же силу Z. Тогда пара сил T и Т’ образует момент, вращающий кривошип:

M_вр=Т_r = Р_двr*sin(φ+β)/соsβ,

а сумма оставшихся сил Т' и Z будет равна равнодействующей силе Q', которая нагружает подшипники.

Рисунок 6 - Диаграммы сил, действующих в КШМ одного цилиндра четырехтактного двигателя

Рг — сила давления газов в цилиндре; Р_j — сила инерции ПДМ: Р —движущая сила; Z — радиальная сила; N — нормальная сила; T — касательная сила

Сила Q' равна силе Q, действующей по шатуну, так как обе являются равнодействую­щими равных и одинаково направленных сил Z и Т, т. е.:

Q’=Q=P_дв/cosβ.

Вертикальная Р' и горизонтальная N' проекции силы Q' бу­дут соответственно равны:

Р’=Q'соsβ=Р_двсоsβ/соsβ=Р_дв;

N’=Q’sinβ=P_двsinβ/cosβ=P_двtgβ.

Следовательно, сила Р', действующая на остов двигателя в рамовом подшипнике в вертикальной плоскости, равна движу­щей силе Р_дв, а сила N', действующая на подшипник в горизон­тальной плоскости, равна нормальной силе N. Горизонтальные силы N и N' образуют пару сил с плечом H и создают перемен­ный по величине и направлению момент, называемый опрокиды­вающим. Опрокидывающий момент М_опр=NН действует в вер­тикальной поперечной плоскости в направлении, противопо­ложном действию вращающего момента, и уравновешивается внешним моментом реакций R₁ и R₂ на опорах.

Таким образом, результатом действия движущей силы являются: вращающий момент М_вр, приводящий в движение коленчатый вал; опрокидывающий момент М_опр, стремящийся опроки­нуть двигатель в сторону, противоположную действию М_вр, и сила инерции Р_j, стремящаяся приподнять или прижать двига­тель по отношению к судовому фундаменту. Все силы и момен­ты переменны по величине и направлению.

P’=P_дв;

P_дв-P_г=P_j – сила, действующая на фундамент двигателя.

Поправка Брикса

Важнейшим конструктивным параметром дизелей является постоянная КШМ:

λ=r/L_ш=1/5…1/3,5

где r – радиус кривошипа;

L – длина шатуна.

Перемещение поршня зависит от угла поворота КВ.

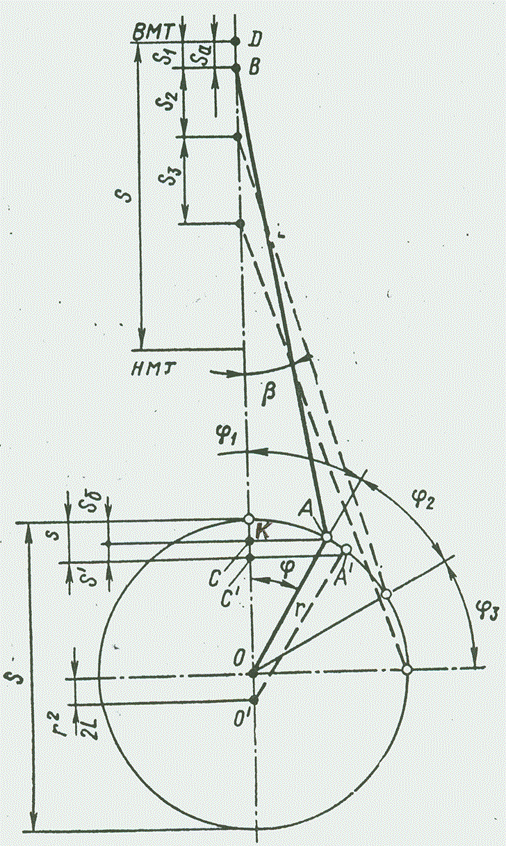
Из-за конечной длины шатуна L равным углам φ поворота КВ соответствуют неравные участки пути, проходимые поршнем (рисунок 7).

S(φ)=DB=OD-(OK+KB)

S(φ, β)=r+L-cosφ-Lcosβ (1)

При бесконечной длине шатуна β=0, и тогда:

S(φ)=r+L-r*cosφ-L=r-r*cosφ (2)

Из формул (1) и (2) можно получить значение поправки:

ОО’=S(φ, β)-S(φ)=r+L-r*cosφ-Lcosβ-r+r*cosφ=L-Lcosβ.

Максимальное значение поправки Брикса будет при 90° и 270° ПКВ:

S’=r²/2L=OO’.

Чтобы определить истинное мгновенное положение поршня, из центра О в сторону, противоположную цилиндру, откладывают эксцентриситет r²/2L. Из нового центра О’ проводят вектор O’A’ параллельно радиусу кривошипа. Проецируют точку A’ на вертикальную ось. Полученная точка будет соответствовать положению пальца поршня или центр подшипника поперечины крейцкопфа на ходе S.

Графический способ Брикса позволяет построить диаграмму перемещения поршня по углу φ.

Ускорение поршня достигает максимальных значений в ВМТ и НМТ, когда его скорость = 0. И наоборот, скорость поршня максимальна в тот момент, когда его ускорение = 0.

Лекция № 13.неравномерность вращения коленчатого вала. влияние числа оборотов, нагрузки и выключения цилиндров на равномерность вращения. определение результирующих сил инерции и их моментов. уравновешивание двигателей – 2 ЧАС.