Условия неискажённой передачи сигнала
Сигнал проходит через линейную цепь без искажений, если форма его на выходе не меняется, но могут измениться только его величина и появиться запаздывание по времени. Это возможно только в случае равномерной частотной характеристики и линейной фазовой характеристики цепи.
Справедливость такого условия можно показать и аналитически с помощью преобразования Фурье. Пусть на вход цепи подано напряжение UBX (t), имеющее спектральную функцию (или Фурье-образ) 
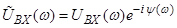. Выразим это напряжение с помощью интеграла Фурье:
Пусть цепь имеет коэффициент передачи с модулем K и с фазой, линейно растущей с частотой:
(3.52)
Тогда на выходе получим напряжение, определяемое выражением
или
Окончательно UВЫХ (t) = K UВХ (t – t0) . (3.53)
Действительно, напряжение на выходе имеет ту же форму, что и на входе, но изменено по величине в K раз и запаздывает по отношению к входному напряжению на время t0 . Для этого в (3.52) коэффициент передачи K должен быть постоянным, а фаза, как и написано в (3.52), должна линейно расти с частотой. Это нужно для того, чтобы гармоники с большей частотой запаздывали на большее число периодов.
Обычно передача сигнала (от "входа" к "выходу") может быть описана интегро-дифференциальным оператором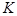 
:
Переходя к преобразованию Фурье, можно записать это соотношение в виде:
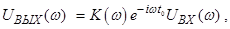
где K(ω) – комплексная рациональная функция (коэффициент передачи). Если K точно известно, то можно точновосстановить исходный сигнал, применив к полученному сигналу преобразование, обратное оператору .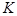
Часто удобнее (из-за технических ограничений) иметь дело не с самой функцией UВЫХ (t), а с рядом её дискретных отсчётов. Тогда естественно возникает вопрос, а эквивалентно ли представление функции в виде дискретных отсчётов самой функции? Здесь на помощь приходит теорема Котельникова. В зарубежной литературе она известна как теорема отсчётов – Sampling Theoremили теорема Найквиста – Nyquist-Shannon Theorem.
Теорема Котельникова (теорема отсчётов)
Зададим непрерывный сигнал U(t) набором отсчётов: Un = U(nΔ), где Δ — интервал дискретизации, 1/Δ — частота дискретизации (см. рис. 3.32).
Рис. 3.32. График функции U(t) и набор дискретных отсчётов Un c интервалом дискретизации Δ.
Это – наивысшая гармоника или наивысшая частота сплошного спектра сигнала.
Тогда справедлива теорема Котельникова (приводится без доказательства):
Если спектр сигнала ограничен и верхняя частота спектра меньше
то по дискретному набору Un можно точно восстановить исходный сигнал:
(3.54)
fc – частота Найквиста. Подчеркнём, что размерность fc – Гц.
В физическом эксперименте спектр любой функции всегда ограничен. Однако для математика функция, ограниченная по времени интервалом Т, имеет бесконечный спектр. В качестве примера можно привести формально неограниченный спектр прямоугольного сигнала, рассмотренный выше (см. рис. 3.11). На практике можно выбрать наивысшую частоту спектра fc так, чтобы “хвосты” спектра (содержащие частоты выше fс) содержали достаточно малую долю энергии сигнала. Величина малости определяется в каждом случае желаемой точностью воспроизведения сигнала.
Смысл теоремы в том, что наивысшая гармоника или наивысшая частота сплошного спектра сигнала должна быть задана двумя отсчётами.
Диоды
С точки зрения проводимости твёрдые вещества делятся на три категории: металлы, диэлектрики и полупроводники.
1. В металле есть свободные электроны, и поэтому их сопротивление мало.
2. В диэлектрике свободных электронов нет, все электроны распределены по атомам. Энергия отрыва (ионизации) электрона от атома велика. Естественным масштабом для оценки величины энергии ионизации является тепловая энергия, приходящаяся на колебательную степень свободы при T = 290K; kТ ~ 4·10–21 Дж = 0,03 эВ (k – постоянная Больцмана). Например, для алмаза энергия ионизации εАЛМАЗ ~ 5,4 эВ >> kТ.
3. В беспримесном полупроводнике электроны тоже распределены по атомам, но энергия ионизации меньше, например, для кремния Si εSi ~1,1 эВ, для галлия εGa ~ 0,67 эВ. Поскольку энергия отрыва электрона от атома всё-таки значительно больше kТ, то сопротивление беспримесных полупроводников тоже довольно значительно.
4. Несобственный полупроводник – это полупроводник, легированный примесями, атомы которых легко “расстаются” с электронами или присоединяют их. Различают n-тип (например, донор мышьяк As в Si) и р-тип (например, акцептор индий In в Si). Концентрация примесей обычно лежит в пределах ~ 1014 ... 1017 см-3. В 1 см3 Si порядка 0.5 1023 атомов. Энергия отрыва (или присоединения) мала, например, εAs ~ 0,01 ... 0,04 эВ ~ kТ.
N p
Рис. 4.1.
Кремний Si, легированный пятивалентным Или трёхвалентным индием In
мышьяком As (проводимость n-типа). (проводимость p-типа).
В данном случае перенос заряда В данном случае перенос заряда
осуществляется электронами. осуществляется дырками.
От количества свободных носителей и их подвижности зависит проводимость вещества. В чистых полупроводниковых веществах количество свободных носителей малó. Это и определяет низкую проводимость (или высокое удельное сопротивление) чистых полупроводников. При наличии примесей удельная проводимость может сильно изменяться. Например, у чистого германия проводимость около 2 Ом-1 м-1. При введении в германий всего 10-5 примеси мышьяка, удельная проводимость увеличивается до 2·104 Ом-1 м-1.
На использовании несобственных (легированных) полупроводников основана большая часть современной электроники. Простейший прибор из этого класса – полупроводниковый диод, с которого мы и начнём рассмотрение.
Дата добавления: 2019-04-03; просмотров: 1365;