Квантовая теория проводимости металлов.

Если в случае классической теории распределение электронов по энергиям определяются статистикой Максвелла-Больцмана (F_мб(Э)=Аe^(-Э/kT)), то в случае квантовой статистики распределение электронов по энергиям определяется распределением Ферми:

F(Э)=[1+e^(-Э_F^-Э)/кТ]^-1

Отличие данных статистик заключается в том, что в статистике Максвелла-Больцмана в каждом энергетическом состоянии может находиться несколько электронов, а в квантовой статистике, согласно принципу Паули в каждом энергетическом состоянии может находиться только один электрон. Вероятность заполнения энергетических уровней согласно квантовой статистики определяемая формулой, называется функцией Ферми, которая при нулевых температурах определяется следующим образом:

F(Э)=1, Э<=Э_r

F(Э)=0, Э>Э_r

Величина энергии Э представляет собой характеристическую энергию, которая показывает какую максимальную величину энергии может иметь электрон в металле при температуре абсолютного нуля. Эту характеристическую энергию называют уровнем Ферми (энергия Ферми). Распределение электронов в частично заполненной энергетической зоне и функция вероятности заполнения электронами энергетических уровней.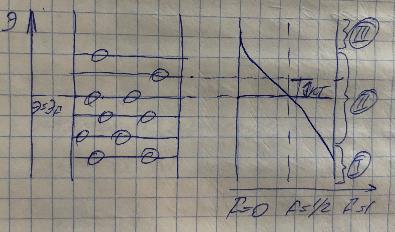

Вероятность заполнения уровней электронами максимальна для нижних энергетических уровней, при этом более высокие энергетические уровни остаются незаполненными. При сообщении веществу тепловой энергии величиной порядка КТ происходит переход электронов с низких энергетических уровней на более высокие. При этом уровни с энергией равной энергии Ферми заполняются с вероятностью 0,5.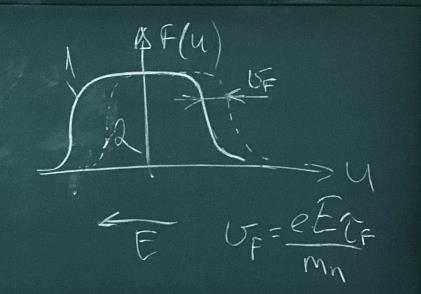

Лекция №4.

Распределение электронов по энергиям определяется как вероятностью заполнения электронами энергетических уровней, так и плотностью энергетических состояний в энергетической зоне. Величина концентрации электронов при нулевой температуре, определяется следующим соотношением:

n=int^э|₀N(Э)F(Э)dЭ=8pi/3(2m_n/h²)^3/2Э_r^3/2

F-вероятность заполнения энергетических уровней

Электроны в металле принимают участие в процессе электропроводности, при этом основной вклад вносят те электроны, которые имеют энергию, близкую к энергии Ферми. Электроны, находящиеся в металле под действием температуры могут изменять свое энергетическое состояние. Распределение электронов по энергиям при нулевой и ненулевой температуре: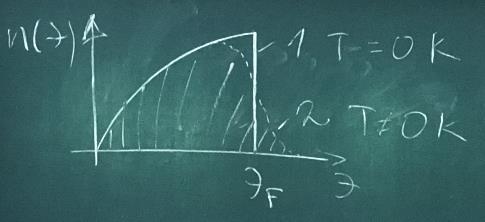

Под действием электрического поля происходит перераспределение электронов по скоростям, в результате этого происходит смещение графика распределения плотности электронов по скоростям против направления действия поля:

Приведенный на рисунке график распределения электронов по скоростям в отсутствии электрического поля обозначен цифрой 1, при воздействии электрического поля обозначен цифрой 2. Под действием электрического поля происходит смещение графика на величину скорости дрейфа. Величина скорости дрейфа при этом определяется соотношением:

v_F=eEt_F/m_n

Если подставить в выражение для времени свободного побега, то скорость дрейфа определяется выражением:

v_F=(eE/m_n)(l/u_F)

Выражение для плотности тока:

I=env_F

Проводимость металла, связанна с его концентрациейпрямопропорционально и определяется формулой:

j=e²nl/m_nu_F

Подставляем это выражение в формулу для концентрации электронов и получаем выражение для проводимости металла для случая квантовой теории проводимости:

mu_F²/2=Э_F=(3/8pi)^2/3n^2/3h²/2m_n

Температурная зависимость удельного сопротивления металлических проводников.

Движение свободных электронов в металле, с точки зрения волновой теории может рассматриваться как движение плоских волн. Длина этой волны определяется соотношением Де Бройля:

j=e²n^2/3l/n*(8pi/3)^1/3

Такая волна распространяется в периодическом поле кристаллической решетки без потерь энергии. В случае идеальной кристаллической решетки и при нулевых температурах длина свободного пробега стремится к бесконечности. В случае наличия в структуре кристаллической решетки точечных или протяженных дефектов, а так же при температурах отличных от температур абсолютного нуля, возникает рассеяние электронных волн на примесях и в узлах кристаллической решетки. Под действием тепловой энергии происходит колебание узлов кристаллической решетки. При отклонении их от положения равновесия, упругие силы межатомного взаимодействия стремятся вернуть их в исходное состояние. При этом действующая сила упругости должна соответствовать тепловой энергии:

lambda=h/m₀u=h/sqrt(2m₀Э)

Длина свободного пробега электронов связана с величиной упругого смещения атомов и температурой следующим соотношением:

1/2k_ynp(delta*a)²=kT

Частота колебания атомов в металле, определяет характеристической температурой, которую называют температурой Де Бая: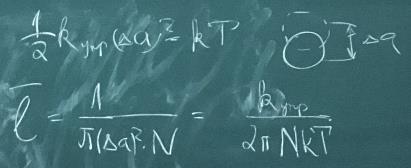

Величина сопротивления обратно пропорциональна проводимости и при температурах больше температуры Де Бая, определяется формулой: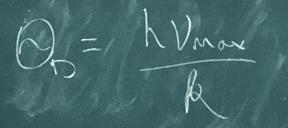

Температурная зависимость температурного сопротивления: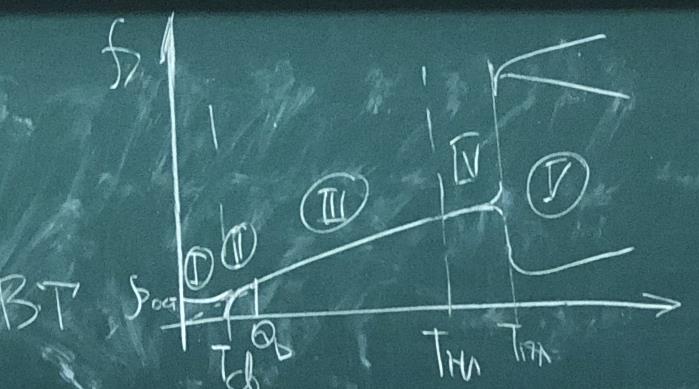

Участок 1 соответсвует области крайне низких температур. Теоретически в идеальном металле сопротивление на этом участке уходит в ноль, но у реальных металлов, в следствии наличия примесей и дефектов, сопротивление стремится к конечно сопротивлению - остаточное сопротивление ( ро остаточное). У ряда веществ наблюдается явление сверхпроводимости, при этом при температуре сверхпроводимости сопротивление обращается в ноль. Соответсвенно, на участке 2 график имеет нелинейный характер. При температурах свыше температуры Де Бая и до температур, близких к температурам плавления, зависимость имеет близкий к линейным характер. При температурах близких к температуре плавления происходит отклонение от линейного характера зависимости и при температуре плавления происходит резкое изменение величины предельного сопротивления. У большинства материалов при переходе в жидкое состояние, сопротивление скачкообразно возрастает в 1,5-2 раза. Однако у некоторых материалов может произойти уменьшение удельного сопротивления. Это происходит в веществах, обладающих сложной кристаллической структуры, которые при плавлении переходят в более простое состояние. Как правило, если объем при плавлении увеличивается, то возрастает и удельное сопротивление. В случае, если объем уменьшается, уменьшается и удельное сопротивление. Температурным коэффициентом удельного сопротивления называют относительное изменение удельного сопротивления при изменении температуры на 1 градус Кельвин: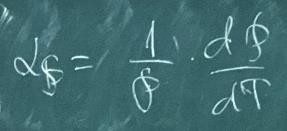

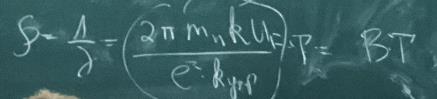
Величина удельного сопротивления при этом при некоторой температуре на участке линейной зависимости удельного сопротивления от температуры:

Лекция№5

Наличие в структуре кристаллической решетки дефектов и примесей изменяет структуру внутреннего потенциального поля в связи с чем происходит рассеяние электронов, на этих примесях и дефектах, даже при низких температурах, при которых отсутсвует рассеяние связанное с тепловыми колебаниями кристаллической решетки. Полное сопротивления проводника определяется суммой двух составляющих сопротивления обусловленного тепловыми колебаниями узлов кристаллической решетки и сопротивления обусловленного примесями и дефектами (ро ост). Закон об аддитивности сопротивления, называют правило Маттисена:

ро=ро_ост+ро_т

Наибольший вклад в величину остаточного сопротивления, вносит рассеяние на примесях. Примеси могут быть обусловлены как загрязнениями, так и внесением легирующих примесей для изменения свойств материала. Рассеяние на примесях ограничивает длину свободного пробега электронов, при этом итоговая длина свободного пробега определяется как длиной свободного пробега, определяемой тепловым рассеянием, так и длиной свободного пробега, определяемой рассеянием на примеси.

1/l=1/l_T+1/lп

В случае наличия рассеяния на примесях, полное сопротивление определяется выражением:

ро=(m_nu_F)/(e²n)S_nN_n+ро_Т

Влияние механических воздействий на удельное сопротивление металлов.

В случае наличия различного рода механических воздействий, ведущих к нарушению кристаллической решетки, так же происходит изменение в структурах потенциального поля, что приводит к изменению величины удельного сопротивления. В зависимости от характера внешнего механического воздействия, может происходит сжатие, растяжение, скручивание или пластическая деформация материала. В случае растяжения или упругого кручения материала присходит увеличение межатомных расстояний, при этом может увеличиваться температура амплитудных колебаний атомов и удельное сопротивление возрастает. При равномерном сжатии материала, происходит уменьшение межатомных расстояний, в связи с чем возрастают межатомные силы и амплитуда тепловых колебаний уменьшается, это приводит к уменьшению величины удельного сопротивления. Величина сопротивления материалов под влиянием внешних механических воздействий определяется формулой:

ро=ро₀(1±фи*дельта)

Ро - удельное сопротивление

Ро нулевое - удельное сопротивление в отсутвие механического воздействия

Фи - коэффициент уд сопротивления по давлению

фи=(1/ро)d ро/d дельта

При механической обработке материала, такой как пластическая деформация и наклеп, а так же при закалке происходит искажение внутренней структуры материала, что так же приводит к увеличению удельного сопротивления.