Значимость элемента в системе.

В 1969 г. проф. Бирнбаум определил надежностную значимость 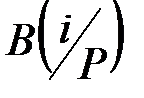элемента x_i в системе с монотонной структурой как частную производную:

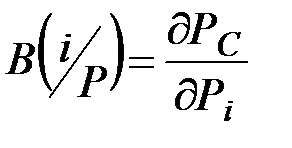(7.12)
где Р_C –– вероятность безотказной работы системы, зависящая, в частности, от надежности i-го элемента Р_i.

В том случае, когда значения P_i равнозначны, вычисляется так называемая структурная значимость B(i) i-го элемента:

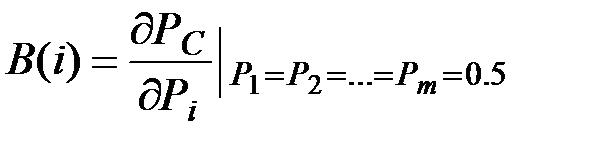(7.13)
т.е.

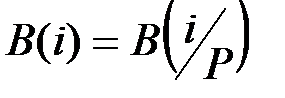(7.14)
с вероятностями безотказной работы всех элементов, равными 0.5.

Легко заметить, что надежностная значимость элемента соответствует скорости изменения надежности системы в зависимости от надежности данного элемента.

Структурная значимость элемента указывает на изменение надежности системы в случае замены данного элемента новым.

Рациональность использования логико-вероятностных методов можно продемонстрировать на следующем простом примере.

Пример 7.1.

Дана сложная структурная система (участок магистрального трубопровода), состоящая из пяти элементов х1, х2,..., х5, представленная схематично на рис. 7.1.

Рис. 7.1. Блок-схема развязки лупингов трубопроводной системы

Требуется определить надежность Р_С участка магистрального трубопровода от узла А до узла С, если известны вероятности безотказной работы (надежность) отдельных участков (Р1=0.8, Р2=0.85, Р3=0.9, Р4=0.75, Р5=0.7).

Решение.

Минимальные пути, сохраняющие работоспособность системы:

х1Ùх4, х2Ùх5, х1Ùх3Ùх5, х2Ùх3Ùх4 (7.15)
Следовательно, трубопроводная система сохраняет работоспособность при выполнении следующей логики:

(х1Ùх4)Ú(х2Ùх5)Ú(х1Ùх3Ùх5)Ú(х2Ùх3Ùх4) (7.16)
Тогда надежность системы, с учетом исходных значений вероятностей безотказной работы отдельных участков принимает вид:

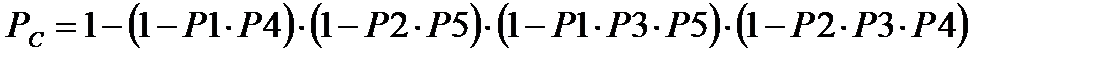(7.17)
Р_С = 0.96575.

При отсутствии элемента х3 итоговая надежность участка была бы равна:

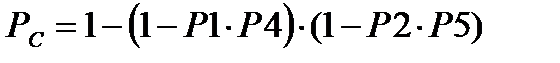=0.838 (7.18)
Определим значимость элементов, например, х1 и х3.

Надежностная значимость элемента х1:

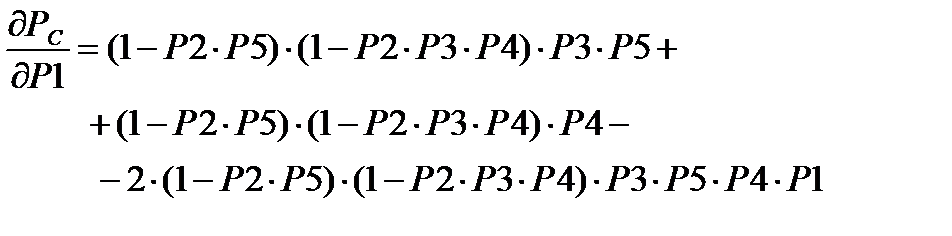(7.19)
Надежностная значимость элемента х₃:

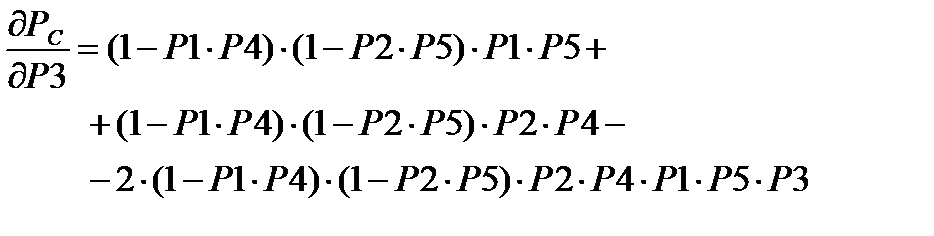(7.20)
После подстановки исходных данных по значениям надежности отдельных элементов, получим:

- надежностная значимость элемента х1 = 0.1077;

- надежностная значимость элемента х3 = 0.0898.

Для определения структурной значимости элементов подставим в полученные выражения значения вероятностей всех элементов, равные 0.5, получим структурную значимость элемента х1, равную 0.41016; структурную значимость элемента х3, равную 0.2461.

На основании проведенных расчетов можно сделать вывод о том, что в надежности системы элемент х3 в сравнении с элементом х1 играет при данных значениях надежности остальных элементов не столь существенную роль, а в структурной значимости элементов системы роль элемента х3 существенно менее значима в сравнении с элементом х1.

Аналогичные расчеты по оценке значимости можно произвести для всех элементов рассматриваемой системы.

Решение примера 7.1 в системе Matlab.

PC=(1-(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4))

syms P1 P2 P3 P4 P5; Символьное дифференцирование.

PC1=diff((1-(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4)),P1)

PC2=diff((1-(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4)),P2)

PC3=diff((1-(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4)),P3)

PC4=diff((1-(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4)),P4)

PC5=diff((1-(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4)),P5)

Определение надежностной значимости элементов системы.

P1=0.8;P2=0.85;P3=0.9;P4=0.75;P5=0.7; Исходные данные.

PC11 =P4*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*P3*P5*(1-P2*P3*P4);

PC12 =(1-P1*P4)*P5*(1-P1*P3*P5)*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*P3*P4;

PC13 =(1-P1*P4)*(1-P2*P5)*P1*P5*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*P2*P4;

PC14 =P1*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*P2*P3;

PC15 =(1-P1*P4)*P2*(1-P1*P3*P5)*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*P1*P3*(1-P2*P3*P4);

Определение структурной значимости элементов системы.

P1=0.5;P2=0.5;P3=0.5;P4=0.5;P5=0.5; Новые значения надежности элементов.

PC21 =P4*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*P3*P5*(1-P2*P3*P4)

PC22 =(1-P1*P4)*P5*(1-P1*P3*P5)*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*P3*P4

PC23 =(1-P1*P4)*(1-P2*P5)*P1*P5*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*P2*P4

PC24 =P1*(1-P2*P5)*(1-P1*P3*P5)*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*(1-P1*P3*P5)*P2*P3

PC25 =(1-P1*P4)*P2*(1-P1*P3*P5)*(1-P2*P3*P4)+(1-P1*P4)*(1-P2*P5)*P1*P3*(1-P2*P3*P4)