Основные логические операции.

Конъюнкциядвух высказываний А и В обозначается А Ù В (читается: А и В). Иногда вместо знака логического умножения используют символ «·» или между перемножаемыми высказываниями знак вообще отсутствует.

Конъюнкция А Ù В двух высказываний представляет собой сложное высказывание, которое истинно тогда и только тогда, когда истинны составляющие его высказывания А и В.

Значение истинности логического произведения А Ù В определяется следующими соотношениями:

0 Ù 0 = 0; 0 Ù 1 = 0; 1 Ù 0 = 0; 1 Ù 1 = 1. (7.1)

Дизъюнкция двух высказываний А и В обозначается А Ú В (читается А или В). Часто применяется матричная форма обозначения дизъюнкции:

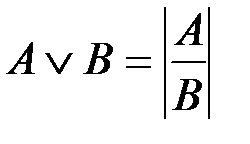(7.2)
Значение истинности логического сложения А Ú В определяется следующими соотношениями:

0 Ú 0 = 0; 0 Ú 1 = 1; 1 Ú 0 = 1; 1 Ú 1 = 1 (7.3)
Дизъюнкция двух высказываний является сложным высказыванием, которое ложно тогда и только тогда, когда оба высказывания ложны.

Отрицание высказываний А обозначается А¢ (иногда 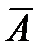) читается: не А. Значение истинности высказывания А определяется соотношениями:

1¢=0; 0¢=1 (7.4)

Таким образом, отрицанием высказывания А является сложное высказывание А¢, которое ложно, когда А истинно, и истинно, когда А ложно.

Приведенные выше логические операции могут быть выражены друг через друга. Преобразование логических выражений выполняется по определенным правилам.

Правила для одной переменной.

А Ù 1 = А;

А Ù 0 = 0;

А Ù А = А;

А Ù А¢ = 0;

А Ú 1 = 1;

А Ú 0 = А;

А Ú А = А;

А Ú А¢ =1;

А¢¢ = А;

А¢¢¢= А¢;

Приведенные выше правила легко доказываются подстановкой вместо А единицы или нуля. Следствием является закон тавтологии:

АÙАÙ…А = А;

АÚАÚ…А = А.

В отличие от обычной алгебры в алгебре логики умножение переменной самой на себя или приведение подобных членов осуществляется согласно перечисленным правилам без появления показателей степени или коэффициентов.

Для двух и трех переменных функции конъюнкции и дизъюнкции обладают свойствами, аналогичными свойствам операций умножения и сложения. Можно убедиться, что для этих функций действует сочетательный (или ассоциативный) закон, а также переместительный (или коммутативный) закон:

АÙ(ВÙС)=(АÙВ)ÙС=АÙВÙС (7.5)

АÚ(ВÚС)=(АÚВ)ÚС=АÚВÚС (7.6)

АÙВ=ВÙА (7.7)

АÚВ=ВÚА (7.8)
Для логического умножения и логического сложения сочетательного и переместительного законов выражения, в которые входят конъюнкции и дизъюнкции, можно писать без скобок. При этом связь посредством знака Ù считается более тесной, нежели связь посредством знака Ú. Тем самым в алгебре логики «старшие» действия выполняются раньше «младших», что позволяет вместо (АÙВ)ÚС иметь более упрощенную запись АÙВÚС. В алгебре логики имеет место распределительный (или дистрибутивный) закон конъюнкции относительно дизъюнкции, а также распределительный закон дизъюнкции относительно конъюнкции:

АÙ(ВÚС)=(АÙВ)Ú(АÙС) (7.9)

АÚ(ВÙС)=(АÚВ)Ù(АÚС) (7.10)
Заметим, что в обычной алгебре последнее правило не имеет места:

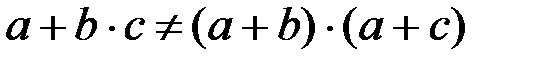(7.11)

Заметим также, что все отмеченные законы обладают свойством «симметрии». Закон двойственности в алгебре логики позволяет заменять отрицание конъюнкции дизъюнкцией отрицаний.

Приведем несколько полезных определений, [2].

Кратчайший путьопасного (безопасного) функционирования представляет собой такую конъюнкцию инициирующих событий, ни одну из компонент которых нельзя изъять, не нарушив опасного (безопасного) функционирования системы.

Минимальное сечение предотвращения опасности представляет собой такую конъюнкцию из отрицаний инициирующих событий, ни одну из компонент которой нельзя изъять, не нарушив условия безопасного функционирования системы.