Надежность системы с задержанным восстановлением

Рассмотрим более общий и более реальный случай, когда на ремонт или восстановление отказавшего устройства требуется конечное время.

Допустим, что техническая система состоит из одного устройства, находящегося под действием простейшего потока отказов с интенсивностью l. Отказавшее устройство немедленно начинает восстанавливаться (ремонтироваться). Поток восстановлений тоже простейший с интенсивностью m. Запас средств или деталей для ремонта считается неограниченным.

Требуется определить:

надежность системы как вероятность P₀(t) того, что в момент t система будет находиться в работающем состоянии;

предельное значение надежности P системы как вероятность того, что в произвольный достаточно удаленный от начала работы системы момент времени система будет работать;

вероятность того, что до определенного момента времени t система будет работать безотказно, т.е. не будет иметь ни одного перерыва на выполнение ремонта.

Для ответа на поставленные вопросы рассмотрим размеченный граф состояний системы, представленный на рис. 8.4 и составленный по правилам, изложенным во втором разделе настоящего пособия.

Рис. 8.4. Размеченный граф состояний ремонтируемой системы

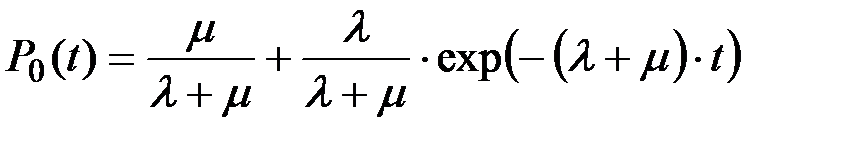
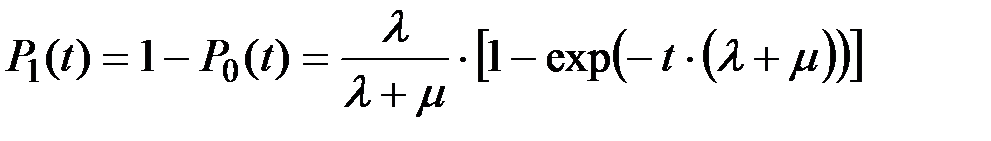(8.7)
где P₀(t) –– вероятность нахождения системы в состоянии S₀ (рабочее состояние); P₁(t) –– вероятность нахождения системы в состоянии S₁ (состояние ремонта).

Вероятность того, что рассматриваемая техническая система будет работать в произвольный момент t (надежность системы) равна:

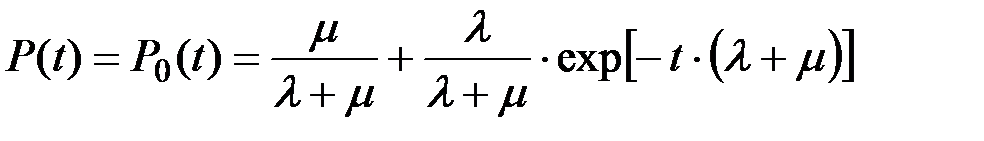(8.8)
При стремлении t к бесконечности эта надежность стремится к предельному значению:

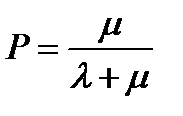(8.10)
т.е. она равна относительной доле интенсивности потока восстановлений в суммарной интенсивности потоков восстановлений и отказов.

Вероятность 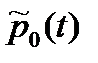того, что до момента t не произойдет ни одного отказа, определим следующим образом. Предположим, что ремонта отказавшего устройства нет, т.е. граф состояний имеет вид, изображенный на рис.8.5.

Рис. 8.5. Граф состояний системы без восстановлений

Искомая вероятность 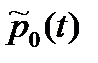будет равна вероятности того, что система (рис. 8.5) к моменту t будет находиться в состоянии S₀. Эта вероятность может быть получена решением дифференциального уравнения:

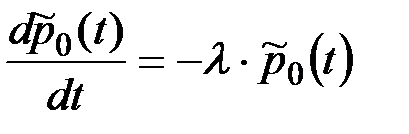(8.11)

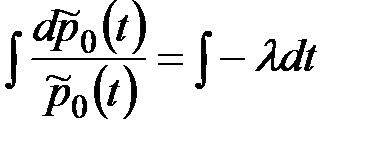
Откуда:

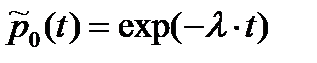(8.12)
Таким образом вероятность 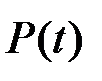равна:

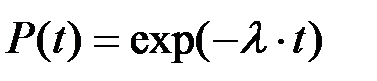(8.13)
Ответы на поставленные выше вопросы получены на базе аппарата теории систем массового обслуживания, изложенного во втором разделе.

Продолжаем усложнение задачи и допустим, что техническая система состоит из нескольких устройств общим числом m+1. Каждое устройство находится под действием простейшего потока отказов с интенсивностью l. При отказе любого устройства система останавливается и начинает ремонтироваться. Во время восстановления системы отказы устройств происходить не могут. Интенсивность потока восстановлений равна m. Все потоки простейшие.

Требуется определить:

надежность P(t) системы как вероятность того, что в момент t система будет в рабочем состоянии;

предельную надежность р системы;

вероятность 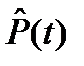того, что до момента t отказов вообще не будет.

Для ответа на поставленные вопросы обратимся к размеченному графу состояний системы, изображенному на рис. 8.6.

Рис. 8.6. Размеченный граф состояний системы с несколькими однотипными восстанавливаемыми устройствами при отказе системы равносильном отказу одного (любого) устройства

Решение поставленной задачи базируется на том обстоятельстве, что система может находиться только в двух состояниях: рабочем (S₀) или нерабочем (S₁). Граф состояний системы, изображенный на рис. 8.6. отличается только тем, что интенсивность потока отказов составляет (m+1)×l. Отсюда, на основании решения предыдущей задачи, имеем:

-вероятность того, что в момент времени t система находится в рабочем состоянии:

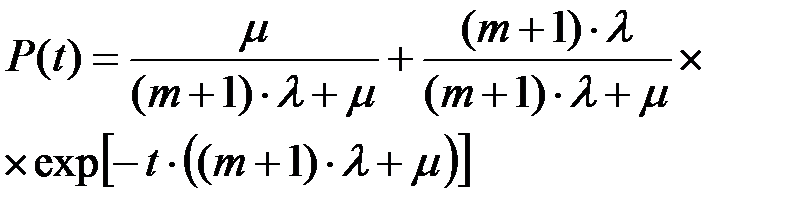(8.14)
-предельная вероятность нахождения системы в рабочем состоянии:

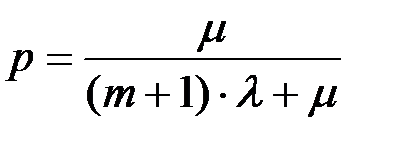(8.15)
-вероятность того, что до момента времени t не произойдет ни одного отказа системы:

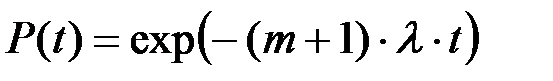(8.16)
Если предположить, что в сложной технической системе при отказе одного устройства остальные продолжают работать и система при отказе одного устройства не прекращает своего функционирования, то картина будет иной и более сложной.