Определение надежности сложной восстанавливаемой системы

Для сокращения записи будем считать, что система состоит из общего числа m устройств (ранее всегда было (m+1)), каждое из которых находится под действием потока отказов (неисправностей) с интенсивностью l. При отказе устройства оно немедленно начинает восстанавливаться, остальные устройства при этом продолжают работать, обеспечивая рабочее состояние системы. Интенсивность потока восстановлений устройства (независимо от числа одновременно восстанавливаемых устройств) равна m.

Требуется определить:

вероятность P(t) того, что в момент времени t все устройства будут исправными;

предельную вероятность того же события;

среднее число исправных устройств при t ® ¥.

Решение поставленной задачи требует составления размеченного графа состояний (рис. 8.7).

Состояния системы будем нумеровать по числу неисправных устройств:

S₀ –– все устройства исправны;

S₁ –– одно устройство ремонтируется, остальные исправны;

……………………………………………………………………..

S_k –– k устройств ремонтируются, m-k –– исправны;

……………………………………………………………………..

S_m –– все m устройств находятся в ремонте.

Рис. 8.7. Размеченный граф сложной технической системы

Для рассматриваемого графа система дифференциальных уравнений имеет вид:

…………

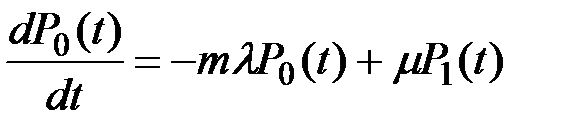
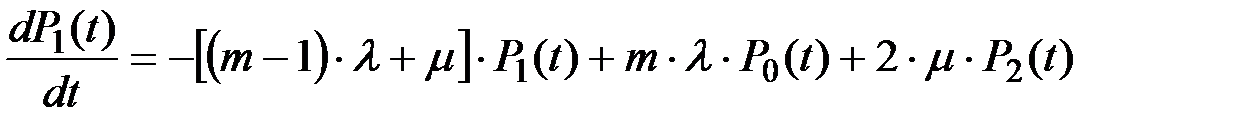
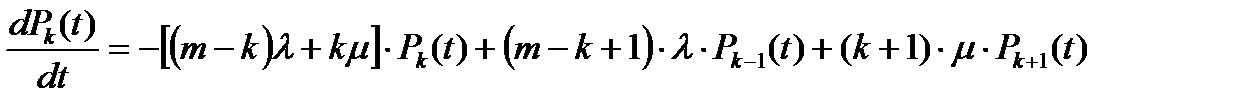
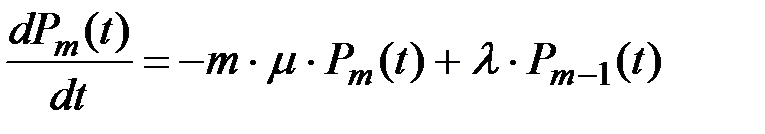(8.17)

Плюс условие полной группы событий:

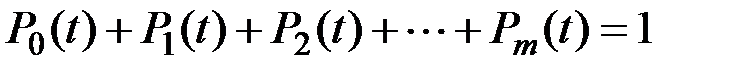(8.18)
Вероятность P(t) того, что все элементы в момент t будут исправны, есть не что иное, как вероятность P₀(t), которую получим, интегрируя представленную систему дифференциальных уравнений при следующих начальных условиях:

При t = 0, P₁(0)=P₂(0)=…=P_m(0)=0; Р₀(0)=1.

Предельные вероятности состояний находим по аналогии с решением, приведенным в разделе 2 (системы массового обслуживания), полагая :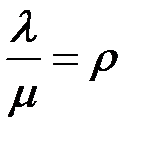

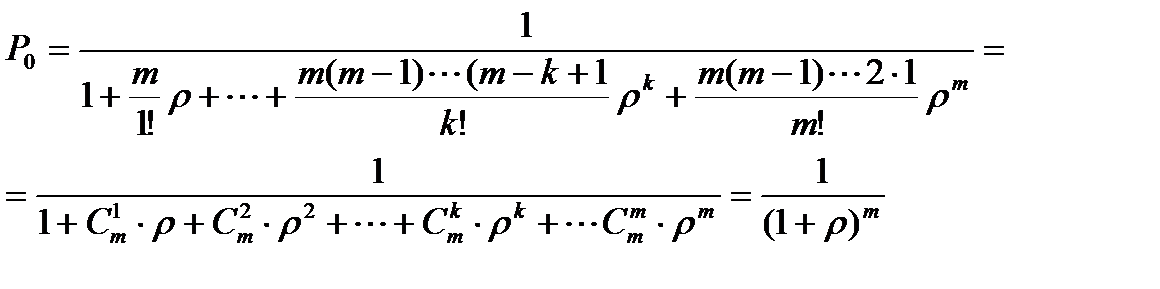(8.19)
Искомая предельная вероятность того, что в установившемся режиме при стремлении величины t к бесконечности все устройства сохранят работоспособность, и будет определяться выражением (8.19), т.е. Р=Р₀.

Среднее число 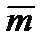исправно работающих устройств будет равно числу устройств m, умноженному на вероятность того, что отдельно взятое устройство исправно. Эта вероятность 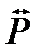(при t®¥) равна:

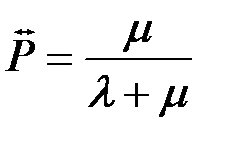(8.20)
откуда, среднее число исправно работающих устройств равно:

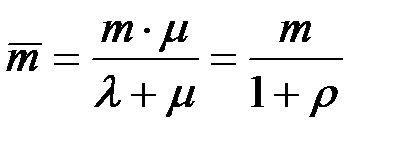(8.21)
Рассмотренные задачи и примеры показывают, что аппарат, применяемый для анализа надежности технических систем весьма совпадает с аппаратом теории массового обслуживания, и исследование процессов, протекающих в системах с отказывающими устройствами, при определенных условиях может быть проведено методами непрерывных марковских цепей. Для этого необходимо, чтобы потоки событий, переводящие устройства из состояния в состояние, были хотя бы приближенно пуассоновскими. Эти потоки не обязательно должны быть стационарными, но такими, чтобы интенсивности потоков событий не зависели от случайных моментов переходов системы из одного состояния в другое.

На этом основании разработаны практические алгоритмы оценки различных технических систем с восстановлением [8].