Метод золотого сечения

Метод определения интервала, содержащего минимум

Для практического применения методоводномерного поиска необходимо знать начальный интервал 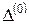, в котором целевая функция 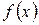унимодальна и который содержит ее минимум. Этот интервал может быть получен, например, с помощью последовательной серии нескольких возрастающих шагов по независимой переменной х.

Пусть заданы начальное значение 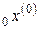и начальный шаг h.

Шаг 1). Если 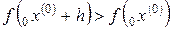, то h = ‒ h, k = 0, перейти к шагу 2.

Шаг 2). Вычислить , .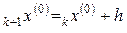

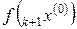Шаг 3). Если 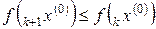, то h = 2 h, вернуться к шагу 2 при k = k + 1.

Если 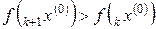, то обозначить , .

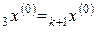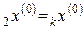
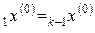Тогда начальный отрезок 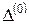, включающий минимум 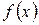равен .

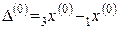Метод золотого сечения

Здесь используются две дроби Л. Фибоначч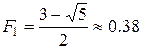и и 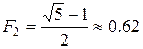, которые соответствуют разбиению отрезка на две части, которое известно как «золотое сечение» 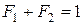, , 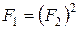, 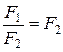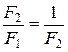(отношение длины всего отрезка к большей части равно отношению большей части к меньшей).

Обозначим k = 0, , , .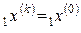

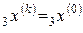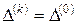Шаг 1). Вычислить , .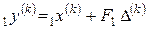

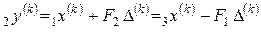Шаг 2). Если 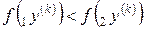, то , , .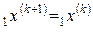

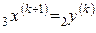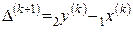Если 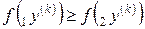, то , , .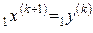

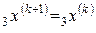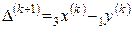Вернуться к шагу 1 при k = k + 1.

Условие выхода 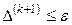, решение задачи одномерной минимизации

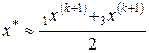. (1.2.1)

Для большей точности каждый раз определяются две новые точки, а не одна как при делении интервала пополам. В этом случае ошибки округления при вычислениях не могут привести к потере интервала, содержащего минимум.

1.3. Метод ДСК(алгоритм Дэвиса, Свенна и Кэмпи)

При одномерном поиске по алгоритму ДСК проводятся возрастающие по величине шаги до тех пор, пока не будет пройден минимум, а затем выполняется одноразовая квадратичная интерполяция.

Обозначим последние три значения, найденные при определении интервала, содержащего минимум , .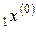

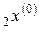
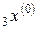Тогда

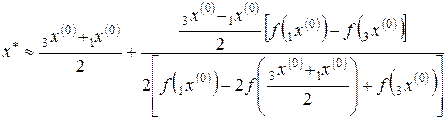. (1.3.1)

Пример 1.2.1÷1.3.1 Решение задачи одномерной минимизации методами «золотого сечения» и ДСК

Пусть .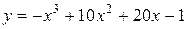

Локальный минимум, ближайший к 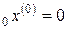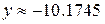при .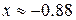

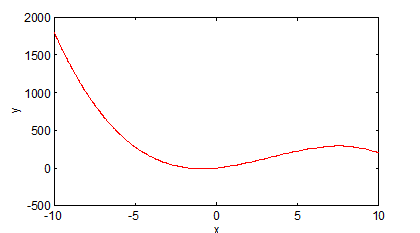
Найдем эти значения методами одномерного поиска.

Пусть h = 0.01, , .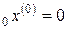

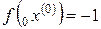Вначале определим интервал, содержащий минимум.

, ,

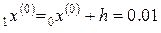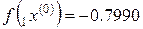h = ‒ h = ‒ 0.01.

, ,

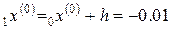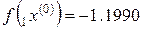h = ‒ 0.02, , ,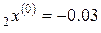

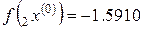h = ‒ 0.04, , ,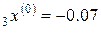

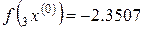h = ‒ 0.08, , ,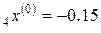

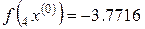h = ‒ 0.16, , ,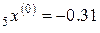

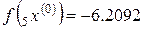h = ‒ 0.32, , ,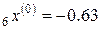

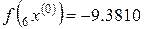h = ‒ 0.64, , ,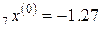

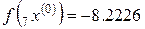Тогда , , .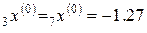

, , .

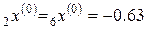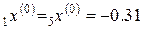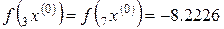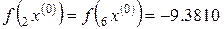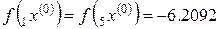По методу ДСК , .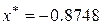

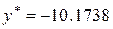По методу «золотого сечения» , .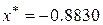

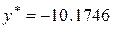d = ‒ 0.9600 через 29 шагов d = ‒ 9.1544e ‒ 007.