Функция распределения местной напряженности поля

Реальный электроизоляционный материал отличается от идеального диэлектрика наличием неоднородностей: дефектов структуры, примесей, наполнителей, пластификаторов и т.д.

На связи, расположенные вблизи неоднородностей, действует повышенная напряженность электрического поля. Повышение напряженности поля в диэлектрике учитывается коэффициентом β. Очевидно, разрыв связей прежде всего происходит в той области материала, где β имеет наибольшее значение. Параметр β обусловлен формой, размерами и характеристиками неоднородностей.

Неоднородности в материалах распределены случайным образом. В процессе изготовления материала и изделия из него происходят разделение и коагуляция неоднородностей. Это приводит к тому, что форма и размеры неоднородностей являются случайными, а, следовательно, случайным будет и параметр β. Так как в уравнение "кривой жизни" электрической изоляции входит наибольшее значение β, то необходимо для оценки вероятности безотказной работы и сроков службы электроизоляционной конструкции найти функцию распределения наибольших величин β.

Для вывода функции распределения наибольших величин β сделаем следующие предположения:

1) элементарные неоднородности имеют сферическую форму с одинаковым радиусом сфер;

2) элементарные неоднородности по объему распределены по закону случайной смеси;

3) расположенные рядом в одну линию неоднородности образуют эллипсоид вращения.

Первое и второе предположение являются очевидными. Действительно, исследования показывают, что такие неоднородности, как точечные дефекты, примеси, распределены по законам случайной смеси. При введении наполнителя наилучшим смешением считается условие, что введенные компоненты будут подчиняться законам случайной смеси.

В реальном теле встречаются неоднородности, которые имеют разнообразную форму и достаточно сильно отличаются по размерам. Однако любую реальную неоднородность всегда можно представить как комбинацию элементарных, имеющих сферическую форму и одинаковые размеры.

Третье предположение не является строго корректным, так как в действительности рядом расположенные сферы не являются эллипсоидом вращения. Однако такая замена не будет давать большой погрешности.

Сделанные предположения позволяют построить физико-математическую модель неоднородного диэлектрика. Концентрацию неоднородности в диэлектрике при равномерном их распределении получим из формулы:

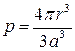(2.28)

где r – радиус сферической неоднородности; a – расстояние между центрами неоднородностей.

В реальном диэлектрике неоднородности распределены случайным образом, а не равномерно. В этом случае концентрация неоднородностей равна отношению объема, занятого неоднородностями, к объему тела, т.е. формула справедлива и при случайном их распределении при условии, что a является средним расстоянием.

Рис. 8. Схема неоднородного диэлектрика

Рассмотрим (рис. 8) в электрической изоляции элементарный цилиндр диаметром, равным среднему расстоянию между неоднородностями а, и длиной, равной межэлектродному расстоянию l. Вероятность попадания неоднородности в цилиндр равна р. Условная вероятность размещения центра неоднородности, попавшей в цилиндр, на его оси найдем как геометрическую вероятность:

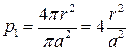(2.29)

Вероятность попадания неоднородности в цилиндр и размещения ее центра на оси получим по теореме умножения вероятностей:

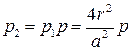(2.30)

Определив из формулы концентрации неоднородности отношение r/a и подставив его в p₂, получим:

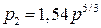(2.31)

Функция распределения y (число рядом расположенных неоднородностей):

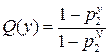(2.32)

где N = l/2r – число неоднородностей, которые максимально могут разместиться на оси, или число мест на оси, которые могут занять неоднородности.

Наибольшая напряженность поля имеет место у неоднородностей, вытянутых в направлении электрического поля, т.е. при максимальных значениях y. Пусть имеется образец, состоящий из n ячеек. Значение y в каждой ячейке – величина случайная, подчиняющаяся функции распределения. Функцию распределения наибольших значений y получим из условия одновременного выполнения событий: в каждой ячейке y меньше некоторого наперед заданного значения, т.е. F(y)=Q(y₁ 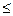y)Q(y₂ 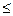y)…Q(y_n 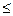y), где y₁, y₂, …, y_n – значения y в первой, второй, n-й ячейке соответственно.

Так как функция распределения Q(y) для всех ячеек одинакова, то

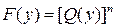(2.33)

Число ячеек в образце толщиной l и площадью электродов S

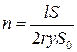(2.34)

где S₀ = πa²/4 – площадь поперечного сечения элементарного цилиндра.

Подставляя Q(y) и n, получаем:

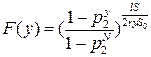(2.35)

Обозначим V₀=2rS₀, тогда

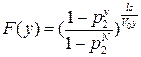(2.36)

Относительная проводимость неоднородности в общем виде:

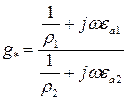(2.37)

где ρ₁ и ρ₂ – удельные объемные сопротивления неоднородности и окружающего диэлектрика соответственно; ε_a1 и ε_a2 – абсолютные диэлектрические проницаемости неоднородности и окружающего диэлектрика соответственно; ω – круговая частота переменного тока.

Для переменного напряжения введем tgδ=1/ρωε_a. Тогда получим:

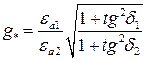(2.38)

где tgδ₁ и tgδ₂ – тангенс угла диэлектрических потерь неоднородности и окружающего диэлектрика.

Найдем y:

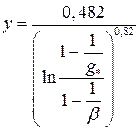(2.39)

где β – коэффициент неоднородности электроизоляционного материала, который в однородном поле, создаваемом электродами, равен отношению E_max/E_ср.

Функцию распределения вероятностей наибольшей напряженности поля (наибольшего значения β) получим, подставив y:

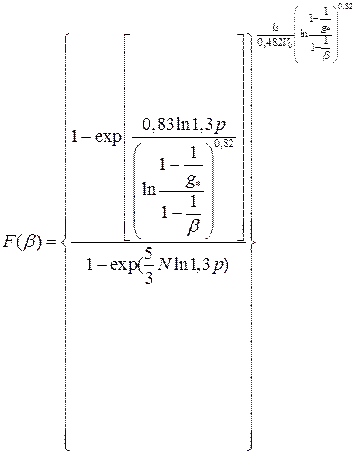(2.40)

Функция справедлива для однородного поля. В неоднородном поле наибольшая местная напряженность будет определяться неравномерностью поля и неоднородностью электроизоляционного материала. В неоднородном электрическом поле наибольшая напряженность поля, создаваемого электродной системой, всегда имеет место у электрода с меньшим радиусом кривизны. Очевидно, расположение неоднородности у электрода с меньшим радиусом кривизны приведет к появлению большей местной напряженности поля, чем ее появление в других участках изоляции. Чтобы распространить функцию на случаи неоднородного поля, введем эквивалентную толщину изоляции. Эквивалентная толщина изоляции в неоднородном поле равна такой толщине изоляции в однородном поле, при которой максимальная напряженность неоднородного поля равна средней однородного, если приложенное напряжение одинаково в обоих случаях. Учитывая введенный ранее коэффициент неоднородности поля η, находим:

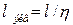(2.41)

У электрода с меньшим радиусом кривизны напряженность поля будет в η раз больше средней.