Законы распределения случайных величин, используемые в теории надежности

Использовать надежностные характеристики объекта, заданные в виде таблицы весьма неудобно. Поэтому по результатам эксперимента подбирают аналитическую формулу, которая наиболее удачно подходит в данном случае, и определяют коэффициенты этой формулы. Наиболее типичные формулы называются законами распределения случайных величин. Рассмотрим наиболее распространенные законы.

Показательное (экспоненциальное) распределение.

Показательное распределение характерно тем, что интенсивность отказов постоянна 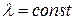. Отсюда

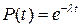(1.28)

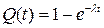(1.29)

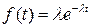(1.30)

Примерный вид соответствующих кривых показан на рис. 2.

Рис. 2. Примерный вид кривых

при экспоненциальном распределении

Показательное распределение применяется на практике очень широко.

Усеченное нормальное распределение.

При нормальном (гауссовом) распределении случайной величины ось абсцисс имеет протяженность от -∞ до +∞. Поскольку время t не может быть отрицательной величиной, в теории надежности используется усеченное нормальное распределение.

Усеченным нормальным распределением случайной величины называется распределение, получаемое из нормального при ограничении интервала возможных значений этой величины.

Основными параметрами для нормального распределения являются T – среднее значение наработки на отказ и σ_t – среднеквадратическое отклонение.

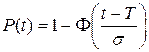(1.31)

где Φ(u) – нормированная функция нормального распределения.

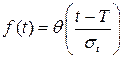(1.32)

Значения Φ(u) и θ(u) определяются из справочника.

Примерный вид соответствующих кривых представлен на рис. 3.

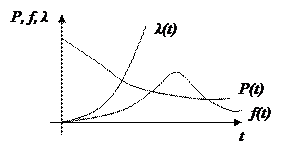
Рис. 3. Примерный вид кривых при усеченном нормальном распределении

Нормальное распределение может использоваться при исследовании надежности объектов, отказы которых обусловлены действием какого-то одного доминирующего фактора.

Распределение Вейбулла

Основными параметрами распределения Вейбулла являются λ₀ - масштаб кривой по оси абсцисс и α – острота и асимметрия распределения. Обычно берут 1≤α≤2.

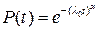(1.33)

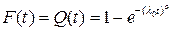(1.34)

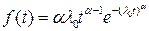(1.35)

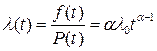(1.36)

При α = 1 распределение Вейбулла переходит в экспоненциальное. Примерный вид соответствующих кривых дан на рис. 4.

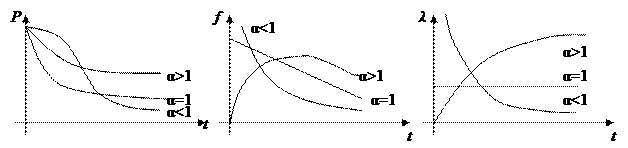
Рис.4. Примерный вид кривых при распределении Вейбулла

Гамма-распределение.

Гамма-распределение имеет те же параметры, что и распределение Вейбулла, α и λ₀. Форма кривых P(t), f(t) и λ(t) также аналогична форме кривых при распределении Вейбулла.

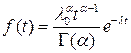(1.37)

Γ(α) – гамма-функция, для которой имеются соответствующие таблицы. Однако гамма-распределение чаще всего описывает распределение времени безотказной работы резервированных изделий, при этом параметр α равен суммарному количеству объектов, поэтому чаще всего α – целое число. При целом α:

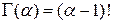(1.38)

Тогда

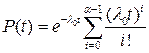(1.39)

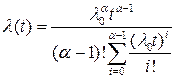(1.40)

При α = 1 гамма-распределение переходит в экспоненциальное, а при больших α – в нормальное.