Невосстанавливаемые элементы и системы

Технические системы, их подсистемы и элементы систем могут работать в режиме, когда восстановление со стороны ремонтного персонала возможно, и в режиме, когда это невозможно либо нецелесообразно. Поэтому для восстанавливаемых и для невосстанавливаемых элементов и систем применяются различные показатели надежности и различные методы расчета надежности.

Показатели надежности невосстанавливаемых объектов:

1) Вероятность безотказной работы объекта P(t) выражает вероятность того, что невосстанавливаемый объект не откажет к моменту времени t.

Если F(t) – функция наработки на отказ, то P(t)=1-F(t).

P(t) обладает следующими свойствами:

а) P(0)=1 (предполагается, что до начала работы изделие является безусловно работоспособным);

б) 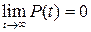(предполагается, что объект не может сохранить свою работоспособность неограниченно долго);

в) Если t₂ > t₁, то P(t₂) ≤ P(t₁) (вероятность безотказной работы – функция невозрастающая).

Статистически определить 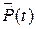по результатам испытаний можно с помощью следующей формулы:

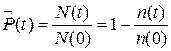(1.9)

где N(t) – число исправных объектов в момент времени t, n(t) – число отказавших объектов к моменту времени t.

2) Вероятность безотказной работы объекта в интервале времени от t₁ до t₂:

(1.10)

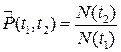(1.11)

3) Вероятность отказа Q(t) выражает вероятность того, что невосстанавливаемый объект откажет к моменту времени t:

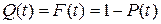(1.12)

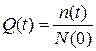(1.13)

4) Вероятность отказа в интервале времени от t₁ до t₂:

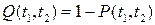(1.14)

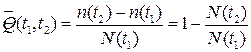(1.15)

5) Плотность распределения отказов f(t) определяет вероятность возникновения отказа в момент времени t:

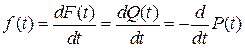(1.16)

Статистическая оценка 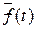производится за интервал времени Δt, так как функция f(t) является дифференциальной:

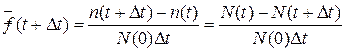(1.17)

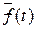можно рассматривать как среднее число отказов в единицу времени непосредственно после момента t, приходящееся на один элемент из всех объектов, поставленных на испытания.

В связи с этим f(t) на практике обычно называют частотой отказов.

6) Интенсивность отказов λ(t) определяет вероятность возникновения отказа в момент времени t с учетом числа объектов, работоспособных к моменту времени t:

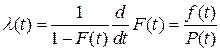(1.18)

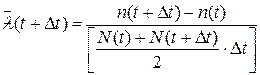(1.19)

можно рассматривать как среднее число отказов в единицу времени непосредственно после момента t, приходящееся на один элемент, из всех объектов, продолжающих работать к этому моменту t. Отсюда видно, что λ(t) характеризует надежность объекта в момент t более полно, чем f(t), этим и объясняется более широкое применение на практике этого показателя.

Если известна плотность вероятности отказов, то нетрудно определить вероятность отказов или вероятность безотказной работы:

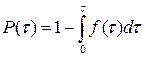(1.20)

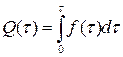(1.21)

Если известна λ(τ), то

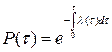(1.22)

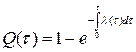(1.23)

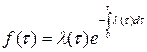(1.24)

7) Среднее время наработки на отказ T определяется как математическое ожидание времени до отказа:

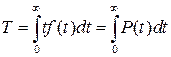(1.24)

(1.25)

8) Дисперсия наработки до отказа Dt. Средняя наработка до отказа является точечной оценкой и не говорит ничего о характере распределения времени до отказа. Две совершенно различные функции P₁(t) и P₂(t) (рис. 1) могут характеризоваться одинаковыми значениями средней наработки на отказ

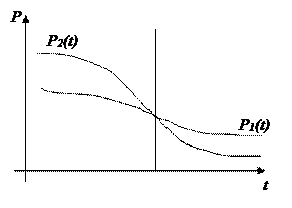Рис. 1. Пример различной дисперсии

T₁=T₂. Чтобы различать такие случаи наряду с показателем T, используется показатель Dt – дисперсия наработки до отказа или его корень квадратный σ_t – среднеквадратическое отклонение наработки до отказа:

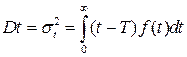(1.26)

Дисперсия характеризует величину разброса наработки относительно среднего значения:

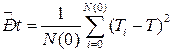(1.27)

Где T_i – время до отказа i-го объекта.