Для линейной зависимости векторов необходимо и достаточно,чтобы один из них был линейной комбинацией остальных.

Доказательство.

Пусть векторы 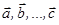линейно зависимы, тогда существуют числа 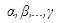, одновременно не равные нулю, такие, что 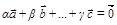. Для определенности можно считать, что 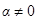, но тогда , что и требовалось доказать.

Легко доказать: любые два коллинеарных вектора линейно зависимы, а два неколлинеарных вектора линейно независимы.

Доказательство начнём с первого утверждения.

Пусть векторы 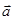и 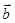коллинеарны. Покажем, что они линейно зависимы. Действительно, если они коллинеарны, то они отличаются друг от друга только на числовой множитель, т.е. 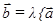, следовательно 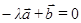. Поскольку полученная линейная комбинация явно нетривиальная и равна «0», то векторы 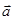и 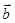линейно зависимы.

Рассмотрим теперь два неколлинеарных векторы 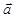и 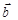. Докажем, что они линейно независимы. Доказательство построим от противного.

Предположим, что они линейно зависимы. Тогда должна существовать нетривиальная линейная комбинация 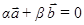. Предположим, что 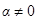, тогда 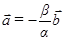. Полученное равенство означает, что векторы 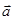и 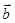коллинеарны вопреки нашему исходному предположению.

Аналогично можно доказать: любые три компланарных вектора линейно зависимы, а три некомпланарных вектора линейно независимы.