Теорема. Пусть дан базис ,тогда любой вектор в пространстве может быть представлен и притом единственным образом в виде , где –некоторые числа.
Доказательство. Докажем вначале существование таких чисел.
Совместим начала всех векторов 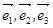 и
и 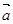 в точке O и проведем через конец вектора
в точке O и проведем через конец вектора 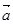 плоскость, параллельную плоскости O,
плоскость, параллельную плоскости O, 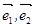 (рис. 4.1). Построим новые векторы
(рис. 4.1). Построим новые векторы 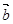 и
и  так, что
так, что 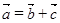 , а
, а  и
и 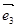 были коллинеарны, тогда в силу коллинеарности векторов
были коллинеарны, тогда в силу коллинеарности векторов 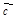 и
и 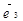 имеем
имеем 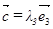 . Перенеся затем начало вектора
. Перенеся затем начало вектора 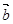 в точку O , получим
в точку O , получим 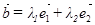 и, следовательно,
и, следовательно, 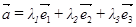 что доказывает существование разложения.
что доказывает существование разложения.
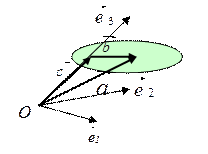

Рис. 4.1 Разложения вектора 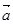 по базису
по базису 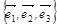
Докажем единственность разложения по базису. Пусть мы имеем 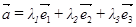 и допустим, что существует другая тройка чисел
и допустим, что существует другая тройка чисел 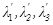 таких, что
таких, что 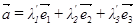
Вычитая почленно эти равенства, получаем
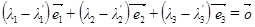
где в силу сделанного предположения о не единственности разложения
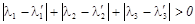
Но полученное неравенство означает, что линейная комбинация
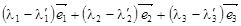
нетривиальна, векторы 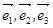 линейно зависимы и, следовательно, не могут быть базисом в силу определения 2.4.1. Полученное противоречие доказывает единственность разложения.
линейно зависимы и, следовательно, не могут быть базисом в силу определения 2.4.1. Полученное противоречие доказывает единственность разложения.
Определение 4.6 Числа 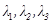 – коэффициенты в разложении
– коэффициенты в разложении 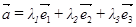 – называются координатами вектора
– называются координатами вектора 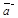 в базисе
в базисе 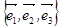
Для сокращенной записи координатного разложения вектора 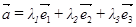 используются формы:
используются формы: 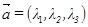 или
или 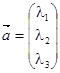
Наконец, если вектор 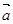 в базисе
в базисе 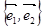 на плоскости может быть представлен как
на плоскости может быть представлен как 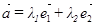 , то его координатная запись имеет вид
, то его координатная запись имеет вид 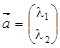 .
.
Отметим, что указание координат вектора вовсе не фиксирует жестко его положение в пространстве. Координаты вектора лишь отражают его аналитическую связь с базисом, задающим систему координат. В данном случае мы рассматриваем свободные векторы, и любой вектор, полученный из данного путем параллельного переноса, будет иметь те же координаты.
Пример 4.1. Даны векторы 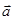 = (1; 2; 3),
= (1; 2; 3), 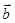 = (-1; 0; 3),
= (-1; 0; 3), 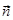 = (2; 1; -1) и
= (2; 1; -1) и 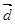 = (3; 2; 2) в некотором базисе. Показать, что векторы
= (3; 2; 2) в некотором базисе. Показать, что векторы 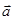 ,
, 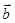 и
и 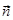 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 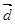 в этом базисе.
в этом базисе.
Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
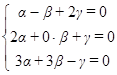 линейно независимы.
линейно независимы.
Тогда 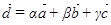 .
.
Это условие выполняется, если определитель матрицы системы отличен от нуля.
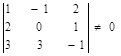
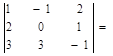
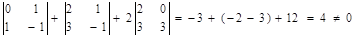
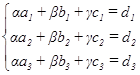 Для решения этой системы воспользуемся методом Крамера.
Для решения этой системы воспользуемся методом Крамера.
D1 = 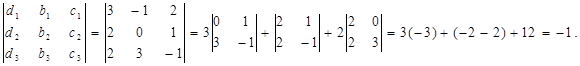
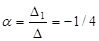 ;
;
D2 = 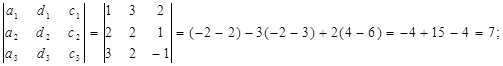
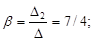
D3 = 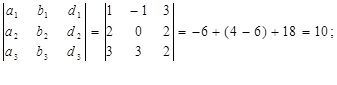
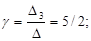
Таким образом, координаты вектора 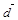 в базисе
в базисе 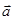 ,
, 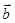 ,
, 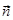 :
: 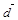 { -1/4, 7/4, 5/2}.
{ -1/4, 7/4, 5/2}.
Введение базиса в пространстве и на плоскости позволяет поставить в соответствие каждому вектору 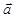 упорядоченную тройку (пару) чисел – его координаты. Это, в свою очередь, позволяет установить связь между геометрическими объектами и числами, делает возможным аналитически описывать и исследовать положение и движение физических объектов.
упорядоченную тройку (пару) чисел – его координаты. Это, в свою очередь, позволяет установить связь между геометрическими объектами и числами, делает возможным аналитически описывать и исследовать положение и движение физических объектов.
Базис еще называют репером пространства. Параллельным переносом приведем векторы, образующие базис, к общему началу. Совокупность точки и базиса называютсистемой координат.
С каждым из базисных векторов можно связать одинаково ориентированную с ним ось. Эти оси и образуют в общем случае так называемую аффинную систему координат (рис. 4.2).
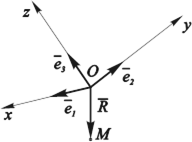
Рис. 4.2. Аффинная система координат.
Если векторы, образующие базис единичны и попарно перпендикулярны, то система координат называется прямоугольной, а базис ортонормированным.
Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.
Впервые прямоугольную систему координат ввел Рене Декартв своей работе «Рассуждение о методе» в 1637году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлеруже в XVIII веке.
Дата добавления: 2018-11-30; просмотров: 1532;
