Векторная и скалярная проекции вектора

Проектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. Проекцией вектора 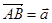на плоскость σназывается вектор 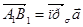(рис. 2.2), заключенный между основаниями перпендикуляров, опущенных из его начала и конца на плоскость σ.

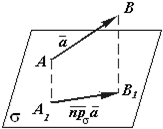
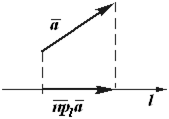
Рис.2.1 Векторная проекция вектора на ось. Рис.2.2. Векторная проекция вектора на плоскость

Наряду с векторной проекцией вектора на ось l , существует и скалярная проекция , которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси l , и равна величине, ей противоположной, если векторная проекция и ось l имеют противоположную ориентацию. Скалярную проекцию будем обозначать: .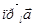

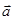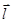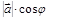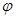Определение 2.2Проекцией вектора на ось называется число, равное , где - угол наклона вектора 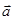к оси ( )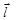

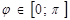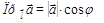
Свойства:

1) 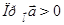,если ;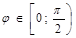

2) 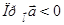,если ;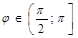

3) 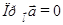, если ;

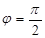4) .

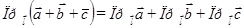Замечание1. Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора. При решении же задач необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» – в соответствии с установленным смыслом.

Замечание2. Необходимо иметь в виду, что определение множества векторов 2.1допускает их дальнейшую, более тонкую дифференциацию. Например, в некоторых физических и технических приложениях различают векторы полярные и аксиальные. К первым относятся, например, векторы скорости, силы, напряженности электрического поля; ко вторым – векторы момента силы, напряженности магнитного поля. Кроме того, в механике векторы подразделяются на свободные, скользящие и закрепленные, в зависимости от той роли, которую играет точка их приложения.