Physico-chemical features of nanostructured materials

Properties of nanostructured materials

Objectives:

Ø To analyze physico-chemical properties of nanostructured materials.

Ø To explain size effect of nanoparticles on the chemical and thermodynamic properties.

Physico-chemical features of nanostructured materials

Physical-chemistry of solid-state nanostructures seems to be a bridge between such traditional areas as atomic physics, where the properties of individual atoms are studied, and the physical chemistry of the concentrated state, in which solid materials are studied and their number of atoms is practically infinite.

In fact, a nanostructure is a very small fragment of a solid. However, it turns out that at such small dimensions, the properties of nanostructures are very different from those of bulk materials.

As you already know, the task of nanotechnology is the creation of low-dimensional systems with the sizes of structural elements from fractions to several tens of nanometers.

The usual physico-chemical concepts, including the concepts of "composition-properties", "structure-function" are supplemented in this case by the terms "size", "self-organization".

Nanoscience studies:

- the properties of isolated nanoparticles

- the location of atoms inside a nanoscale formed from nanoparticles

The relative stability of individual parts of the nanostructure is dependent on:

ü kinetic and

ü thermodynamic factors

In general, nanoparticles can be considered as intermediate formations between atoms on the one hand, and a solid state on the other. Nanoparticles and nanosystems have many physico-chemical properties that were not previously observed in solids.

What are the main reasons for this affirmation?

There are two main factors influencing the formation of the properties of nanosystems:

- a change in the thermodynamic state of nanosystems in comparison with the classical one and

- the appearance of quantum-size effects with a decrease in the characteristic sizes of structural elements.

Theoretical and experimental studies of the thermodynamics of small particles show that the particle size is an active thermodynamic variable that determines the state of the system together with other thermodynamic variables. Because of their small size, they have a high interface. Therefore, nanoparticles of less than 10 nm in size have:

- excess energy and

- high physicochemical activity.

The excess energy of such objects is primarily determined by the nature of the bonds of atoms, which are in the surface and atoms that are near the surface.

The formation of nanoparticles from atoms is accompanied by two processes:

- the formation of metallic nuclei of different sizes and

- the interaction between the particles, which facilitates the creation of ensembles representing nanostructures from them.

These new systems have very different properties than the conventional materials and the particle size plays a very important role in the explanation of these properties.

As example, the particle size can be regarded as a kind of equivalent temperature, and in this case the value of the Gibbs potential will differ from the standard values of the massive phase (Fig. 1).

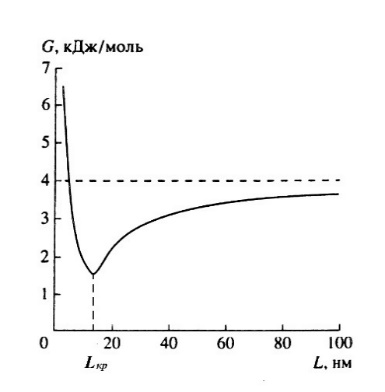
Fig.1. Change in the free Gibbs energy (G) of a binary nanostructured alloy with an average concentration of 5% of the crystallite size (L). For a conventional crystal, G = 4 kJ/mol

Many researchers have found a significant increase in the electrical resistivity of nanocrystalline Cu, Pd, Fe, Ni, and various alloys with a decrease in grain size. One of the relationships connecting the resistivity ρ of the nanocrystalline material with the grain size D is:

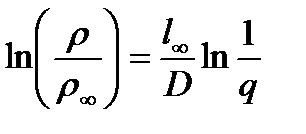
Where:

- ρ∞ is the electrical resistivity of a coarse grain substance;

- l∞ is the mean free path of electrons in a single crystal;

- q is the coefficient of electron scattering during the transition of grain boundaries.

Since the scattering coefficient is 0<q<1, it follows from expression (1) that as the grain size decreases, the resistance of the nanocrystalline material should increase. The main reason for increasing the electrical resistivity is the scattering of electrons at the grain boundaries.

Other important direction in the investigation of nanomaterials is the study of mechanical properties, such as: hardness, strength, ductility, elasticity, etc. Experimental studies of the mechanical properties of nanomaterials have shown that the tensile strength and hardness of many metals (Pd, Cu, Ag, Ni, etc.) are much higher than in the corresponding coarse analogues.

The increase in hardness and strength with decreasing grain size to a certain critical size is practically characteristic of all crystals. This follows from the well-known Hall-Petch equation that the strength of the metal depends inversely on the average grain size:

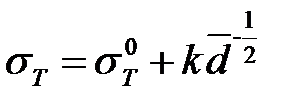(2)

Where:

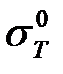- is strength of a single crystal

- k is a coefficient of strength (specific for each material)

- d is an average grain size

This relation is performed for range of values up to 1 μm. The values obtained for σ_T by extrapolations in a region of size‹10 nm show that the strength is 2-3 times larger than those for traditional materials.

Reduction of the grain size will cause the material to become stronger. On the other hand, grain size reduction also increases the hardness of the metal.

There are some experimental results obtained on nanocrystals. They show that they are much stronger than coarse analogues. Nanophase Cu, Pd, Fe with grain size ~ 5 nm, showed hardness values 2-5 times higher than in samples with the usual grain size, as we can see in the figure 2.

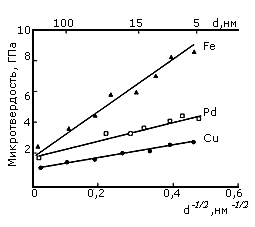
Fig. 2. Effect of grain size (d) on the micro hardness of metals.

At the same time, the growth of hardness and strength in nanomaterials is practically independent of the way they are produced. For example, in nanocrystals obtained by crystallization from an amorphous state, an increase in hardness was also observed in both single-component and multicomponent nanomaterials.

The hardness increases with decreasing of size not only for metals, but also for ceramics. However, the size of the grain to which hardening occurs, depends on several factors and its nature is not entirely clear. Usually the Hall-Petch relation (2) is satisfied for many nanomaterials only up to a certain grain size, and at its lower values reverse effects are observed: hardness (strength) decreases with decreasing grain size (Fig. 3).

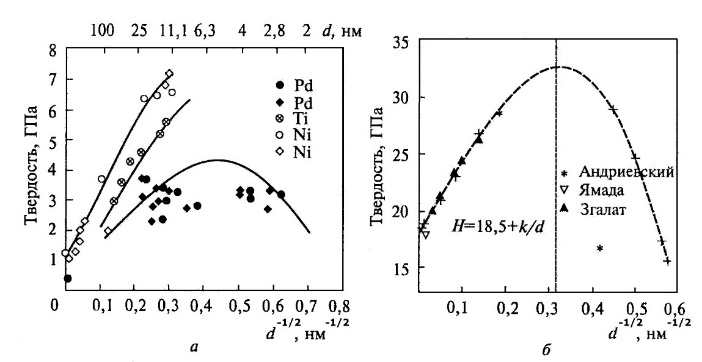
Fig. 3. Dependence of the microhardness of various materials on the grain size: metals (a); ceramics (b).

Now, it is not entirely clear whether the hardness values obtained for real compacted nanomaterials correspond to perfectly dense nanosystems.

The behavior of nanomaterials in this case can be masked by contributions from the residual porosity - cracks and other defects that arise in nanomaterials due to the peculiarities of the methods for obtaining them.

The determining role in the anomalies of the mechanical properties of nanomaterials is, probably, the grain boundaries. The nature of the interfaces in general and with respect to nanomaterials, continues to be the subject of discussions. In the simplest case, a nanocrystalline material consisting of atoms of one kind contains two components that differ in structure: ordered grains (crystallites) with a size of 5-20 nm and intergranular boundaries up to 1.0 nm. In Fig. 4 presents the simplest two-dimensional model of nanostructure with nanocrystallites of different size and orientation.

Fig.4. Two-dimensional model of nanocrystalline material. Nanocrystallites with different orientations are depicted in the form of black circles, interphase boundaries - in the form of light circles.

An important factor determining the mechanical behavior of nanomaterials is internal stresses. They are always present in nanomaterials because of the large number of closely spaced grain boundaries. In addition, internal stresses can arise due to the peculiarities of the methods for obtaining nanomaterials. The presence of high internal stresses in nanocrystals also leads to a change in the atomic structure of nanomaterials, and at the same time it can cause other changes in the nanostructures.

Let´s consider in more detail dimensional effects in Nanochemistry.

The study of experimental data and reactions of atoms, clusters and nanoparticles of various elements of the periodic system allows us to formulate the following definition:

Dimensional effects in chemistry is a phenomenon that manifests itself in a qualitative change in physicochemical properties and reactivity, depending on the number of atoms or molecules in a particle of matter, occurring in an interval of less than 100 atomic-molecular diameters.

Pазмерные эффекты в химии – это явление, выражающееся в качественном изменении физико-химических свойств и реакционной способности в зависимости от количества атомов или молекул в частице вещества, происходящее в интервале менее 100 атомно-молекулярных диаметров.

The manifestation of size effects is one of the main differences of nanochemistry from chemical transformations under the usual reaction conditions. There are two types of size effects - internal, and external. The internal one is associated with specific changes in the volume and surface properties of both individual particles and the ensembles obtained because of their self-organization. The external effect is a dimensionally dependent response to an external field or the action of forces independent of the internal effect. The study of internal dimensional effects is aimed on the studying of the electronic and structural properties of clusters, and the effect on chemical activity, the ionization potential, the binding energy between atoms in a particle and between particles, and the crystallographic structure.

As we already know, the melting point can also be considered as a function of the particle size and its geometry. The dependence of the spatial arrangement of electronic levels on the size of nanoparticles is called the quantum-size effect.

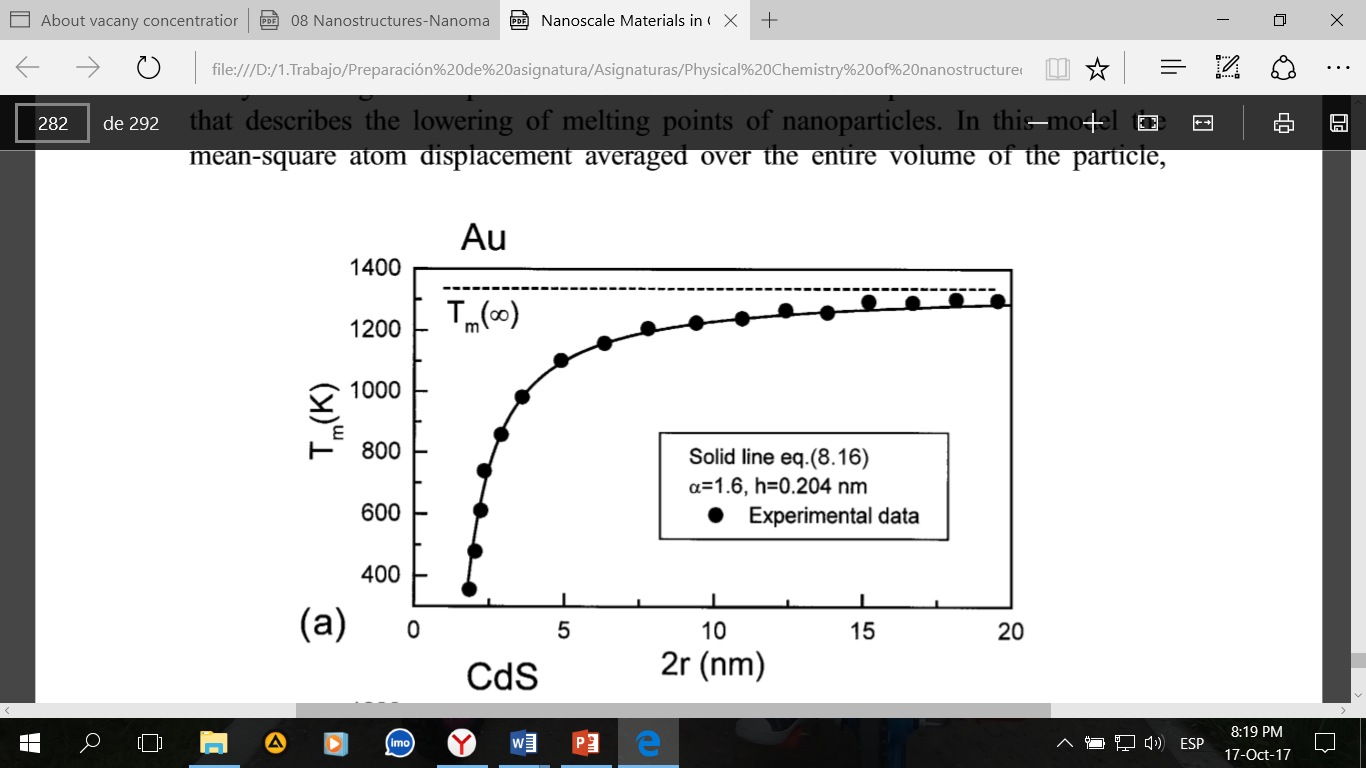
The change in the melting temperature of metals as a function of particle size is one of the first dimensional effects that attracted the attention of scientists. With a decrease in size, the melting point can decrease by several hundred degrees, and for gold, for example, a compact metal melts at 1340 K, and nanoparticles of 2 nm size melt already at 340 K.

The transition from the solid phase to the liquid phase is associated with the melting point, when the crystalline structure of the solid phase disappears and is replaced by less ordered state of the liquid. A significant decrease in the melting point with a decrease in particle size may affect their activity and selectivity. Indeed, as experiments have shown, nanoparticles have increased chemical and catalytic activity.

The dependence of the melting temperature on the size of the metal particles is considered based on two models:

- one of them uses the representations of thermodynamics,

- the other - the vibrations of atoms.

From the standpoint of thermodynamics, the lowering of the melting points is in general explained by the fact that the surface energy increases with a decreasing size. Some assumptions are applied to develop a model or approximation to predict a size dependence of melting temperature of nanoparticles. The starting assumption is made of the simultaneous existence of a solid particle, of a liquid particle having the same mass, and of a vapor phase. The equilibrium conditions are then described based on these assumptions. The relationship between the melting points of a bulk material, T_b and a particle, T_m is given as follow:

Where r_s, is the radius of the particle, ∆H is the molar latent heat of fusion, Υ and ρ are surface energy and density, respectively. It should be noted that the above theoretical description is based on classical thermodynamic considerations, in which the system dimensions are infinite, which is obviously inconsistent with the subject of nanoparticles in the range of a few nanometers. It should also be noted that the model is developed based on the assumption that nanoparticles all have the equilibrium and perfect crystals. However, model is consistent with the experimental data.

The dependence of the melting temperature of metal nanoparticles on the size is also explained based on the criteria proposed by Lindemann: the vibrations of atoms.

As the temperature increases, amplitude of oscillation increases and at the certain temperature these oscillations are strong enough to break the crystal structure of a solid and cause melting. Surface atoms are not as strongly bound and can experience higher amplitude vibrations at a given temperature than atoms within the volume of the particles. This effect can be described by the following ratio:

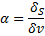
Where 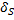are atoms on the surface and 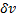, atoms inside the nanoparticle. The values of 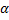is typically between 2 to 4. Since nanoparticle have very large fraction on the surface (for example for spherical particle of 3 nm, about 50 % of the atoms are on the surface) their oscillations will significantly affect the Lindemann criteria.

This circumstance was used to describe the dependence of the melting temperature of nanoparticles on their size without the representations of thermodynamics. A model that considers a decrease in temperature with a decrease in the size of nanoparticles is developed by Shi. To describe the properties of nanoparticles, an equation is proposed:

Where Tm (r) and Tm (∞) are the melting points of a nanocrystal and a compact metal, respectively, K; h corresponds to the height of the monolayer of atoms in the crystal structure and r is the size of the nanoparticle.

Equation can be used to predict a decrease in the melting temperature of nanocrystals if the parameter 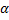is known, which is usually determined from the corresponding experimental data.

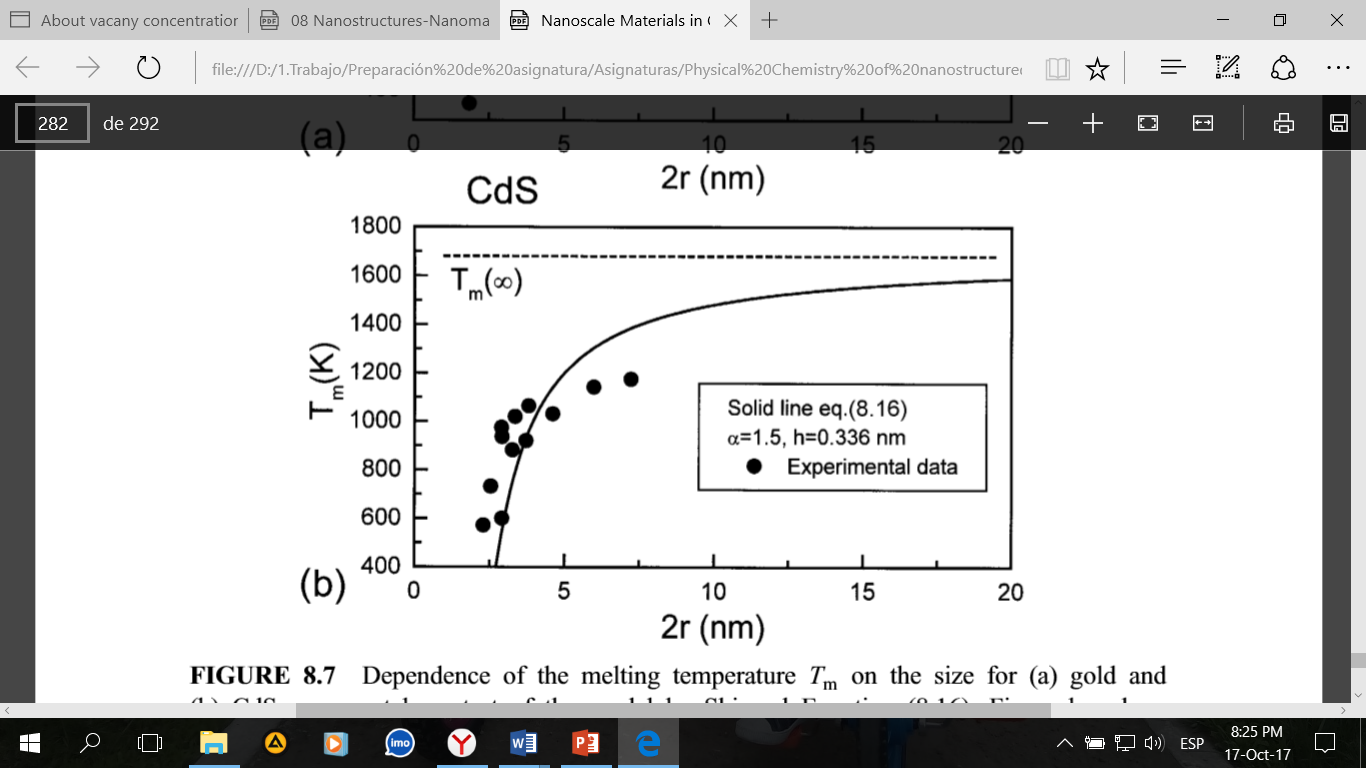
Some nanocrystalline particles are materials in which one metal is included in the other. In such cases, the melting point of a particle can both decrease and increase in comparison with a compact material with a change in the particle size.

Summarizing, we can say that free metal nanoparticles always show a decrease in the melting point with a decrease in the size of the nanoparticle. For systems consisting of metal matrices with included nanoparticles of another metal, both a decrease and an increase in the melting temperature with decreasing particle size are possible.

Control questions

1. What are the main factors that influence in the properties of nanomaterials?.

2. Mention the steps of nanostructures formation.

3. Why is important the particle size.

4. Explain the behavior of the mechanical properties with decreasing of size in nanostructured materials.

5. Describe the size effect on the melting point of nanostructured materials.

6. Analyze the models that explain the dependence of melting point on the size of metallic nanoparticles.