Some thermodynamic features of nanoparticles

Thermodynamic features of nanoparticles. The adsorption properties of nanoparticles and nanomaterials.

Objectives:

Ø To analyze the influence of size factor on the chemical equilibrium.

Ø To discuss the adsorption properties, as very important factor for the application of nanoparticles and nanomaterials.

During the last activity, we were talking about metal based nanoparticles, that as you know they are composed mainly, by metal atoms. Also, we were talking about the properties of these group nanomaterials and studied the influence of some thermodynamic variables on the properties of these nanoparticles.

One of the most important variable is the size of the particle. What is the dependence between the size and properties of nanoparticles??

In fact, with decreasing of the size properties like, electrical resistivity, strength, hardness increase their values and make possible the application of nanomaterials in many areas of the industry. We can mention the important role of these material in nanoelectronic industry.

Today, we will continue studying the size effect in the properties of nanocrystals

Some thermodynamic features of nanoparticles

There is a significant number of atoms on the surface of nanoparticles. When their size decreases, then the number of atoms on the surface increases. As a result the new properties of these materials are very different than classical materials (massive, concentrated, bulk, conventional material)

Accordingly, to this situation, the surface energy nanocrystal also increases with increasing of the number of atoms on the surface. In other words, the surface energy increases with decreasing of particle size.

With the change of the size of nanoparticles we can see that some thermodynamic parameters are associated with this variation. Concentration of vacancies increases with decreasing of size.

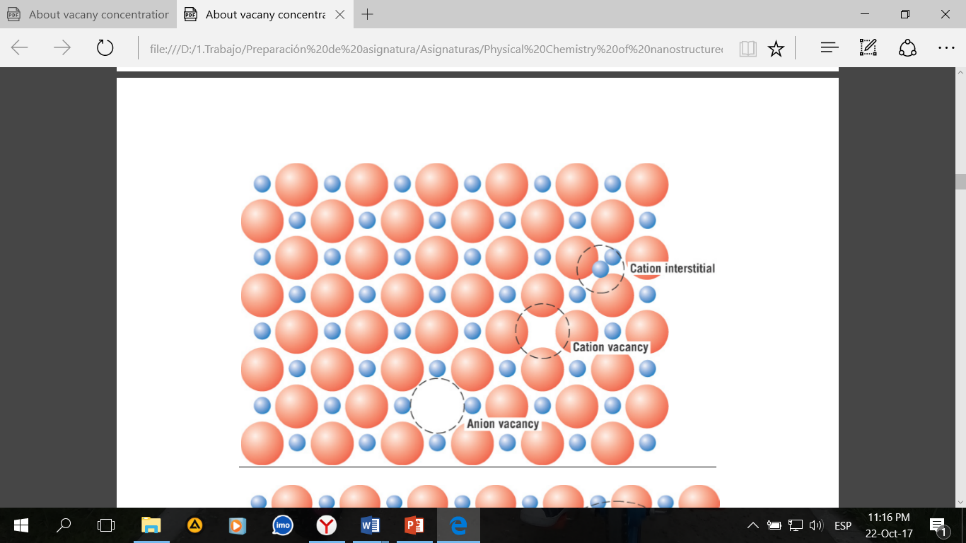
Let´s see what is the meaning of vacancy?

Perfect infinite lattice does not exist. Even, at thermodynamic equilibrium defects still exist. And material properties often depend on defects. In Fig. 1 you have an example of vacancy and a real photo for a vacancy. It is a tiny void.

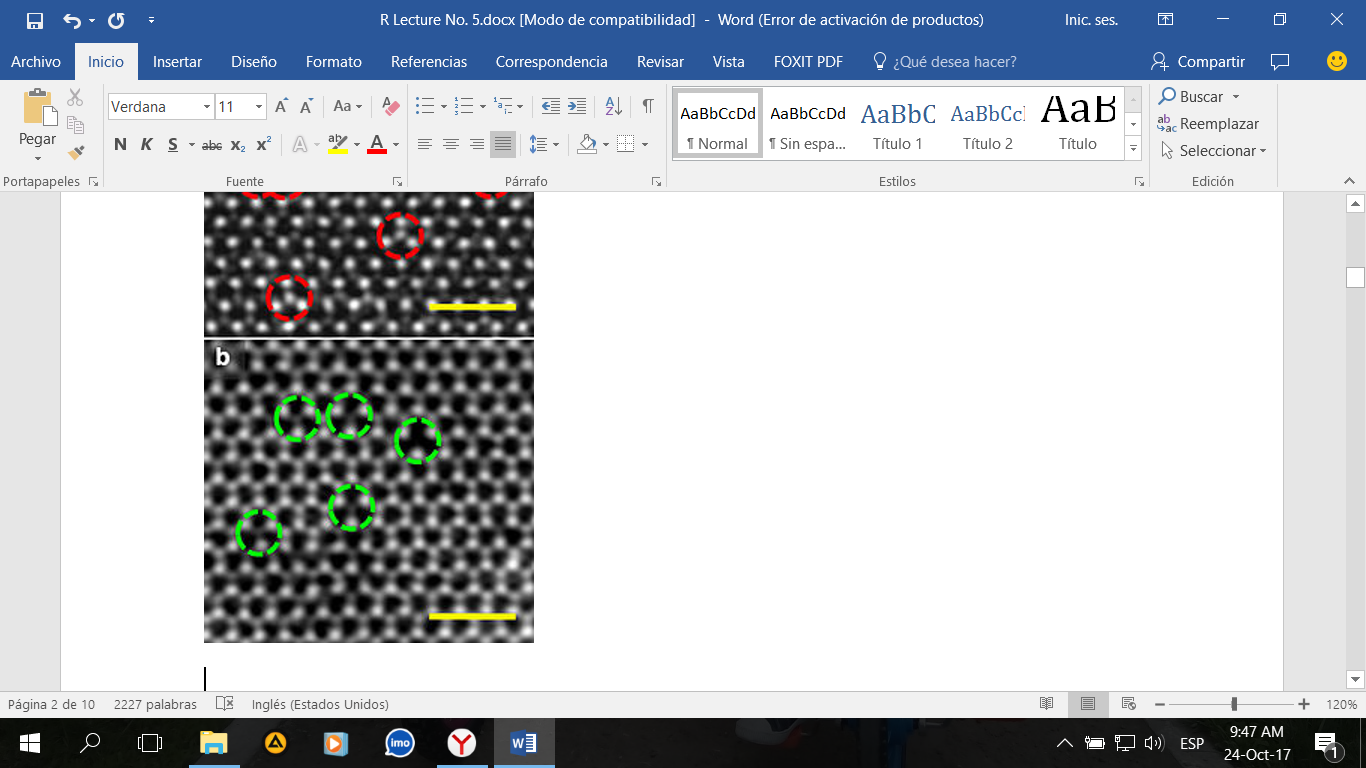(a) (b)

Fig. 1. Vacancy concentration of nanocrystals (a) and (b) vacancies in a monolayer of molybdenum disulfide. There is represented missed sulfur atoms.

Thus, as we said before these vacancies can change the properties of the solids.

The temperature of polymorphic transformation can decrease and lattice parameters increase the compressibility and solubility.

Let´s see the size effect influencing on the chemical equilibrium. According to the chemical thermodynamic of equilibrium, we can write the process of transformation of the reagent into a product as follow:

(1)

where μi and νi - corresponding stoichiometric coefficients. And A and B are reagent reactant and final product.

The equilibrium constant for fixed pressure and temperature associated with the standard change in the Gibbs energy equation:

(2)

Where:

K is the Boltzman constant,

T is the temperature,

K_p is the equilibrium constant.

In the standard state ΔG^O expressed by the equation:

(3)

At normal temperature and pressure.

Remember that free Gibbs energy can be calculated also by the following equation:

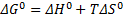
Where:

∆H⁰ is enthalpy,

∆S⁰ is entropy,

T is the temperature.

And we can use this expression only for massive phase.

Using fine particles can significantly change the equilibrium of the system. Theoretical studies of the thermodynamics of small particles and experiment show that the particle size is the active thermodynamic variable determining, together with other thermodynamic variables, the state of the system.

Size performs the role of temperature. This can be used for reactions where the equilibrium is shifted toward the starting materials. If the reaction is between nanoparticles, the equilibrium can be shifted towards the reaction products, because the value of the Gibbs potential particulate reagent is different from the default values of the bulk material. For reactions between substances in a state of change Nano dispersed Gibbs potential can be written as:

(4)

Where:

σ – surface-tension,

F - surface area,

V - volume of the dispersed particles,

ρ - density,

C_R - the relative number of vacancies per atom,

Ri - the radius of the particles,

C∞ - the concentration of vacancies in the array,

A - atomic weight,

N_A- Avogadro's number.

In equation (4), the first term represents the contribution of the surface energy, and the second - of vacancies. If the reaction product is dispersed, the Gibbs potential shift according to the equation (4). Then the change in the Gibbs potential for reaction (4) can be written as an equation:

(5)

where the summation is over Nano dispersed reagents. The reaction is possible if:

G_i › G_j, then ∆G ‹ 0

Substitution (4) into (5), then (5) to (2) give an expression for the equilibrium constant Kp as:

(9)

Where:

Kp∞ - bulk sample constant,

K_p – nanoparticle sample constant,

Ri the radius value represents the size effect.

Summarizing, there can be reactions between nanoparticles that are thermodynamically forbidden for massive materials, because the equilibrium constant for reactions between nanoparticles include, in contrast to the reaction with massive materials, many other factors like: radius, surface tensions, density, concentrations of vacancies, and so on.

Let´s see other properties of nanocrystals.