Кинетические уравнения реакций

Кинетическое уравнение необратимой реакции первого порядка

Рассмотрим необратимую (одностороннюю) реакцию распада:

A ® B + D.

Кинетическое уравнение:

.

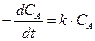Начальные условия: концентрация вещества А в начальный момент времени (t =0) равна C_A0.

Уравнения данного типа решаются методом разделения переменных:

® ® , ,

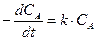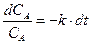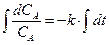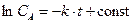при t =0; C = C_A0 , ,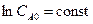

.

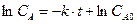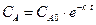Рис. 6‑4 Изменение концентрации вещества А во времени при протекании односторонней реакции первого порядка (C_A0=1)

Поскольку концентрация вещества А уменьшается в ходе реакции (рис.6.4) и асимптотически приближается к нулю, рассчитать точно время полного превращения вещества А невозможно. Для оценки времени протекания реакции используется такая характеристика, как время полупревращения (полураспада) – время, за которое прореагировала половина исходного вещества, т. е. концентрация вещества А уменьшилась в два раза ( 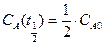): 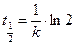. Время полупревращения для реакций первого порядка не зависит от исходной концентрации вещества, а определяется только величиной константы скорости.

Кинетическое уравнение необратимой реакции второго порядка.

К необратимым реакциям второго порядка относятся химические реакции типа:

A + A ® A₂, A + B ® AB, A + BС ® AB + С.

Рассмотрим как наиболее простую первую реакцию. Ее кинетическое уравнение имеет вид

.

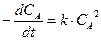Начальные условия: концентрация вещества А в начальный момент времени (t =0) равна c_A0:

, , , ,

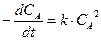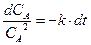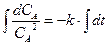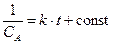при t =0; С = С_A0 , ,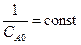

.

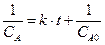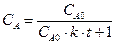Рис. 6‑5 Изменение концентрации вещества А во времени при протекании реакции второго порядка (C_A0=1)

Зависимость концентрации вещества от времени для реакций второго порядка (рис. 6.5) линейна в координатах 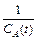– t, причем тангенс угла наклона равен константе скорости реакции.

Время полупревращения для реакций второго порядка зависит от исходной концентрации вещества А: .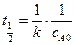

Реакции нулевого порядка.

Скорость реакций нулевого порядка не зависит от концентраций реагентов и определяется другими лимитирующими факторами, например площадью поверхности катализатора (в реакциях гетерогенного катализа) или поглощением света (в фотохимических реакциях):

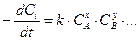, x+ y +…=0.

Кинетическое уравнение реакций нулевого порядка имеет вид

.

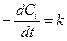Изменение концентрации реагирующих веществ во времени будет описываться уравнением

.

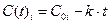Время полупревращения .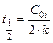

Кинетическое уравнение обратимой реакции первого порядка.

Изменение концентрации исходных веществ и продуктов реакции во времени в случае протекания обратимой (двусторонней) реакции можно показать на примере реакции первого порядка: А↔В.

Согласно закону действующих масс скорость прямой и обратной реакций будут описываться уравнениями

, .

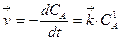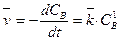Изменение концентраций исходного вещества А и продукта В определяется разностью скоростей прямого и обратного процессов:

, .

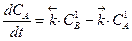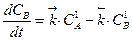Кинетические уравнения содержат три переменные: C_A,C_B и t. Для интегрирования одну необходимо исключить. Это можно сделать на основе материального баланса. Пусть в начальный момент времени при t=0 концентрация исходного вещества А равняется C_0A, а концентрация продукта В – C_0B, к моменту времени t согласно уравнению реакции концентрации реагентов изменятся на величину x: C_A = C_A0 – x, C_B= C_B0 + x.

Тогда , ,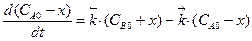

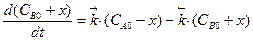и соответственно .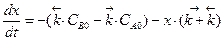

Учитывая, что при t=0 x=0, решением уравнения будет:

.

.

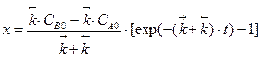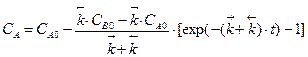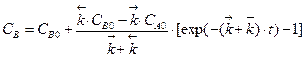Изменение концентрации веществ А и В во времени приведено на рис.6.6.

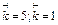Рис. 6‑6 Изменение концентрации веществ А и В во времени при протекании обратимой реакции первого порядка А↔В. ; C_0A=1; C_0B=0

Рис. 6‑7 Изменение во времени скоростей прямой и обратной реакций первого порядка А↔В: 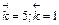; C_0A=1; C_0B=0

По достижении равенства скоростей прямой и обратной реакции (рис.6.7) концентрации исходного вещества и продукта изменяться не будут (в данном примере С_Ар=0,167; С_Вр=0,833), система придет в состояние равновесия.

Кинетические уравнения последовательных и параллельных реакций.

Принцип независимости протекания реакций заключается в том, что если в системе происходит несколько элементарных реакций, то каждая из них протекает по тем же законам, как и в отсутствии других реакций. Следовательно, если в нескольких реакциях участвует одно и то же вещество, то изменение его концентрации будет равно алгебраической сумме скоростей каждой реакции, умноженной на стехиометрический коэффициент этого вещества в данной реакции.

В случае последовательных реакций вещество, образующееся в первой реакции, является исходным для другой. Например, последовательная односторонняя реакция первого порядка:

Система кинетических уравнений для нее будут иметь вид:

, , .

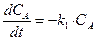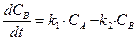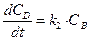Результаты численного решения уравнений приведены на рис.6.8.

Рис. 6‑8 Зависимость концентрации исходного (C_A) промежуточного (C_B) и конечного (C_D) веществ от времени для последовательной односторонней реакции первого порядка (k₁ = 0,5; k₂ = 0,3; C_0A=1).

В случае параллельных реакций одно вещество является исходным для нескольких реакции. Например, две реакции первого порядка:

Система кинетических уравнений в этом случае будет иметь вид:

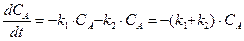
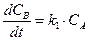
Аналогичным образом составляется система дифференциальных кинетических уравнений и для более сложных реакций. Например, параллельно-последовательные, с реакциями, как первого, так и второго порядков:

.

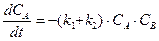
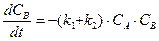
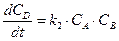
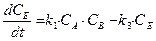
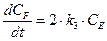Такие системы уравнений решают, как правило, численными методами.