Химическая связь в твердом теле

В твердом состоянии вещества образующие его частицы находятся в фиксированных положениях в пространстве, вокруг которых они совершают колебательные и вращательные движения. Различают кристаллические и аморфные твердые тела. В кристаллах существует пространственная периодичность в равновесных положениях частиц, а в аморфных твердых телах частицы колеблются около хаотически расположенных точек.

Основные понятия о строении кристаллов

Кристалл – тело, которое вследствие строго определенного внутреннего строения имеет самопроизвольно образующуюся форму, ограниченную плоскими гранями. Для кристаллов характерны правильные формы и симметрия. Атомы, образующие кристалл, располагаются строго определенным образом, соответствующим состоянию с минимумом энергии. Закономерности этого расположения определяются типом химических связей, существующих между атомами, и в известном смысле кристалл можно рассматривать как одну “большую молекулу”.

В зависимости от характера химической связи между частицами, образующими кристаллы, они подразделяются на четыре типа: молекулярные, ковалентные, ионные, металлические.

Для многих кристаллических веществ минимум энергии системы достигается при таком взаимном расположении частиц в пространстве, которое соответствует плотнейшей упаковке твердых шаров.

В плоскости твердые шары располагаются плотнейшим образом если каждый шар окружают шесть соседей. Второй слой шаров помещается во впадины, образованные тремя соприкасающимися шарами. При укладке третьего слоя появляются два возможных варианта, поскольку имеется два различных типа впадин: впадины, которые находятся над центрами шаров первого слоя, и впадины, которые располагаются над пустотами первого слоя (рис. 4.3). Поэтому существуют два возможных варианта плотнейшей упаковки:

1) гексагональная (ГПУ). Шары третьего слоя помещаются во впадины, которые находятся над центрами шаров первого слоя. Расположение слоев по вертикали повторяется в последовательности 1,2,1,2,... Повторение позиции шаров в нечетных и четных слоях;

2) кубическая (КПУ). Шары третьего слоя помещаются во впадины, которые располагаются над пустотами первого слоя. Расположение слоев по вертикали повторяется в последовательности 1,2,3,1,2,3,..

Рис. 4‑3 Первые два слоя плотнейшей упаковки шаров

При плотнейшей упаковке шаров в кристалле образуются пустоты двух типов: тетраэдрические, заключенные между четырьмя сферами, и октаэдрические – между шестью сферами. Пустоты играют важную роль в процессах диффузии и образования дефектов кристаллов. Если кристалл, например (Na⁺Cl^-), состоит из частиц разного размера, то частицы крупного размера ( 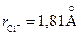) образуют плотнейшую упаковку, а частицы меньшего размера ( 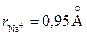) располагаются в пустотах.

Прямые линии, мысленно проведенные через центры частиц, создают так называемую кристаллическую решетку. Точки пересечения этих линий называются узлами кристаллической решетки, в которых располагаются образующие ее частицы. Кристаллическую решетку можно охарактеризовать элементарной ячейкой, которая представляет собой минимальный фрагмент решетки, полностью отражающий геометрию решетки и чередование частиц в кристалле (рис. 4.4).

Рис. 4‑4 Кристаллическая решетка и ее элементарная ячейка

Элементарная ячейка является структурной единицей кристалла, ее параллельным переносом можно построить кристаллическую решетку. В трехмерном пространстве элементарная ячейка представляет собой варианты параллелепипеда с различным соотношением ребер и углов между ними.

Размеры элементарной ячейки называются постоянными решетки. В зависимости от равенства или неравенства этих углов между собой различают семь классов (сингоний) и 14 типов элементарных ячеек, которым соответствуют кристаллические решетки. Самая несимметричная решетка – триклинная ( 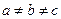, 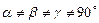), а самая симметричная – кубическая, для которой возможны три варианта элементарной ячейки: простейшая кубическая решетка – ПК, кубическая объемоцентрированная решетка – ОЦК и кубическая гранецентрированная решетка – ГЦК (рис. 4.5).

Рис. 4‑5 Типы элементарных ячеек кубических кристаллических решеток

Число ближайших соседних частиц, находящихся на одинаковом расстоянии, от атома или иона, расположенного в узле решетки, называется координационным числом (КЧ).

В зависимости от внешних условий (давление, температура) одно и то же вещество может существовать в состояниях с различными типами кристаллических решеток. Это явление называется полиморфизмом, а переход вещества из одного кристаллического состояния (полиморфной модификации) в другое – полиморфным переходом.

Вследствие упорядоченного фиксированного положения частиц в кристаллах они обладают анизотропией физических и химических свойств - зависимостью этих свойств от выбранного направления в кристалле. Поэтому важной характеристикой кристаллического тела является его кристаллографическая ориентация, то есть соответствие плоскостей поверхности тела кристаллографическим плоскостям. Плоскости, мысленно проведенные через узлы решетки, называются кристаллографическими. Ряд параллельных кристаллографических плоскостей обозначают индексами Миллера, которые определяют следующим образом. Находят пересечение плоскости с осями координат, соответствующих элементарной ячейке (оси координат направлены вдоль ребер, углы между ними равны a, b, g). Отрезки, отсекаемые плоскостью на осях, измеряют в длинах ребер элементарной ячейки (x, y, z). Затем обратные значения этих величин умножают на соответствующие числа так, чтобы получить три наименьших возможных целых числа, которые и называются индексами Миллера (h, k, l): .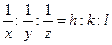

Вследствие симметрии кристаллической решетки отдельные плоскости образуют группы эквивалентных плоскостей. Например, равнозначными в кубических кристаллах являются плоскости (100), (010), (001), …. Группа эквивалентных плоскостей обозначается {100}.

Направления в кристалле определяется индексами Миллера [h, k, l] плоскости перпендикулярной к заданному направлению.

Пример. В кубических кристаллах основными кристаллографическими плоскостями являются (1,0,0) – грань куба, (1,1,0) диагональная плоскость куба, проходящая через два ребра, (1,1,1) – диагональная плоскость, проходящая через три вершины (рис. 4.6).

Рис. 4‑6 Индексы Миллера для обозначения основных кристаллографических плоскостей в кубическом кристалле