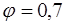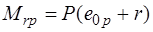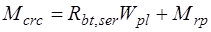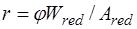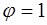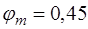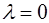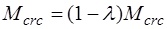РАСЧЕТ ПО ОБРАЗОВАНИЮ ТРЕЩИН В ИЗГИБАЕМЫХ И ВНЕЦЕНТРЕННО ЗАГРУЖЕННЫХ ЭЛЕМЕНТАХ
Изгибаемые, внецентренно сжатые и внецентренно растянутые элементы рассчитываются на трещиностойкость по способу «ядровых» моментов, то есть моментов относительно оси, проходящей через точку, лежащую на границе ядра сечения наиболее удаленную от растянутой зоны, которая и называется ядровой точкой. Этот расчет заключается в проверке условия
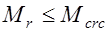 , (25.1) где
, (25.1) где 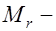 момент от внешних нагрузок в рассматриваемом сечении относительно оси, параллельной нейтральной оси сечения и проходящей через ядровую точку (рис. 25.1);
момент от внешних нагрузок в рассматриваемом сечении относительно оси, параллельной нейтральной оси сечения и проходящей через ядровую точку (рис. 25.1); 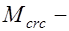 момент относительно той же оси, воспринимаемый сечением при образовании трещин.
момент относительно той же оси, воспринимаемый сечением при образовании трещин.
Положение ядровой точки определяется ее расстоянием 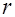 от центра тяжести приведенного сечения. Величину
от центра тяжести приведенного сечения. Величину 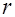 с целью учета неупругих деформаций бетона сжатой зоны принимают в зависимости от вида силового воздействия (рис. 25.1, 25.2, 25.3). Для внецентренно сжатых и изгибаемых элементов имеем
с целью учета неупругих деформаций бетона сжатой зоны принимают в зависимости от вида силового воздействия (рис. 25.1, 25.2, 25.3). Для внецентренно сжатых и изгибаемых элементов имеем
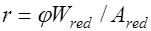 , (25.2) где
, (25.2) где 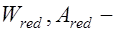 момент упругого сопротивления и площадь приведенного сечения,
момент упругого сопротивления и площадь приведенного сечения,
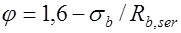 ;
; 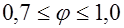 . (25.3)
. (25.3)
Для элементов без предварительного напряжения 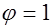 . Этот коэффициент учитывает неупругую работу сжатой зоны бетона,
. Этот коэффициент учитывает неупругую работу сжатой зоны бетона, 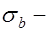 максимальные напряжения в сжатом бетоне от внешней нагрузки и усилия предварительного обжатия
максимальные напряжения в сжатом бетоне от внешней нагрузки и усилия предварительного обжатия 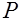 , определяемые с учетом упругой работы приведенного сечения
, определяемые с учетом упругой работы приведенного сечения
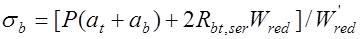 , (25.4) где
, (25.4) где 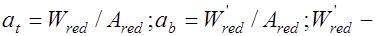 момент сопротивления крайних сжатых волокон.
момент сопротивления крайних сжатых волокон.
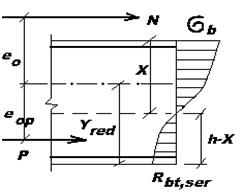
Если положение нейтральной оси приведенного сечения 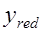 определить относительно крайних растянутых волокон бетона (рис. 25.1), то
определить относительно крайних растянутых волокон бетона (рис. 25.1), то 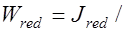
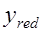 ,
, 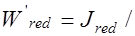
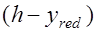 .
.
Выражение (25.4) получается из рассмотрения деформированного состояния сечения. Например, для элементов без предварительного напряжения согласно эпюре деформаций сечения (рис. 25.4) краевые деформации бетона сжатой зоны равны:
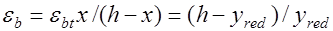 . (25.5)
. (25.5)
При упругой работе 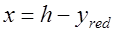 . Тогда для напряжений
. Тогда для напряжений 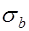 имеем
имеем
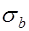
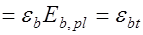
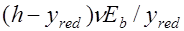 . (25.6)
. (25.6)
Очевидно, что перед образованием трещин деформации в растянутом бетоне составят
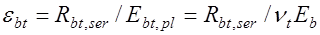 .
.
В этом случае 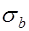
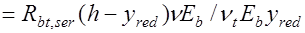 .
.
При учете лишь упругих деформаций имеем 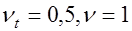 , тогда
, тогда
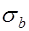
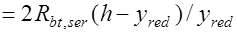
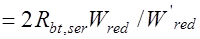 . (25.7)
. (25.7)
Для внецентренно растянутых элементов при 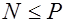 ядровое расстояние определяется по формуле (25.2), если же
ядровое расстояние определяется по формуле (25.2), если же 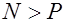 , то
, то
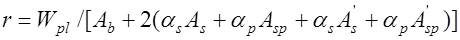 , (25.8) где
, (25.8) где 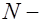 внешнее усилие;
внешнее усилие; 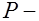 усилие предварительного обжатия;
усилие предварительного обжатия; 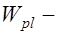 момент сопротивления приведенного сечения для крайних растянутых волокон с учетом неупругих деформаций бетона, определяемый в предположении отсутствия
момент сопротивления приведенного сечения для крайних растянутых волокон с учетом неупругих деформаций бетона, определяемый в предположении отсутствия 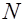 и
и 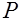 :
:
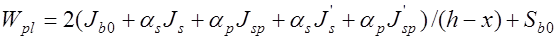 ;
;
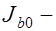 момент инерции сжатой площади бетона относительно нейтральной оси;
момент инерции сжатой площади бетона относительно нейтральной оси; 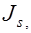
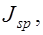
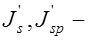 моменты инерции площадей растянутой и сжатой арматуры относительно нейтральной оси;
моменты инерции площадей растянутой и сжатой арматуры относительно нейтральной оси; 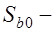 статический момент растянутой зоны бетона относительно нейтральной оси. Положение нейтральной оси можно определить из условия:
статический момент растянутой зоны бетона относительно нейтральной оси. Положение нейтральной оси можно определить из условия:
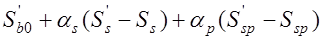 ,
,
где 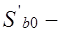 статический момент сжатой зоны бетона;
статический момент сжатой зоны бетона; 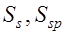 и
и 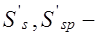 статические моменты растянутой и сжатой арматуры относительно нейтральной оси.
статические моменты растянутой и сжатой арматуры относительно нейтральной оси.
Момент сопротивления 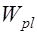 допускается определять по упрощенной формуле:
допускается определять по упрощенной формуле:
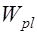
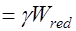 , где
, где 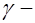 коэффициент, учитывающий неупругие деформации растянутого бетона, он принимается в зависимости от формы сечения (для прямоугольного и таврового сечений с полкой в сжатой зоне
коэффициент, учитывающий неупругие деформации растянутого бетона, он принимается в зависимости от формы сечения (для прямоугольного и таврового сечений с полкой в сжатой зоне 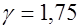 ).
).
Если определено ядровое расстояние, то можно непосредственно выполнить расчет согласно условию (25.1). При этом момент, воспринимаемый нормальным сечением перед образованием трещин, вычисляется следующим образом
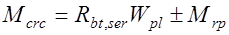 , (25.9)
, (25.9)
где 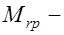 ядровый момент обжатия от усилия
ядровый момент обжатия от усилия 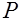 , определяемый относительно оси, проходящей через ядровую точку (знак плюс принимается когда направление моментов
, определяемый относительно оси, проходящей через ядровую точку (знак плюс принимается когда направление моментов 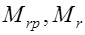 противоположны);
противоположны); 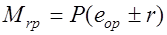 ;
; 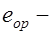 эксцентриситет приложения усилия
эксцентриситет приложения усилия 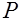 , здесь знак плюс соответствует усилию
, здесь знак плюс соответствует усилию 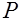 сжимающему растянутую зону.
сжимающему растянутую зону.
Очевидно, что для изгибаемых элементов 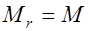 , для внецентренного сжатых
, для внецентренного сжатых 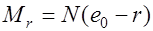 , для внецентренно растянутых
, для внецентренно растянутых 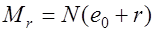 (рис. 25.2, 25.3).
(рис. 25.2, 25.3).
Приведенная методика расчета элементов, работающих по двухзначной эпюре напряжений относится к случаю когда в сжатой зоне нет начальных трещин, вызванных воздействием на эту зону растягивающих напряжений от усилия предварительного обжатия. Трещин от усилия обжатия, как правило, допускать не следует. Однако если же они образовались, то трещиностойкость растянутой зоны от внешних нагрузок будет снижена. В этом случае 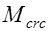 для растянутой зоны следует снижать на величину
для растянутой зоны следует снижать на величину 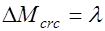
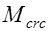 , где
, где 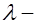 коэффициент, определяемый по формуле
коэффициент, определяемый по формуле 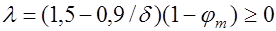 ,
,
где 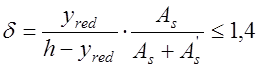 ;
; 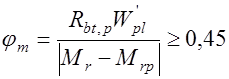 ;
;
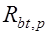 соответствует при этом передаточной прочности бетона
соответствует при этом передаточной прочности бетона 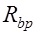 .
.
25.2. АЛГОРИТМ РАСЧЕТА ПО ТРЕЩИНОСТОЙКОСТИ НОРМАЛЬНЫХ СЕЧЕНИЙ
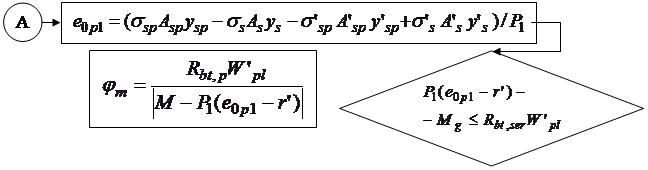
Алгоритм автоматизированного расчета трещиностойкости сечений центрально растянутых элементов может быть представлен блок-схемой 25.1. Построение алгоритма автоматизированного расчета сечений элементов, работающих с двухзначной эпюрой напряжений рассмотрим на примере изгибаемых элементов двутаврового профиля. Алгоритм представим в виде блок-
схемы 25.2, где 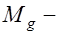 момент от собственного веса элемента.
момент от собственного веса элемента.
Блок-схема 25.1
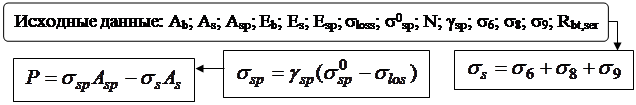 |

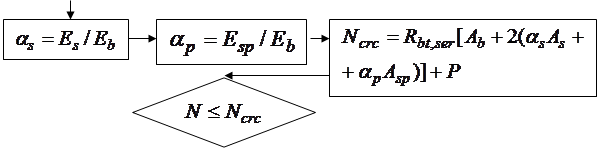 |

ДА
Трещиностойкость обеспечена
 | |||
 | |||
НЕТ
Блок-схема 25.2
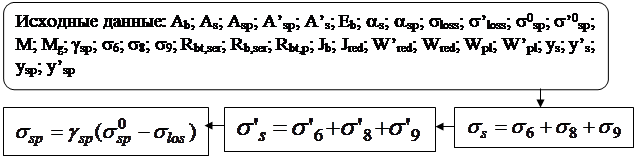 |
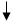
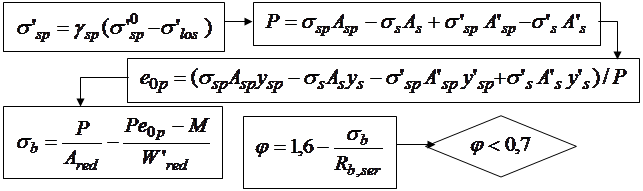
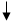

 НЕТ
НЕТ
|

 ДА
ДА


|

|
|
|


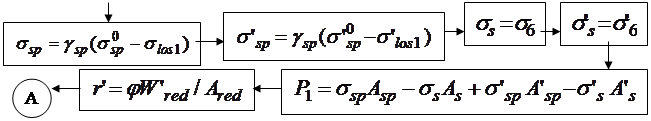 | ||
 |
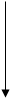

 НЕТ
НЕТ


|

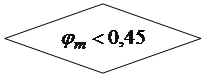 ДА
ДА
 | |||
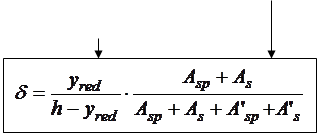 | |||
|
 | |||||
 | |||||
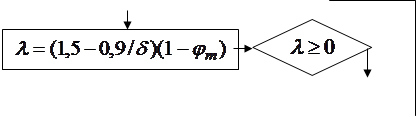 | |||||
|

|
 | |||
 |
 |
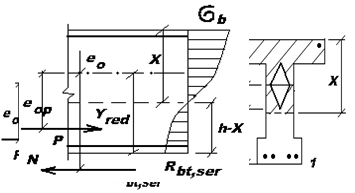 |
Рис. 25.1 Рис. 25.2
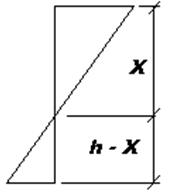 |
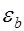

Рис. 25.3 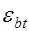
Рис. 25.4
| <== предыдущая лекция | | | следующая лекция ==> |
| РАСЧЕТ ПРОЧНОСТИ ВНЕЦЕНТРЕННО РАСТЯНУТЫХ ЭЛЕМЕНТОВ | | | РАСЧЕТ ПО РАСКРЫТИЮ НОРМАЛЬНЫХ ТРЕЩИН В ЦЕНТРАЛЬНО РАСТЯНУТЫХ, ИЗГИБАЕМЫХ И ВНЕЦЕНТРЕННО ЗАГРУЖЕННЫХ ЭЛЕМЕНТАХ |
Дата добавления: 2018-09-24; просмотров: 1873;