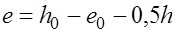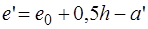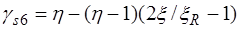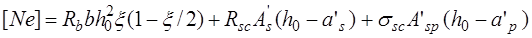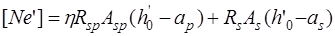РАСЧЕТ ПРОЧНОСТИ ВНЕЦЕНТРЕННО РАСТЯНУТЫХ ЭЛЕМЕНТОВ
Предельное состояние по несущей способности элемента любого симметричного сечения, внецентренно растянутых в плоскости симметрии и работающих по первой схеме, то есть при  характеризуется тем, что бетон в элементах пересечен сквозными трещинами вследствие того, что все сечение растянуто. Поэтому внешнему усилию сопротивляется лишь продольная арматура. Элемент разрушается когда напряжения во всей арматуре достигнут предельных значений. Несущая способность в этом случае проверяется по условиям (рис. 24.1):
характеризуется тем, что бетон в элементах пересечен сквозными трещинами вследствие того, что все сечение растянуто. Поэтому внешнему усилию сопротивляется лишь продольная арматура. Элемент разрушается когда напряжения во всей арматуре достигнут предельных значений. Несущая способность в этом случае проверяется по условиям (рис. 24.1):
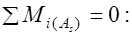
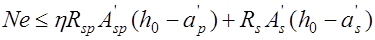 ; (24.1)
; (24.1)
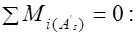
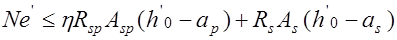 ; (24.2)
; (24.2)
где  ;
; 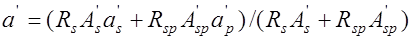 .
.
В элементах работающих по схеме 2, то есть при 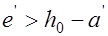 , предельное состояние по несущей способности сечений подобно изгибаемых конструкций. Здесь часть сечения, удаленная от линии действия силы
, предельное состояние по несущей способности сечений подобно изгибаемых конструкций. Здесь часть сечения, удаленная от линии действия силы 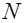 , сжата, противоположная часть – растянута. Очевидно, что при наличии трещин в бетоне растянутой зоны соответствующие усилия воспринимаются арматурой. Несущая способность элемента определяется сопротивлением растяжению арматуры и предельным сопротивлением сжатой зоны бетона и ненапрягаемой арматуры, установленной в сжатой зоне. При наличии предварительно напряженной арматуры в сжатой зоне напряжения в ней
, сжата, противоположная часть – растянута. Очевидно, что при наличии трещин в бетоне растянутой зоны соответствующие усилия воспринимаются арматурой. Несущая способность элемента определяется сопротивлением растяжению арматуры и предельным сопротивлением сжатой зоны бетона и ненапрягаемой арматуры, установленной в сжатой зоне. При наличии предварительно напряженной арматуры в сжатой зоне напряжения в ней 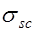 не достигают предельного сопротивления и определяются также как для изгибаемых элементов
не достигают предельного сопротивления и определяются также как для изгибаемых элементов
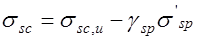 , (24.3) где
, (24.3) где 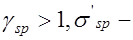 принимаются с учетом всех потерь.
принимаются с учетом всех потерь.
Несущая способность прямоугольных сечений в этом случае определяется по формуле (рис. 24.2)
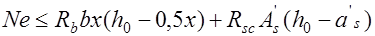
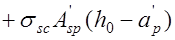 , (24.4)
, (24.4)
или 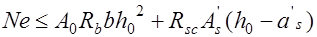
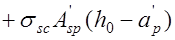 .
.
Высота сжатой зоны вычисляется из уравнения
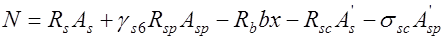 , (24.5) или
, (24.5) или 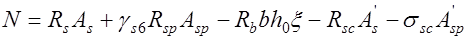 ,
,
где 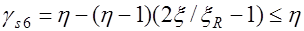 .
.
Условие (24.4) справедливо при 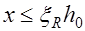 , если же из уравнения (24.5) получим, что
, если же из уравнения (24.5) получим, что 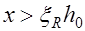 , то в условии (24.4)
, то в условии (24.4) 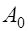 следует заменить на
следует заменить на 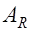 . Если же из уравнения (24.5) получим, что
. Если же из уравнения (24.5) получим, что 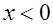 , то прочность следует определять из условия (24.2). Если при
, то прочность следует определять из условия (24.2). Если при 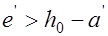 высота сжатой зоны, определенная без учета ненапрягаемой арматуры площадью
высота сжатой зоны, определенная без учета ненапрягаемой арматуры площадью 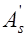 составит
составит 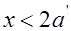 , то при определении несущей способности следует использовать условие (24.4) без учета арматуры
, то при определении несущей способности следует использовать условие (24.4) без учета арматуры 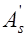 .
.
При расчете внецентренно растянутых элементов встречаются в основном два типа задач:
а) известны 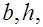
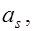
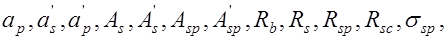
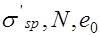 . Требуется проверить прочность сечения;
. Требуется проверить прочность сечения;
б) известны 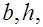
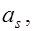
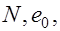
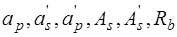 ,
, 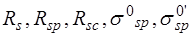 .
.
Требуется определить 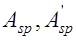 .
.
Задачи второго типа могут иметь несколько интерпретаций в зависимости от того, что известно из величин 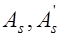 ,
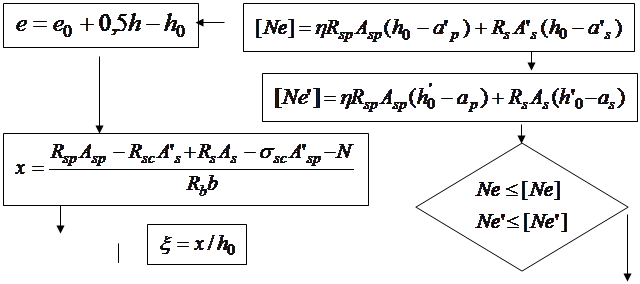
, 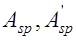 . Для примера проиллюстрируем алгоритм решения задач первого типа, который представлен в блок-схеме 24.1. При решении задач второго типа алгоритм строится по аналогии с изгибаемыми элементами и с учетом блок-схемы 24.1.
. Для примера проиллюстрируем алгоритм решения задач первого типа, который представлен в блок-схеме 24.1. При решении задач второго типа алгоритм строится по аналогии с изгибаемыми элементами и с учетом блок-схемы 24.1.
24.2. РАСЧЕТ ПО ОБРАЗОВАНИЮ ТРЕЩИН В РАСТЯНУТЫХ ЭЛЕМЕНТАХ
Практика показывает, что расчет элементов по первой группе предельных состояний в ряде случает может оказаться не достаточным для обеспечения нормальной эксплуатации конструкций, если их прогибы или ширина раскрытия трещин будут недопустимо велики, либо образуются трещины, которых быть не должно. Поэтому требуется провести соответствующий расчет во избежание проявления негативных последствий.
За основу расчета по образованию трещин принимают напряженно-деформированное состояние элемента в стадии работы без трещин. Считается, что появление трещин в растянутом бетоне происходит тогда, когда удлинения элемента достигают предельных значений, а напряжения растяжения –  . В этот момент напряжения в напрягаемой арматуре будут равны сумме предварительного напряжения с учетом всех потерь и приращения напряжений за счет деформаций растянутого бетона после погашения его обжатия
. В этот момент напряжения в напрягаемой арматуре будут равны сумме предварительного напряжения с учетом всех потерь и приращения напряжений за счет деформаций растянутого бетона после погашения его обжатия 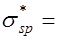
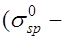
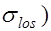
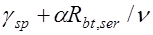 ;
; 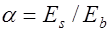 , где
, где 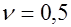 (рис. 24.3).
(рис. 24.3).
Напряжения в ненапрягаемой арматуре предварительно напряженных конструкций равно сумме сжимающего напряжения от усадки, ползучести бетона и приращения растягивающих напряжений за счет деформаций растянутого бетона
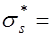
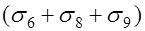
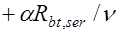 .
.

 В центрально растянутых элементах трещины образовываться не будут, если усилие от внешних нагрузок
В центрально растянутых элементах трещины образовываться не будут, если усилие от внешних нагрузок 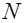 не превысит усилия, воспринимаемого сечением при образовании трещин
не превысит усилия, воспринимаемого сечением при образовании трещин 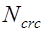 , то есть
, то есть 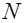
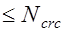 . Усилие
. Усилие 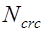 определяют по напряжениям, возникающим в сечениях арматуры и бетона. В общем случае имеем (рис. 24.3)
определяют по напряжениям, возникающим в сечениях арматуры и бетона. В общем случае имеем (рис. 24.3)
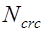
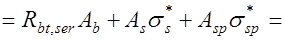
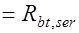
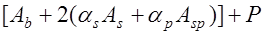 , (24.6) где
, (24.6) где 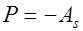
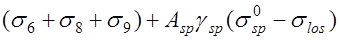 ;
; 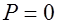 при
при 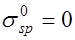 .
.
Блок-схема 24.1
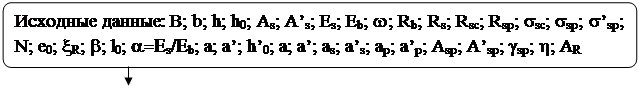 |
|
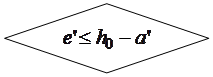


|
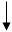

 НЕТ
НЕТ
 | |||
 |

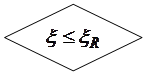

 ДА НЕТ
ДА НЕТ
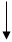 ДА
ДА 
A:Прочность обеспечена


|



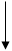
 НЕТ
НЕТ

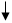

|


 ДА НЕТ
ДА НЕТ



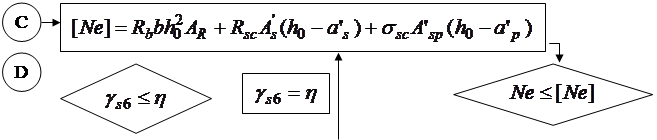
НЕТ


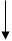
НЕТ ДА




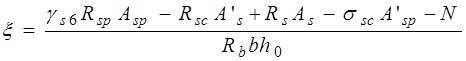
 ДА
ДА
НЕТ
 |
|
 | ||||
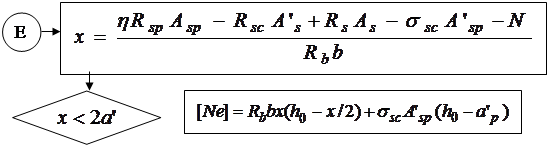 | ||||
 | ||||

 ДА
ДА
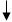 |

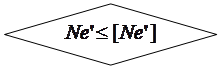
|
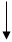


|

|
 НЕТ
НЕТ
 |  |
 | 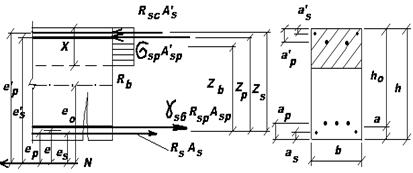 |
Рис. 24.1 Рис. 24.2
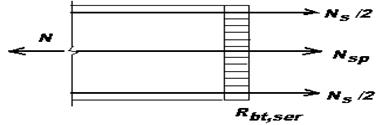 |
Рис. 24.3
| <== предыдущая лекция | | | следующая лекция ==> |
| РАСЧЕТ ВНЕЦЕНТРЕННО СЖАТЫХ ЭЛЕМЕНТОВ КОЛЬЦЕВОГО СЕЧЕНИЯ | | | РАСЧЕТ ПО ОБРАЗОВАНИЮ ТРЕЩИН В ИЗГИБАЕМЫХ И ВНЕЦЕНТРЕННО ЗАГРУЖЕННЫХ ЭЛЕМЕНТАХ |
Дата добавления: 2018-09-24; просмотров: 1539;