РАСЧЕТ ПО РАСКРЫТИЮ НОРМАЛЬНЫХ ТРЕЩИН В ЦЕНТРАЛЬНО РАСТЯНУТЫХ, ИЗГИБАЕМЫХ И ВНЕЦЕНТРЕННО ЗАГРУЖЕННЫХ ЭЛЕМЕНТАХ
После образования трещин в растянутых элементах или растянутых зонах изгибаемых, внецентренно сжатых и внецентренно растянутых элементов при увеличении нагрузки происходит их раскрытие. На раскрытие трещин рассчитываются конструкции, к которым предъявляются требования второй и третьей категории трещиностойкости. Расчет производится по стадии работы элементов с трещинами в первом случае при 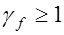 , а во втором – при
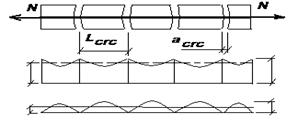
, а во втором – при 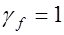 . Ширина раскрытия трещин, нормальных к продольной оси элемента, на уровне растянутой арматуры представляет собой разность удлинений арматуры и растянутого бетона на участке между трещинами длиной
. Ширина раскрытия трещин, нормальных к продольной оси элемента, на уровне растянутой арматуры представляет собой разность удлинений арматуры и растянутого бетона на участке между трещинами длиной 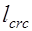 , то есть
, то есть
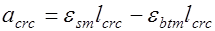 , (26.1) где
, (26.1) где 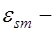 средние деформации растянутой арматуры;
средние деформации растянутой арматуры; 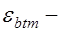 средние деформации растянутого бетона.
средние деформации растянутого бетона.
Пренебрегая величиной 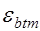 как малой по сравнению с
как малой по сравнению с 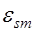 получим
получим
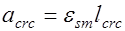 . (26.2)
. (26.2)
Средние деформации арматуры можно определить через максимальные следующим образом 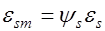 , где
, где 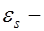 деформации растянутой арматуры в сечении с трещиной (рис. 26.1);
деформации растянутой арматуры в сечении с трещиной (рис. 26.1); 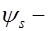 коэффициент, учитывающий работу бетона на участках между трещинами (
коэффициент, учитывающий работу бетона на участках между трещинами ( 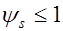 ).
).
Тогда вместо (26.2), учитывая, что 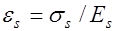 имеем
имеем
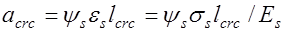 , (26.3) где
, (26.3) где 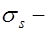 напряжения в растянутой арматуре в сечении с трещиной.
напряжения в растянутой арматуре в сечении с трещиной.
Расстояние между трещинами определяют из условия, что разность усилий в растянутой арматуре в сечениях с трещинами и между трещинами уравновешивается усилиями сцепления арматуры с бетоном. Так для центрально растянутых элементов
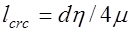 , (26.4) где
, (26.4) где 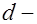 диаметр стержней;
диаметр стержней; 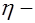 коэффициент, зависящий от вида и профиля арматуры;
коэффициент, зависящий от вида и профиля арматуры; 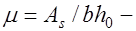 коэффициент армирования сечения или ребра таврового сечения.
коэффициент армирования сечения или ребра таврового сечения.
Тогда для растянутых элементов получим
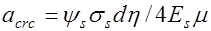 . (26.5)
. (26.5)
Эксперименты показали, что вследствие неоднородности бетона расстояния между трещинами могут отличаться от расчетных в большую или меньшую сторону в 1,5-1,8 раза.
Поэтому СНиП2.03.01-84 * рекомендует определять максимальную ширину раскрытия трещин, нормальных к продольной оси элемента по эмпирической зависимости (26.5) как для центрально растянутых элементов, так и для элементов, работающих по двузначной эпюре напряжений:
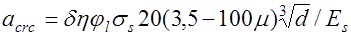 , (26.6) где
, (26.6) где 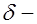 коэффициент, принимаемый для элементов изгибаемых и внецентренно сжатых равным
коэффициент, принимаемый для элементов изгибаемых и внецентренно сжатых равным 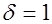 , для растянутых –
, для растянутых – 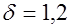 ;
; 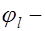 коэффициент, учитывающий длительность действия нагрузки, так при учете кратковременного действия нагрузки
коэффициент, учитывающий длительность действия нагрузки, так при учете кратковременного действия нагрузки 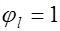 , при многократно повторяющейся нагрузке, для элементов при естественной влажности
, при многократно повторяющейся нагрузке, для элементов при естественной влажности 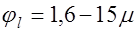 , а водонасыщенном состоянии
, а водонасыщенном состоянии 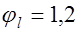 ;
; 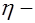 коэффициент, принимаемый для стержневой арматуры периодического профиля
коэффициент, принимаемый для стержневой арматуры периодического профиля 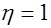 , для гладкой стержневой
, для гладкой стержневой 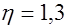 , проволочной периодического профиля
, проволочной периодического профиля 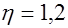 и гладкой проволочной
и гладкой проволочной 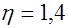 ;
; 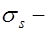 напряжения в растянутой продольной арматуре или приращение напряжений после погашения обжатия: для центрально растянутых элементов без преднапряжения
напряжения в растянутой продольной арматуре или приращение напряжений после погашения обжатия: для центрально растянутых элементов без преднапряжения 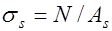 и с преднапряжением
и с преднапряжением 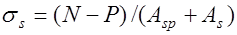 , для изгибаемых без преднапряжения
, для изгибаемых без преднапряжения 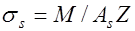 и для элементов с преднапряжением –
и для элементов с преднапряжением – 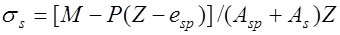 , для внецентренно растянутых при
, для внецентренно растянутых при 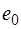
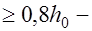
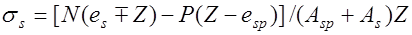 ,
, 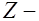 плечо внутренней пары сил, для внецентренно растянутых элементов при
плечо внутренней пары сил, для внецентренно растянутых элементов при 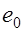
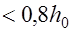 величина
величина 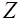 принимается равным расстоянию между центрами тяжести сжатой и растянутой арматуры;
принимается равным расстоянию между центрами тяжести сжатой и растянутой арматуры; 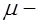 коэффициент армирования принимаемый не более 0,02; d – диаметр стержней, принимаемый в миллиметрах.
коэффициент армирования принимаемый не более 0,02; d – диаметр стержней, принимаемый в миллиметрах.
Формула (26.6) позволяет получить результаты достаточно близкие к экспериментальным. Для элементов второй категории трещиностойкости, ширина кратковременного раскрытия трещин определяется от суммарного воздействия постоянных, длительных и кратковременных нагрузок при 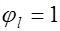 . Для элементов третьей категории трещиностойкости, ширина продолжительного раскрытия трещин определяется от действия постоянных и длительных нагрузок, а ширина кратковременного – определяется по нелинейной зависимости как сумма приращения ширина раскрытия трещин
. Для элементов третьей категории трещиностойкости, ширина продолжительного раскрытия трещин определяется от действия постоянных и длительных нагрузок, а ширина кратковременного – определяется по нелинейной зависимости как сумма приращения ширина раскрытия трещин 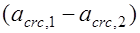 от кратковременного действия всех нагрузок при
от кратковременного действия всех нагрузок при 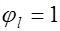 и ширины продолжительного раскрытия
и ширины продолжительного раскрытия 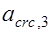 от постоянной и длительной нагрузок
от постоянной и длительной нагрузок
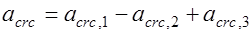 , (26.7)
, (26.7)
где 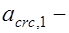 ширина раскрытия трещин от кратковременного действия всех нагрузок;
ширина раскрытия трещин от кратковременного действия всех нагрузок; 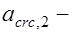 то же, но от кратковременного действия постоянной и длительной нагрузок;
то же, но от кратковременного действия постоянной и длительной нагрузок; 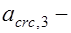 ширина раскрытия трещин от длительного действия постоянной и длительных нагрузок.
ширина раскрытия трещин от длительного действия постоянной и длительных нагрузок.
26.2. РАСЧЕТ ПО ДЕФОРМАЦИЯМ ЭЛЕМЕНТОВ, РАБОТАЮЩИХ БЕЗ ТРЕЩИН. ОПРЕДЕЛЕНИЕ КРИВИЗНЫ
Расчет перемещений железобетонных элементов – прогибов и углов поворота связан с определением кривизны оси при изгибе и внецентренных нагружениях. По длине железобетонного элемента в зависимости от вида нагружения и характера напряженного состояния могут быть участки без трещин и участки с трещинами в растянутой зоне. Встречаются также конструкции, работающие без трещин на всех участках. Это конструкции в основном первой категории трещиностойкости. Считается, что элементы или участки элементов, не имеют трещин в растянутой зоне, если при действии расчетных постоянных, длительных и кратковременных нагрузок с коэффициентом надежности по нагрузке 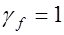 трещины не образуются по расчету. Кривизна изгибаемого или внецентренно загруженного продольной силой элемента на участках без трещин определяется как для сплошного приведенного сечения. При этом учитывается увеличение деформаций за счет ползучести бетона
трещины не образуются по расчету. Кривизна изгибаемого или внецентренно загруженного продольной силой элемента на участках без трещин определяется как для сплошного приведенного сечения. При этом учитывается увеличение деформаций за счет ползучести бетона
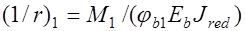 ;
; 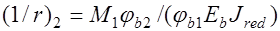 , (26.8) где
, (26.8) где 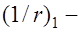 кривизна элемента от кратковременных нагрузок;
кривизна элемента от кратковременных нагрузок; 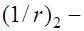 то же, но от постоянных и длительных нагрузок;
то же, но от постоянных и длительных нагрузок; 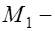 изгибающий момент от кратковременных внешних нагрузок относительно оси нормальной к плоскости действия изгибающего момента и проходящей через центр тяжести приведенного сечения;
изгибающий момент от кратковременных внешних нагрузок относительно оси нормальной к плоскости действия изгибающего момента и проходящей через центр тяжести приведенного сечения; 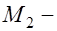 то же, но от постоянных и длительных нагрузок;
то же, но от постоянных и длительных нагрузок; 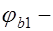 коэффициент, учитывающий влияние быстронатекающей ползучести бетона, принимаемый для тяжелого бетона
коэффициент, учитывающий влияние быстронатекающей ползучести бетона, принимаемый для тяжелого бетона 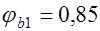 и
и 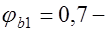 для легкого и поризованного бетона;
для легкого и поризованного бетона; 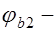 коэффициент, учитывающий влияние длительной ползучести бетона, принимаемый при постоянных и длительных нагрузках в зависимости от влажности воздуха и вида бетона
коэффициент, учитывающий влияние длительной ползучести бетона, принимаемый при постоянных и длительных нагрузках в зависимости от влажности воздуха и вида бетона 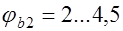 , так для тяжелого бетона при влажности окружающего воздуха 40 … 75 % –
, так для тяжелого бетона при влажности окружающего воздуха 40 … 75 % – 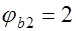 .
.
К конструкциям, работающим без трещин, обычно относятся предварительно напряженные. В этом случае расчетная кривизна элемента складывается из кривизны от усилий, создаваемых предварительным напряжением арматуры и от эксплуатационных нагрузок. Рассмотрим свободно опертую балку постоянного сечения. После освобождения продольной арматуры с упоров балка получает обжатие и выгиб 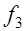 соответствующий кривизне
соответствующий кривизне 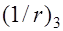 (рис. 26.2) от кратковременного действия усилия предварительного обжатия
(рис. 26.2) от кратковременного действия усилия предварительного обжатия 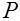 , определяемого с учетом всех потерь к рассматриваемому моменту времени. Тогда согласно (26.8) получим
, определяемого с учетом всех потерь к рассматриваемому моменту времени. Тогда согласно (26.8) получим
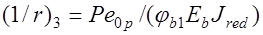 , (26.9) где
, (26.9) где 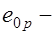 эксцентриситет усилия предварительного обжатия
эксцентриситет усилия предварительного обжатия 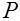 относительно центра тяжести приведенного сечения.
относительно центра тяжести приведенного сечения.
При длительном действии усилия предварительного обжатия выгиб балки вследствие ползучести и усадки возрастает на величину 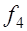 , а значит возрастает и кривизна элемента на соответствующую величину
, а значит возрастает и кривизна элемента на соответствующую величину 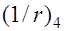
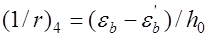 , (26.10) где
, (26.10) где 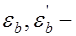 относительные деформации бетона, вызванные его усадкой и ползучестью от усилия предварительного обжатия. Определяемые соответственно на уровне центра тяжести растянутой продольной арматуры и крайнего сжатого волокна бетона по формулам:
относительные деформации бетона, вызванные его усадкой и ползучестью от усилия предварительного обжатия. Определяемые соответственно на уровне центра тяжести растянутой продольной арматуры и крайнего сжатого волокна бетона по формулам:
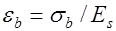 ;
; 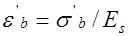 , (26.11) где
, (26.11) где 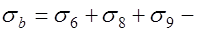 сумма потерь предварительного напряжения от усадки и ползучести бетона для арматуры, расположенной при эксплуатации в растянутой зоне;
сумма потерь предварительного напряжения от усадки и ползучести бетона для арматуры, расположенной при эксплуатации в растянутой зоне; 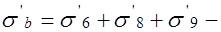 то же, но для напрягаемой арматуры, расположенной в сжатой зоне.
то же, но для напрягаемой арматуры, расположенной в сжатой зоне.
После приложения длительных и постоянных нагрузок балка получает прогиб 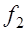 с соответствующей кривизной оси
с соответствующей кривизной оси 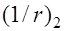 . От кратковременного действия нагрузок балка получит дополнительный прогиб
. От кратковременного действия нагрузок балка получит дополнительный прогиб 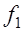 , соответствующий кривизне
, соответствующий кривизне 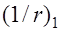 . Таким образом, полный прогиб и полная кривизна балки от всех действующих на нее силовых факторов составят
. Таким образом, полный прогиб и полная кривизна балки от всех действующих на нее силовых факторов составят
 |
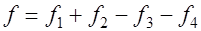 ;
; 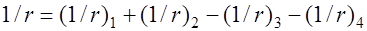 .
.
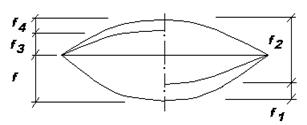 |
Рис. 26.1 Рис.26.2
| <== предыдущая лекция | | | следующая лекция ==> |
| РАСЧЕТ ПО ОБРАЗОВАНИЮ ТРЕЩИН В ИЗГИБАЕМЫХ И ВНЕЦЕНТРЕННО ЗАГРУЖЕННЫХ ЭЛЕМЕНТАХ | | | ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ ЖБК ЗДАНИЙ И СООРУЖЕНИЙ |
Дата добавления: 2018-09-24; просмотров: 713;
