Определение структуры продукции с учетом лимитирующего фактора
Рассмотрим приведенный выше пример, но пусть производственные возможности "Фирмы" составляют не 1500 штук, а 1000 пачек бумаги в месяц. В этом случае для принятия спецзаказа в 500 пачек нужно сократить на 500 пачек существующие заказы. Возмещение постоянных расходов нужно производить за счет всех единиц продукции, в том числе и спецзаказа, т.е. все расходы являются релевантными. Применим маржинальный подход.
| Показатели | Существующие заказы на 500 пачек, руб. | Спецзаказ на 500 пачек, руб. | Итого, руб. |
| 1. Реализация 2. Затраты: – прямые материалы – прямая зарплата – переменные общепроизводственные – переменные издержки реализации | 20 × 500 = 10000 | - | |
| Итого переменных затрат | 6000 | 5500 | 11500 |
| 3. Маржинальная прибыль 4. Постоянные общепроизводственные расходы 5. Постоянные общехозяйственные | |||
| Прибыль от реализации | 0 |
Предложение явно невыгодно, т.к. вместо существующей прибыли 3 руб. на 1 пачку × 1000 пачек = 3000 руб. "Фирма" будет иметь 0 руб.
Вывод: при принятии решений о производстве следует учитывать наличие ограничивающего фактора.
При планировании производственной программы в условиях ограниченных производственных мощностей (например, человеко-часов или машино-часов) выбирают структуру выпуска, т.е. какие продукты и в каких объемах производить для максимальной прибыли.
Для выбора из альтернативных вариантов используем метод приростного анализа при маржинальном подходе.
Пример. Фирма может выпускать продукт А и продукт Б. Маржинальные калькуляции единицы этих продуктов:
| № п/п | Показатели | Усл. обозна-чения | На единицу продуктов, руб. | |
| А | Б | |||
| 1. | Цена | В' | ||
| 2. | Переменные расходы | З'2 | ||
| 3. | Удельная маржинальная прибыль | М' | ||
| 4. | Норма маржинальной прибыли
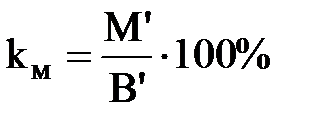
| kм | 30% | 40% |
Продукт "Б" приносит бóльшую маржинальную прибыль и именно его следует запустить в производство, но это при условии, что нет лимитирующего фактора, что на практике встречается редко. Поэтому рассчитывают норму маржинальной прибыли не на единицу выручки, а на единицу ограничивающего фактора.
Пусть в нашем примере производственные мощности ограничены 2000 машино-часами и за 1 час можно произвести 4 штуки продукта А или 1 штуку продукта Б. Проведем анализ с учетом этой информации.
| № п/п | Показатели | Продукт "А" | Продукт "Б" |
| 1. | Маржинальная прибыль на единицу продуктов (на 1 штуку) (из предыдущей таблицы, п.3), руб. | ||
| 2. | Количество единиц продукции, производимых за 1 машино-час, шт. | ||
| 3. | Маржинальная прибыль на 1 машино-час, руб. | ||
| 4. | Маржинальная прибыль за 1000 машино-часов, руб. |
Выбор следует сделать в пользу продукта "А", т.к. наибольшая прибыль получается в случае его производства и продажи.
Вывод: в условиях ограниченного ресурса критерием максимизации прибыли является наибольшая маржинальная прибыль на единицу этого ресурса.
В реальной жизни действуют не один, а несколько лимитирующих факторов. Тогда для принятия решений по определению ассортимента продукции, дающего наибольшую прибыль, используют методы линейного программирования (уравнений, графический, "проб и ошибок", матричный и т.д.).
Дата добавления: 2018-09-24; просмотров: 677;
