Общие и частные свойства композиции распределений.
Общими называют такие свойства композиций распределений, которые не зависят от вида исходных законов распределения, составляющих композицию. Это следующие свойства:
1. Математическое ожидание случайной величиныYравно арифметической сумме математических ожиданий случайных величин, законы распределения которых составляют композицию распределений:
M[Y]=M[X1]+ M[X2]+ M[X3]+ …+ M[Xn]
2. Дисперсия случайной величины Y равна арифметической сумме дисперсий случайных величин, законы распределения которых составляют композицию распределений:
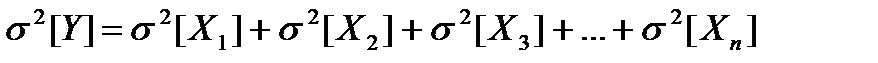
Из этих свойств можно сделать два вывода:
1) с ростом числа изделий п в выборке коэффициент вариации убывает, а следовательно, мера точности возрастает пропорционально 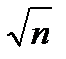
2) если имеются две (или более) случайные величины с резко отличными средними квадратическими отклонениями, то в композиции их распределений случайная величина с меньшей дисперсией практически не оказывает влияния на суммарную дисперсию.
Частные свойства композиции распределений зависят от конкретного вида исходных законов распределения, составляющих композицию. Предположим, что случайные величины Х1 и Х2 имеют распределения, описываемые экспоненциальными законами с одним и тем же параметром l:
M[X1]=M[X2]=l/l; s[X1]= s[X2]= l/l.
Рассмотрим, будет ли композиция этих законов также описываться экспоненциальным законом распределения. Согласно первому общему свойству для Y=X1+X2,
M[Y]=M[X1]+ M[X2]=1/l+1/l=2/l
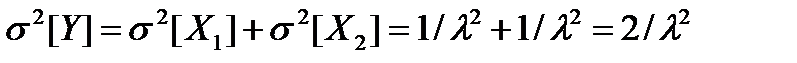
Тогда коэффициент вариации
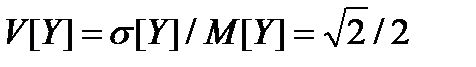
В результате композиции двух экспоненциальных распределений новое распределение не подчиняется экспоненциальному закону, при котором коэффициент вариации всегда равен единице. Если взять два распределения Вейбулла, то в композиции не получится распределение Вейбулла. То же можно сказать и о других законах распределения, за исключением законов Пуассона и Гаусса.
При большом числе распределений любого вида распределение их композиции близко к гауссовскому. Более того, в результате композиции большого числа неодинаковых распределений независимых случайных величин с различными, но не очень сильно отличающимися друг от друга дисперсиями и математическими ожиданиями получается также гауссовское распределение.Этоположение теории вероятностей называется центральной предельной теоремой, которая определяет особую роль гауссовского распределения в теории вероятностей.[9]
Композиция распределения встречается на практике при обобщении результатов испытаний нескольких выборок, взятых из различных партий изделий.
Предположим, что на испытания предъявляется партия, состоящая из N изделий. Из них для N1 изделий плотность вероятности случайной величины Х составляет f1(X), а для N2 изделий — f2(X). Например, когда партию изделий, предъявляемых заказчику, комплектуют из однотипных изделий, изготовленных из различных партий сырья и полуфабрикатов или на различных технологических линиях. В этом случае получается суперпозиция распределений f1(X) и f2(X):
f(Y)=w1f1(X)+ w2f2(X)
где w1 =N1/N; w2 =N2/N.
Математическое ожидание и дисперсия случайной величины Y в суперпозиции распределений определяются выражениями
M[Y]=w1M1[X]+ w2M2[X]
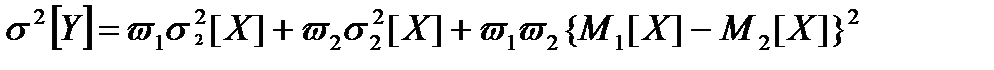
Дата добавления: 2017-02-20; просмотров: 962;
