Статистический ряд и его характеристики.
Основные понятия.
Предположим, что в партии изделий производят замер какого-либо параметра, конкретное значение xi которого для каждого изделия является случайным. В результате замеров получают совокупность случайных значений параметров. Если расположить эти значения в возрастающем порядке, то образуется упорядоченный, или ранжированный, ряд случайных значений xi. В таком ряду повторяющиеся два (или более) раза значения xi объединяют. Число повторяющихся значений обозначают через mi и называют абсолютной частотой или статистическим весом, а сам ряд значений случайной величины - статистическим рядом.
Статистический ряд имеет две важнейшие характеристики, которые в сжатой форме достаточно полно отражают результаты измерений. Одна из них описывает среднее положение наблюдаемых значений, а другая – отклонения отдельных значений от среднего. Среднее положение наблюдаемых значений в ряду характеризуется с помощью среднего арифметического и медианы. Для простой статистической совокупности, в которой каждое значение случайной величины встречается только один раз, среднее арифметическое
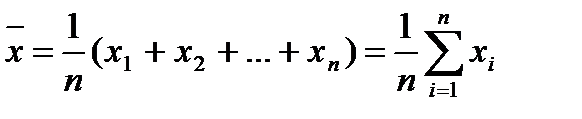
Для статистического ряда, в котором каждому значению Xi случайной величины соответствует некоторая частота mi, среднее арифметическое
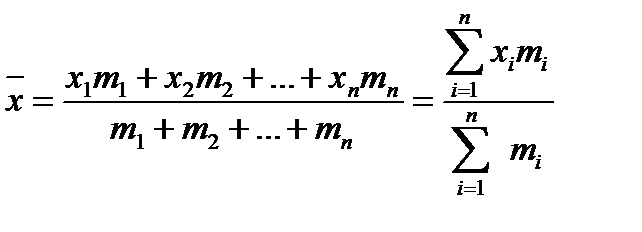
В этом случае среднее арифметическое 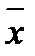 называют средним взвешенным значением случайной величины. Величина
называют средним взвешенным значением случайной величины. Величина 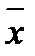 только тогда является обобщающей характеристикой, когда она применяется к однородной совокупности наблюдаемых значений одной и той же случайной величины.
только тогда является обобщающей характеристикой, когда она применяется к однородной совокупности наблюдаемых значений одной и той же случайной величины.
Медианой случайной величины Х называют такое ее значение Me, которое приходится на середину упорядоченного ряда, т.е. медиана делит упорядоченный ряд на две равные по числу случайных значений группы. При чётном числе измерений медиана равна среднему арифметическому двух соседних значений, расположенных в середине ряда; при нечётном числе измерений – значению случайной величины, занимающему срединное положение в ряду.
Характеристики 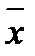 и Me не учитывают рассеивание около них отдельных значений случайной величины. Для описания рассеивания значений случайных величин применяют ряд характеристик. Простейшей из них является размах
и Me не учитывают рассеивание около них отдельных значений случайной величины. Для описания рассеивания значений случайных величин применяют ряд характеристик. Простейшей из них является размах
R=xmax-xmin
где xmax и xmin — максимальное и минимальное значения случайной величины. Размах служит для приблизительной оценки рассеивания значений случайной величины. В качестве меры колебания значений случайной величины в статистическом ряде наиболее часто применяют средний квадрат отклонения, который называют выборочной дисперсией
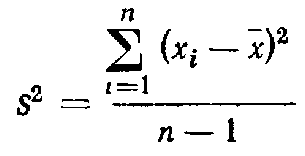
При наличии соответствующих частот mi вычисляется взвешенная выборочная дисперсия:
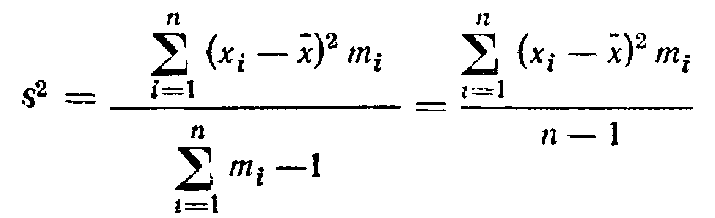
Дисперсия имеет размерность квадрата случайной величины. Это не всегда удобно и не наглядно, отвлечено от физического смысла. Для наглядной характеристики рассеивания служит среднее квадратическое отклонение, размерность которого совпадает с размерностью измеряемой случайной величины:
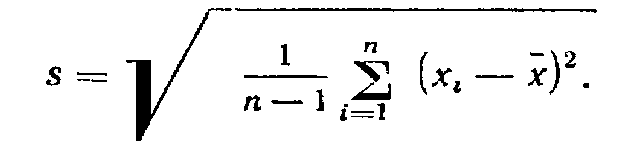
Если известны соответствующие частоты распределения mi, то взвешенное среднее квадратическое отклонение
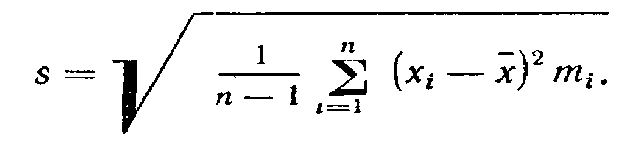
Для характеристики рассеивания случайной величины используют также коэффициент вариации Vi,, равный отношению ее среднего квадратического отклонения к среднему арифметическому значению и выражаемый в процентах или долях единицы:
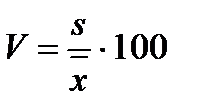
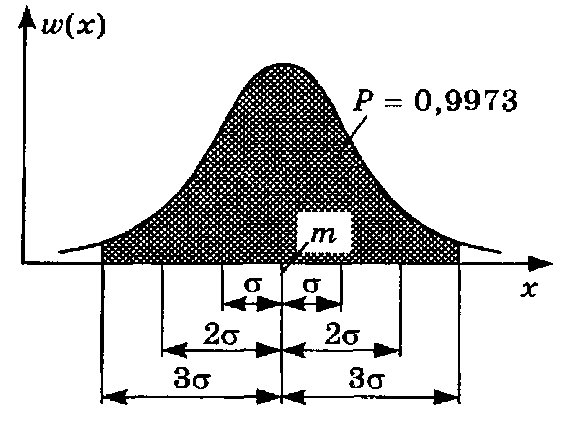
в диапазон 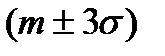 укладывается практически все рассеивание параметра (»99,7% значений). Поэтому на практике, определив параметры нормальной модели, предельными значениями рассматриваемого параметра считают точки, отстоящие от величины т на ±3s. Такой способ оценки предельных отклонений параметра получил название "правила трех сигм".
укладывается практически все рассеивание параметра (»99,7% значений). Поэтому на практике, определив параметры нормальной модели, предельными значениями рассматриваемого параметра считают точки, отстоящие от величины т на ±3s. Такой способ оценки предельных отклонений параметра получил название "правила трех сигм".
Для оценки точности какого-либо процесса при действии систематической составляющей погрешности используют коэффициент смещения
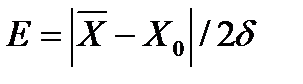
Случайные величины могут быть дискретными или непрерывными. Соответственно и распределения их вероятностей описываются законами распределения дискретных или непрерывных случайных величин. Пример дискретной случайной величины — число изделий в выборке, параметры которых не отвечают тем или иным требованиям. Число дефектных изделий может быть только целым. Пример непрерывной случайной величины — время работы изделия до отказа, которое может принимать и дробные значения. Распределение вероятностей появления дискретных случайных величин чаще всего описывается гипергеометрическим или биномиальным законом или законом Пуассона; распределение вероятностей появления непрерывных случайных величин - экспоненциальным или гауссовским законом, а также законом Вейбулла.
Для решения многих инженерных задач надо располагать вероятностным описанием параметров. В ряде случаев такое описание может быть косвенно получено из технической документации на элементы, устройства или процесс.
Дата добавления: 2017-02-20; просмотров: 2534;
