Определение коэффициентов влияния

Коэффициенты влияния зависят от вида математической модели ЭУ и номинальных значений первичных параметров. При заданном виде модели и выбранных номинальных значениях первичных параметров, коэффициенты влияния первичных параметров являются детерминированными величинами, т.е. представляют собой фиксированные числа. Коэффициент влияния может быть как положительным, так и отрицательным, как больше единицы, так и меньше единицы.

На практике для определения коэффициентов влияния используют две группы методов:

а) расчётно-аналитические;

б) экспериментально - расчётные.

Коэффициент влияния В; i-го первичного параметра при аналитических методах может быть подсчитан с помощью выражения.

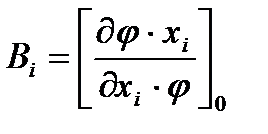
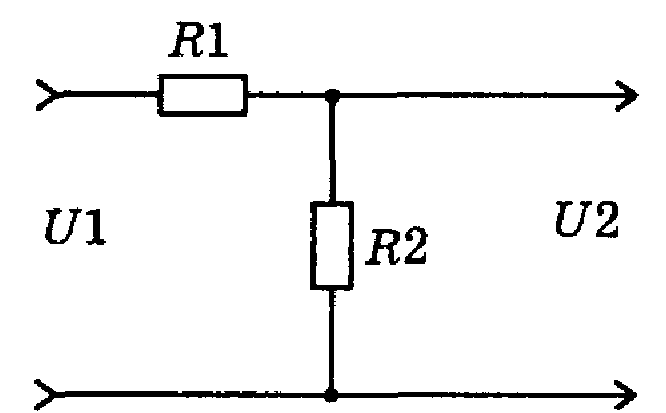
Пример. Определим коэффициенты влияния резисторов R1 и R2 делителя напряжения (рис.), рассматривая в качестве выходного параметра у коэффициент деления делителя К_Д

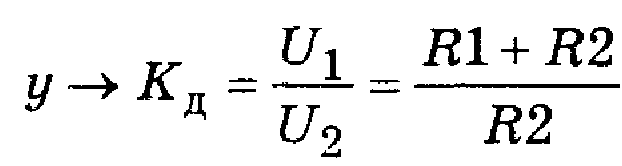
Пусть:

R1 = 2 кОм ± 5%; R2 = 3 кОм ± 5%;

Воспользуемся формулой для коэффициента деления. Принимая во внимание, что (j ®К_Д, x_i® R_i (i=1; 2)), получим

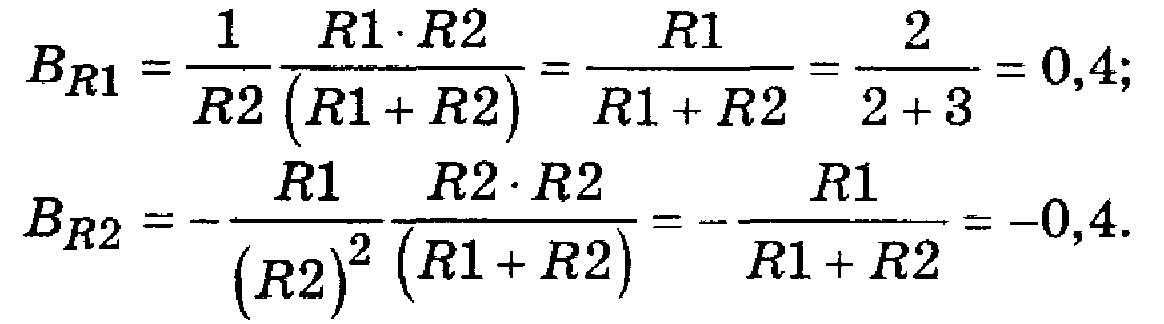
Пример. Определим коэффициенты влияния параметров R и С, RС- цепи, выходным параметром которой является постоянная времени t = RC.

Решение. В данном примере j(x) —> t = RC.

С учетом этого, определяем

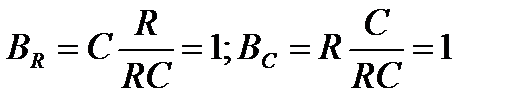
Если выходной параметр у может быть представлен в виде выражения

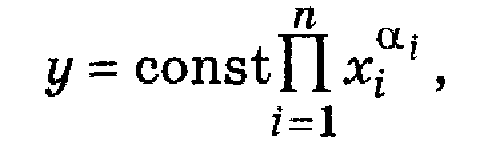
то коэффициенты влияния могут быть определены как Bi =a_i, i=1,..., n.

Пример. Определим коэффициенты влияния параметров L и С колебательного контура, рассматривая в качестве выходного параметра у резонансную частоту контура fрез. Пусть значения параметров L и С:

L=10мкГн±10%; С=100пФ±5%.

Решение. В данном случае у —> fрез

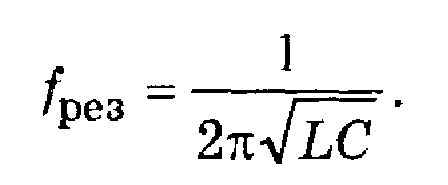
Это выражение можно представить в виде

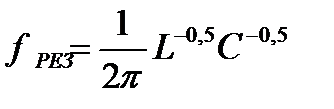
Из последней записи видно, что

В_L= -0,5; B_C =- -0,5.

Если выходной параметр у может быть представлен в виде отношения

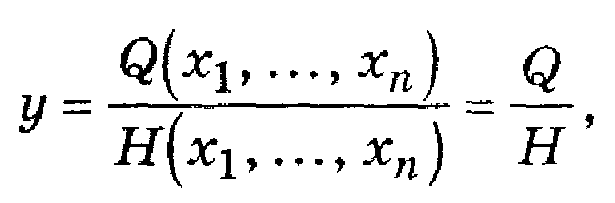
гдеQ, Н — многочлены, содержащие не обязательно все х_i, причём их степень может быть любой, то коэффициент влияния i-го первичного параметра может быть подсчитан с помощью выражения

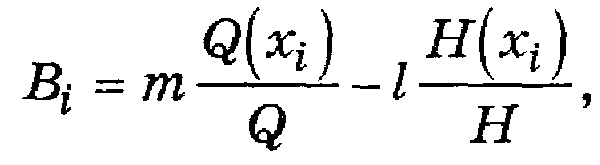
где Q(Xi) и H(Xi) — части многочленов Q и Н, содержащие только х_i;

т, l — максимальные степени х_i, соответственно в многочленах Q(х_i) и Н(х_i)

Пример. Определим с помощью последней формулы коэффициенты влияния резисторов R1 и R2 рассмотренного делителя напряжения.

Решение. Ранее было принято, что j ®К_Д,. Можно записать

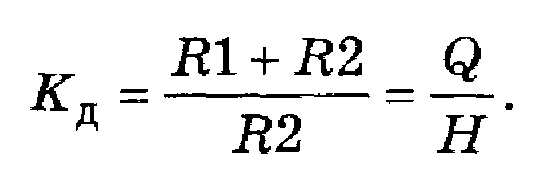
В данном случае: Q = R1 + R2, Н = R2.

При выборе, например, в качестве х_i параметра R1

Q(R1)=R1; H(R1)=0: m=1; l=0

Следовательно

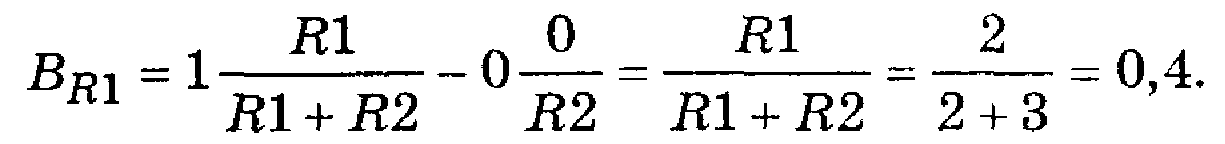
Этот результат, как видим, совпадает с результатом, полученным ранее другими способами

Коэффициенты влияния могут быть также определены методом приращений. В этом случае пользуются формулой

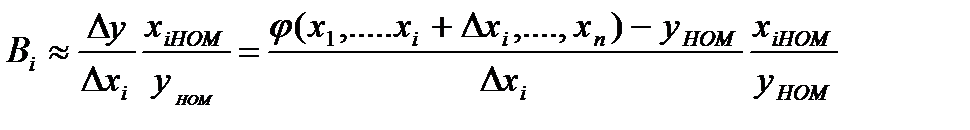
Точность определения коэффициента В_i тем меньшая, чем сильнее выражено нелинейное влияние первичного параметра x_i на выходной параметр у и чем больше задаваемое приращение Dx_i.

Пример. Определим коэффициент влияния резистора R2 рассмотренного делителя напряжения, считая выходным параметром коэффициент деления.

Решение. Напомним, что в условиях этого примера

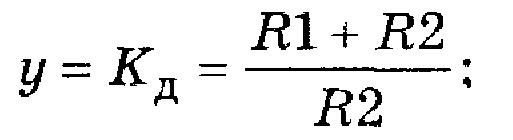
R1 = 2 кОм ± 5%; R2 = 3 кОм ± 5%;

Для определения коэффициента влияния В_R2 первичному параметру R2 дадим малое приращение DR2 =0,1 кОм. Получим

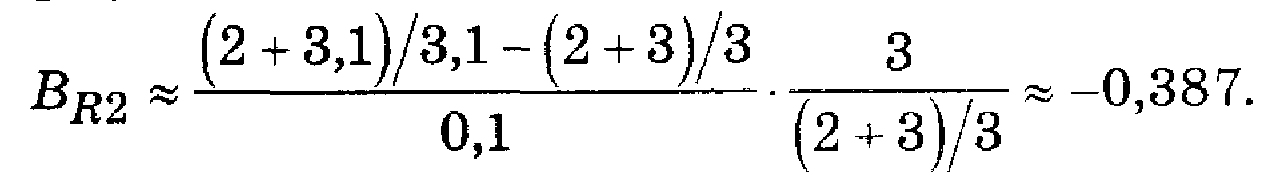
Этот результат несколько отличается от результата, полученного в предыдущих примерах (В_R2 = -0,4).