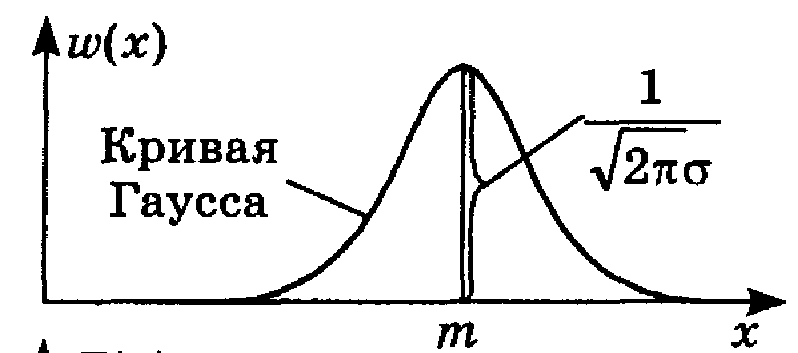
Модели законов распределения параметров

Истинный закон распределения параметра может быть не известен, поэтому часто используют некоторое приближение этого закона, полученное экспериментально – "модель закона распределения параметра". Известно более 300 видов моделей законов распределения. На практике при проектировании РЭУ используют не более 20. Широко используют нормальную и усеченную нормальную; равномерную; экспоненциальную; логарифмически нормальную; модель Вейбулла.

Нормальная модель

Функция w для этой модели имеет вид

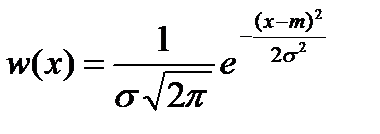
где х – рассматриваемый параметр и его текущие значения;

т, s – параметры модели.

Функция распределения для нормальной модели может быть получена в виде интеграла, который нельзя выразить через элементарные функции. Для его определения используют специальные табличные функции.

Функция распределения параметра х в случае нормальной модели запишется как

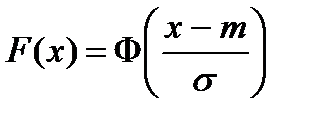
Тогда вероятность вида Р(а £ х £ b) может быть определена как

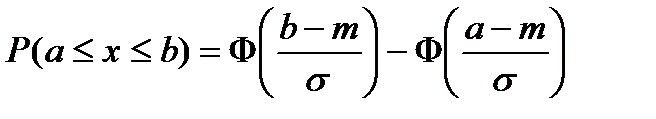
Только для нормальной модели справедливы равенства:

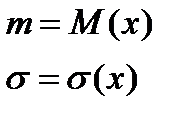
В случае нормального распределения практический интерес представляет вопрос, какова вероятность вида

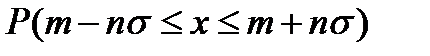
где n = 1, 2, 3, …-- целые числа

Используя выражение для Р, для n= 1, 2, 3 можно получить:

	n= 1	n= 2	n= 3
	0,68	0,95	0,997

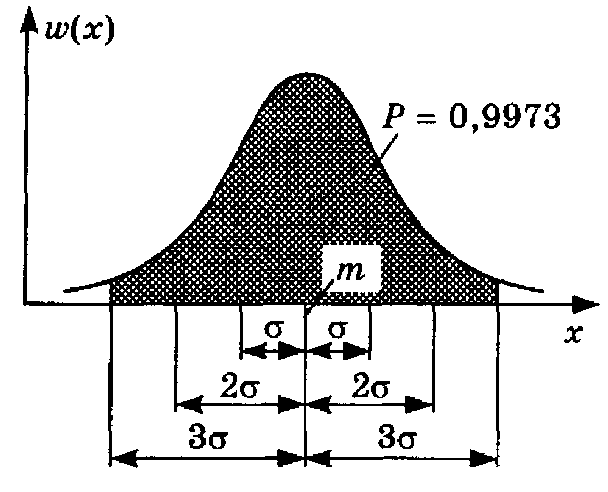Из таблицы видно, что в диапазон 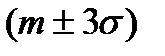укладывается практически все рассеивание параметра (»99,7% значений). Поэтому на практике предельными значениями рассматриваемого параметра считают точки, отстоящие от величины т на ±3s.

Этот способ оценки предельных отклонений параметра получил название "правила трехтрёх сигм". Экспериментально подтверждается, что для резисторов, конденсаторов и др. электронных приборов с допуском более ±10% оправдано использование нормальной модели, следовательно, и правило "трехтрёх сигм". Этим правилом пользуются при установлении допусков на параметры электронных элементов