Магнитная нейтронография

Согласно квантовой механикe магнитный момент частицы или системы частиц пропорционален их механическому моменту (моменту количества движения) и электрическому заряду:

μ= g (q/2mc)∙J, (8.1)

где g – фактор Ланде (g = 1 для орбитального момента, g = 2 для собственного (спинового) момента), q – электрический заряд, m – масса частицы, с – скорость света, J – механический момент (орбитальный или спиновый).

Механический момент квантуется, т.е. его проекция на ось квантования может принимать только дискретные значения от -ћJ_z до +ћJ_z. Для орбитального момента J_z –целое число l, т.е. -ћl, -ћ(l-1), -ћ(l-2),… ≤ J_z ≤ …, ћ(l-2), ћ(l-1), ћl. Для спинового момента J_z может быть целым для бозонов или полуцелым для фермионов (при нечетном числе частиц).

Модуль (величина) механического момента всегда больше, чем его максимальная проекция, а именно

J² = J(J+1) или J = ћ[l(l+1)]^1/2. (8.2)

Т.е. вектор J всегда отклонен от оси квантования на некоторый угол. Это следствие принципа неопределенности – все три компоненты момента не могут быть определены одновременно, а если бы момент был направлен строго по оси z, то проекции на две другие оси были бы равны 0. Часто под магнитным моментом понимают именно максимальное значение проекции. Какая на самом деле величина должна быть использована – полный момент или его проекция – зависит от конкретной физической задачи. Например, в выражение для магнитной восприимчивости входит полный момент, т.е. |J| = [J(J+1)]^1/2, а в сечение когерентного нейтронного рассеяния – максимальная проекция момента.

8.1. Магнитные свойства электрона, нейтрона, атома, вещества.

Для электрона g = 2, q = e, J_z = s = ћ/2 и, следовательно

μ_е= (eћ/2m_еc) = μ_B, (8.3)

где μ_B = 9.274×10^-21 эрг/гс – магнетон Бора (в системе СГС). Учет радиационных поправок в квантовой электродинамике приводит к незначительному изменению величины магнитного момента электрона, а именно μ_е= μ_B(1+a/2p-…), где a = e²/ħc » 1/137 – постоянная тонкой структуры. Еще раз подчеркнем, что μ_е= μ_B есть значение максимальной проекции спинового магнитного момента на ось квантования. Полная величина магнитного момента соответствует |s| = ћ[1/2(1/2+1)]^1/2 = ћ√3/2.

В стандартной теории Дирака магнитный момент нейтрона должен быть равен нулю, т.к. отсутствует электрический заряд. Однако из эксперимента следует, что магнитный момент нейтрона отличен от нуля и есть

μ_n= -1.91321(5) (eћ/2m_pc), (8.4)

где величина μ_N= (eћ/2m_pc) называется ядерным магнетоном, причем m_p – масса протона. Здесь надо иметь в виду, что выражение для μ_N записано в системе единиц СГС, в системе СИ μ_N= (eћ/2m_p) и, так же как для электрона, величина момента является максимальной проекцией на ось квантования. Ненулевая величина магнитного момента нейтрона (его называют аномальным) связана с его сложной внутренней структурой. Известно, что хотя полный электрический заряд нейтрона равен нулю, среднеквадратичный радиус его распределения отличен от нуля.

Магнитный момент атома пропорционален его полному механическому моменту, который складывается из орбитального момента L и спинового момента электронов S, т.е. J = L+S, причем L есть векторная сумма всех орбитальных моментов электронов, S – векторная сумма всех спиновых моментов электронов. Аналогично, проекция J_z есть сумма проекций L_z и S_z. Фактор Ланде, который используется при пересчете механического момента в магнитный, в этом случае есть:

g = 1 +[J(J+1) + S(S+1) – L(L+1)] / [2J(J+1)]. (8.5)

Если L = 0, то J = S и g = 2, если S = 0, то J = L и g = 1. Итак, для атома μ= gμ_B(L +S).

В соответствии со сказанным выше, как правило, под магнитным моментом атома понимают величину его проекции на ось квантования:

μ_A= g j μ_B, (8.6)

где j – максимальное значение проекции полного момента (в единицах ћ) на ось квантования. Для атомов с заполненными оболочками L = S = 0 и магнитный момент отсутствует. Для большинства магнитных атомов L ≈ 0 и магнитный момент определяется спиновым моментом. Соответственно, если имеется n нескомпенсированных спинов, то

μ_A= 2nsμ_B = nμ_B. (8.7)

Полный момент атома при L = 0 и наличии n нескомпенсированных спинов есть |μ_A|= [n(n+2)]^1/2μ_B.

8.2. Магнитные структуры кристаллов.

Говорят, что кристалл обладает магнитной структурой или дальним магнитным порядком, если есть какая-либо закономерность в направлениях магнитных моментов атомов. В кристалле, находящемся в диамагнитном или парамагнитном состоянии, дальний порядок в направлениях моментов отсутствует. В кристаллах с упорядоченными моментами выделяют тип коллинеарных магнетиков, к которым относят ферро- (ФМ), антиферро- (АФМ) и ферримагнитные состояния. Существует много вариантов неколлинеарныхмагнетиков, в которых магнитные моменты упорядочены некоторым сложным образом, например, по спирали. Периоды упорядочения неколлинеарных структур могут быть несоизмеримы с периодами кристаллической решетки.

Напомним для полноты, что к диамагнетикам относятся вещества, атомы которых не обладают постоянным магнитным моментом, их магнитная восприимчивость отрицательна и не зависит от температуры. Диамагнетизм является универсальным свойством, т.е. все вещества в той или иной степени его проявляют. Магнитный момент диамагнетика возникает только при действии магнитного поля, т.е. является наведенным и весьма мал по величине. Парамагнетики - вещества, какие-либо атомы в которых обладают постоянным магнитным моментом. Под воздействием поля моменты ориентируются по полю, т.е. магнитная восприимчивость положительна, ее зависимость от температуры выражается законом Кюри-Вейса. При понижении температуры парамагнетик зачастую переходит в магнитоупорядоченное состояние. В ферромагнитныхвеществах без воздействия внешнего магнитного поля при некоторой температуре (температуре Кюри, T_C) возникает состояние с постоянной намагниченностью. Моменты всех магнитных атомов направлены в одну сторону, по крайней мере, в пределах одного домена. Антиферромагнетики - вещества, которые без воздействия внешнего поля переходят при понижении температуры (при температуре Нееля, T_N) в состояние с упорядоченным расположением моментов. Намагниченность отсутствует, т.к. в целом моменты упорядочены антипараллельно и полностью компенсируют друг друга. Возможно несколько вариантов упорядочения. Наконец, ферримагнетиками называются вещества с АФМ расположением моментов, но из-за разной величины моментов в разных позициях полная компенсация отсутствует и некоторая намагниченность имеется. Схематически основные типы магнитных структур изображены нарис. 8-1.

8.3. Описание магнитных структур.

Способы описания магнитной структуры, как правило, различаются для коллинеарных и неколлинеарных структур, а также для соразмерных и несоразмерных структур. В случае соразмерной коллинеарной структуры задается элементарная магнитная ячейка, в которой известны атомы, обладающие ненулевым магнитным моментом, величина моментов и их направление относительно осей элементарной ячейки. Связь между направлениями моментов какого-то исходного атома в “0”-ячейке и атома в n-й (кристаллографической) ячейке задается соотношением:

S_n = S₀·exp(2πiKT_n), (8.8)

где T_n - вектора трансляции (T = n₁a₁+ n₂a₂ + n₃a₃), набор которых включает и вектора центрирующих ячейку узлов, K – называется вектором магнитной структуры (вектором МС) или вектором распространения. Вектор K определен в обратной решетке, т.е. K = K₁b₁+ K₂b₂ + K₃b₃. Для ФМ структуры K= 0, все моменты направлены одинаково. АФМ чередование направления моментов вдоль базисного направления, т.е. условие S_n = -S₀ при n нечетном, задается вектором типа K= (1/2, 0, 0). Соответственно, чередование вдоль обоих направлений в плоскости задается вектором типа K= (1/2, 1/2, 0), чередование по всем трем базисным направлениям задается вектором K= (1/2, 1/2, 1/2).

Если магнитная структура несоразмерна с атомной, элементарную магнитную ячейку ввести невозможно. В этом случае большинство известных спиральных структур удается описать с помощью соотношения, задающего момент в n-й ячейке кристалла через момент в некоторой исходной ячейке:

S_n = S₀exp(2πiKT_n) + S₀*exp(-2πiKT_n), (8.9)

где T_n – вектор трансляции, связывающий эти ячейки, S₀ и S₀*– комплексно сопряженные величины. В отличие от соразмерных структур, компоненты вектора Kв (8.9) – произвольные числа.

Возникновение соразмерного магнитного порядка (при понижении температуры) приводит к появлению магнитного вклада в существующие (ядерные) пики (при K= 0) или к появлению новых дифракционных пиков в пределах элементарной ячейки в обратном пространстве. Во втором случае, координаты вектора K означают появление магнитного пика (или магнитного вклада) в соответствующей точке обратной решетки. Например, при образовании АФМ чередовании направления момента по всем трем периодам (G-структура) появится дифракционный пик в точке (1/2, 1/2, 1/2).

Часто встречающаяся несоразмерная синусоидальная модуляция приводит к появлению так называемых сателлитов, располагающихся рядом с ядерными пиками. Рассмотрим в качестве иллюстрации рассеяние на одномерной периодической структуре (период Т₁) с гармонически модулированной (период Т₂) величиной магнитного момента. Распределение рассеивающей плотности можно записать в виде:

b(x) = b₀ [1 + α cos(2πx/T₂)]· 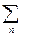δ(x – nT₁), (8.10)

где b₀ – средняя амплитуда рассеяния, α – амплитуда модуляции, сумма δ-функций фиксирует положения атомов. В соответствии с общими свойствами фурье-преобразований структурный фактор произведения двух функций есть свертка соответствующих структурных факторов. Т.е. надо вычислить свертку функций f₁ и f₂, где

f₁ = òb₀(x) exp(2πi xξ) dx = 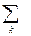δ(ξ – k/T₁), (8.11)

f₂ = b₀ ò [1 + α cos(2πx/T₂)] exp(2πi xξ) dx =

= b₀ [δ(ξ) + α/2 δ(ξ+1/T₂) + α/2 δ(ξ-1/T₂)]. (8.12)

Свертка (8.11) и (8.12) дает:

F(ξ) = b₀ 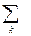[δ(ξ – k/T₁) + α/2 δ(ξ – k/T₁ + 1/T₂) + α/2 δ(ξ – k/T₁ - 1/T₂)], (8.13)

т.е. в обратном пространстве имеются основные линии (первое слагаемое в квадратных скобках), расположенные с периодом 1/Т₁, рядом с которыми на расстоянии 1/Т₂ справа и слева имеются пики с амплитудой α/2. При Т₂>>Т₁ сателлиты располагаются близко к основным пикам. Для вычисления эффекта негармонической модуляции ее следует разложить в ряд Фурье, повторить предыдущие рассуждения и убедиться, что появляются несколько сателлитов с постепенно уменьшающимися амплитудами.

Для симметрийного описания соизмеримых магнитных структур к стандартным кристаллографическим операциям, с помощью которых образуются 230 пространственных групп симметрии, добавляется специфическая операция антисимметрии, с помощью которой направление магнитного момента изменяется на противоположное. В результате возникает 1651 пространственная группа, которые называют черно-белыми или шубниковскими группами (А.В.Шубников, 1951).

Альтернативный подход описания магнитной структуры кристаллов основан на теории неприводимых представлений (НП) пространственных кристаллографических групп (Ю.А.Изюмов, 1980). Схема этого подхода состоит в следующем. Формула (8.8) заменяется на более общую

S_n = 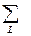C_Lexp(2πiK_LT_n)S₀, (8.14)

где введена совокупность векторов K_L, получающаяся из вектора МС действием элементов симметрии кристаллографической группы G, T_n вектор трансляции, связывающий исходную и n-ю ячейки. Говорят, что (8.14) определяет звезду волнового вектора, содержащую L лучей. Коэффициенты смешивания C_L называют каналом перехода, они определяют одну из 36 решеток шубниковской симметрии. Для определения ориентации и величины магнитных моментов вводится разложение M₀ по базисным функциям НП группы G. Далее предполагается (в духе теории Ландау фазовых переходов второго рода), что магнитный фазовый переход, при котором возникла магнитная структура, происходит только по какому-то одному НП, т.е.

S₀ = 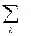C_λ^ν S_λ^ν, (8.15)

где индекс ν задает номер НП и считается фиксированным, M_λ^ν – базисные функции НП. В вариационной процедуре участвуют коэффициенты C_λ^ν, которых, как правило, немного (от 1 до 6). Неприводимое представление, по которому прошел фазовый переход, заранее неизвестно, поэтому проверяются все возможные.

8.4. Магнитное рассеяние нейтронов.

Если магнитные моменты атомов не упорядочены по направлениям, то магнитное сечения рассеяния (некогерентного) неполяризованных нейтронов на таком кристалле есть:

dσ/dΩ = 2/3(r₀γ)²∙S²∙P²(Q), (8.16)

где r₀ = e²/m_ec² – классический радиус электрона, е – заряд электрона, m_e – масса электрона, с – скорость света, γ = -1.913 – аномальный магнитный момент нейтрона (в ядерных магнетонах), S² = S_z(S_z+1), S – спин атома, P(Q) – магнитный формфактор атома (формфактор спиновой плотности), являющийся Фурье-преобразованием от распределения спиновой плотности электронов,Q – вектор рассеяния. Как правило, P(Q) имеет форму, близкую к гауссовой, т.е. интенсивность некогерентного парамагнитного рассеяния максимально при малых Q и плавно спадает с ростом Q.

Когерентное рассеяние возникает, если в магнитные моменты атомов кристалла каким-либо образом упорядочены по направлениям. Далее разбирается только простейший случай коллинеарной магнитной структуры, т.е. ситуация, когда моменты всех магнитных атомов параллельны с точностью до знака.

В разделе 2.2.2 было показано, что когерентная амплитуда магнитного рассеяния на атоме, входящему в такую магнитную структуру есть:

f_m,j = 2e²γ/(m_ec²)∙P_j(Q)∙S_j∙|m – e (m·e)|, (8.17)

где γ – аномальный магнитный момент нейтрона, P_j(Q) – магнитный формфактор атома, здесь предполагаемый изотропным, S_j – спин j-го атома в единицах ћ в смысле максимальной проекции на ось квантования, m – единичный вектор в направлении момента атома, e= Q/Q = H/H – единичный вектор рассеяния.

Пользуясь (8.17), выражение для магнитного структурного фактора на коллинеарной структуре можно записать в виде, аналогичном (3.11), а именно

F_{H, mag} = M_hkl 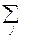S_j×μ_j× exp(2piHr_j)∙exp(-W_j), (8.18)

где сумма берется по всем магнитным атомам (с координатами x_j, y_j, z_j) в ячейке, M_hkl = |m – e·(m·e)| = |sin η|, η – угол между направлением магнитных моментов атомов m и вектором e, μ_j = 2e²γ/(m_ec²)∙P_j(Q). Подстановка констант и запись F_{H, mag} в единицах 10^-12, приводит к μ_j = 0.539P_j(Q). В этой формуле предполагается, что магнитные моменты всех атомов направлены одинаково с точностью до знака, который учитывается знаком величин S_j.

Для неполяризованного пучка нейтронов ядерная и магнитная интенсивности складываются квадратично, т.к. интерференционный член исчезает вследствие равного присутствия положительного и отрицательного вкладов, т.е.

I_hkl ~ çF_hkl, _nuc ç² + çF_hkl, _mag ç². (8.19)

Эта формула является основой для анализа магнитной структуры, если эксперимент проведен с монокристаллом. Если же эксперимент проведен с поликристаллом (как правило, используется именно этот вариант), то множитель M_hkl² в магнитном структурном факторе необходимо усреднить по эквивалентным наборам индексов Миллера. При этом в высокосимметричных структурах возникает неоднозначность ориентации момента относительно кристаллографических осей, связанная с тем, что пики с разными индексами Миллера имеют одинаковые d_hkl. Например, для кубической сингонии невозможно определить, вдоль какой из осей направлен момент, т.к. пики (100), (010) и (001) сливаются в один пик. Для сингоний с выделенной осью (тетрагональная, гексагональная, ромбоэдрическая) невозможно определить ориентацию момента в плоскости, перпендикулярной оси. Вывод формул для <M_hkl²> для всех сингоний основан на стандартных формулах геометрической кристаллографии. Например, для кубической сингонии <M_hkl²> = 2/3, т.е., как уже подчеркивалось, не зависит от (hkl). Для ромбической сингонии

<M_hkl²> = 1 - (h²a*²cos²j_a + k²b*²cos²j_b + l²c*²cos²j_c)d², (8.20)

где j_a, j_b, j_c - углы между направлением магнитного момента атома и осями a, b, c, соответственно, a*, b*, c* - параметры обратной ячейки, d =1/H_hkl.

8.5. Анализ магнитной структуры кристалла.

Как правило, определение магнитной структуры кристалла происходит в два этапа. Вначале выделяются дифракционные пики, в интенсивностях которых есть магнитный вклад. По индексам Миллера этих пиков находится волновой вектор магнитной структуры, что зачастую дает возможность установить ее тип. На втором этапе анализируются интенсивности дифракционных пиков для определения собственно магнитной структуры, что включает уточнение величин магнитных моментов S_j и их ориентации относительно осей элементарной ячейки. Факторы заполнения позиций должны быть при этом фиксированы.

Для использования метода Ритвельда необходимо написать параметрическое выражение для интенсивности дифракционного спектра. Поскольку все множители, необходимые для перехода от структурного фактора к интенсивности, являются одинаковыми для ядерного и магнитного вкладов, то:

I(d_i) = C_n 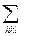j_hkl×L_hkl×(çF_hkl, _nucç² + M_hkl²×çF_hkl, _magç²)×R(d_hkl - d_i) + I_b(d_i), (8.21)

где величина M_hkl² = sin²h для удобства вынесена отдельно, а F_hkl, _mag есть сумма из (8.18).

Поскольку в магнитный структурный фактор входит магнитный форм-фактор P(Q), величина, быстро спадающая с ростом переданного импульса, то магнитный вклад в дифракционный спектр наиболее существенен при малых углах рассеяния, если используется l₀-дифрактометр, или соответственно при больших длинах волн, если эксперимент ведется на TOF-дифрактометре. Для большинства магнитных ионов функции P(Q) определены в независимых экспериментах и занесены в таблицы, которые входят в стандартные программные пакеты.

Для ферромагнитных структур ядерная и магнитная элементарные ячейки совпадают, и магнитное рассеяние дает только какой-то дополнительный вклад в интенсивность дифракционных пиков от атомной структуры. Наоборот, в случае антиферромагнитной структуры как правило возникают дифракционные пики, интенсивность которых определяется только магнитным порядком, т.к. их ядерный структурный фактор равен нулю. Например, возникновение в случае примитивной одноатомной структуры антиферромагнитного порядка заведомо приводит к появлению магнитных дифракционных пиков, соответствующим узлам обратной решетки с полуцелыми индексами (hkl), т.е. там, где ядерные пики отсутствуют.

Пространственная симметрия атомной и магнитной структур может быть различной, т.к. симметрия магнитной структуры определяется только частью атомов. Это означает, что метод анализа данных магнитной дифракции должен допускать использование как элементарных ячеек разного размера, так и разных пространственных групп для описания ядерной и магнитной составляющих дифракционного спектра. Перечисленные особенности анализа магнитных структур поликристаллов в той или иной степени подробности включены в общеупотребительные программные пакеты FullProf и GSAS, а также в MRIA.

Рассмотрим какая информация была получена при анализе магнитных состояний составов LPCM-75, о температурных изменениях кристаллической структуры которых говорилось в разделе 7.2. Измеренные при низкой температуре дифракционные спектры показаны на рис. 8-2. Видно, что в составе с ¹⁸О интенсивными являются пики с полуцелыми индексами, отвечающие AFM структуре. Наоборот, в составе с ¹⁶О существенно выросла интенсивность некоторых пиков, с индексами Миллера основной кристаллической ячейки, хотя пики с полуцелыми индексами также присутствуют в спектре. Таким образом, состав с ¹⁸О находится в чистом AFM состоянии, тогда как состав с ¹⁶О находится в смешанном FM + AFM состоянии. Анализ положений пиков с полуцелыми индексами свидетельствует, что они относятся к AFM структуре типа псевдо-СЕ по классификации, предложенной еще в 1950-х годах (E.O. Wollan & W.C. Koehler, 1955). Эта структура имеет два вектора распространения (0 0 1/2) и (1/2 0 1/2), которые в данном случае отвечают упорядочению магнитных моментов атомов марганца, находящихся в различных узлах ячейки. Из температурной зависимости FM и AFM магнитных моментов (рис. 8-3) в составе с ¹⁶О видно, что при охлаждении образца вначале (при ≈150 К) возникает AFM структура. Средняя величина магнитного момента растет по величине вследствие их постепенного упорядочения. Однако, когда при T ≈ 120 K возникает FM порядок, AFM момент начинает уменьшаться. Эти изменения хорошо интерпретируются в модели фазового расслоения, т.е. возникновения FM кластеров в AFM матрице и последующего их разрастания. Помимо общей картины магнитных превращений анализ нейтронных дифракционных спектров позволил определить величины и направления магнитных моментов атомов Mn.