Интенсивность дифракционных пиков.

В параграфе5.3 было показано, что интегральная интенсивность дифракционного пика, т.е. его площадь или объем, при определенных условиях не зависит от функции разрешения и может быть записана как

I_int = I(k)dk= s(k¢)dk¢, (5.28)

где

s(k) = (8π³/V)·|F_H|²·j(k- 2pH) – (5.29)

дифференциальное сечение когерентного рассеяния нейтронов единичным объемом кристалла в единицу телесного угла. Конкретный вид дельтаобразной функции j(k) связан со степенью совершенства кристалла, линейными размерами кристаллитов и т.д. Вычисление интеграла в (5.28) подробно рассмотрено в книгах [1, 2] (см. также [16, 17]).

Как и в случае дифракции рентгеновских лучей, в кинематическом приближении I_int можно представить в виде произведения трех величин – падающего на кристалл потока нейтронов F, квадрата модуля структурного фактора кристалла |F|² и некоторой функции Q_L (называемой фактором Лоренца), учитывающей геометрический множитель, который зависит от способа сканирования узлов обратной решетки:

I_int(H) = F×V_s×Q_L×|F_H|², (5.30)

где еще учтен объем кристалла V_s. Кроме того, в I_int вводятся поправочные множители, с помощью которых учитываются эффекты поглощения и экстинкции излучения в кристалле. Они рассматриваются в следующих параграфах.

Напомним, что общий вид структурного фактора одинаков для разных типов излучения:

F_H= 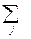b_jexp(2piHr_j)∙exp(-W_j), (5.31)

где H - вектор обратной решетки кристалла, r_j - радиус-вектор j-го атома в элементарной ячейке кристалла, exp(-W_j) - фактор Дебая-Валлера, учитывающий тепловые колебания j-го атома, сумма берется по всем атомам элементарной ячейки. Зависимость структурного фактора от типа излучения определяется величинами b_j: для рентгеновских лучей - это атомные формфакторы, в случае дифракции нейтронов - это когерентные длины рассеяния, которые могут учитывать как ядерное, так и магнитное рассеяние нейтронов.

Для λ₀-дифрактометра F = F₀ – некоторая константа с размерностью [н/см²/с]. Интегрирование по всему узлу обратной решетки с помощью, например, θ-2θ сканирования приводит к следующему выражению для фактора Лоренца:

Q_L(θ) = λ₀³/(V_c²·sin2θ). (5.32)

В результате получаем, что при использовании монохроматического пучка нейтронов интегральная интенсивность дифракционного пика, измеренного в узле H обратной решетки, есть:

I_int(H) = F₀×V_s× λ₀³/(V_c²·sin2θ)×|F_H|², (5.33)

с размерностью [н/с].

Для TOF-дифрактометра F = F'(λ), где F(λ) – функция длины волны, обычно называемая эффективным спектром и имеющая размерность [н/см²/с/Å]. Эффективный спектр формируется из распределения F(λ) (максвелловского) нейтронов по длине волны в первичном пучке, функции η(λ), учитывающей потери в потоке при прохождении пролетных баз от замедлителя до образца и затем до детектора, функции ε(λ), учитывающей эффективность регистрации детектором нейтронов с разными длинами волн. Если первичный пучок формируется зеркальным нейтроноводом, то в η(λ) входит и пропускание нейтроновода.

Интегрирование по узлу обратной решетки в TOF-методе приводит к следующему выражению для фактора Лоренца:

Q_L(λ) = λ⁴/(V_c²·2sin²θ₀), (5.34)

где θ₀ – угол, при котором зарегистрирован дифракционный пик. Можно заметить, что

Q_L(λ) = Q_L(θ)∙(λ/tgθ) = Q_L(θ)∙(dλ/dθ), (5.35)

что соответствует связи между переменными интегрирования dq/tgq = dl/l на λ₀- и TOF-дифрактометрах.

В результате получаем, что интегральная интенсивность дифракционного пика, измеренного в узле H обратной решетки на TOF-дифрактометре, есть:

I_int(H) = F'(λ)×V_s× λ⁴/(V_c²·2sin²θ)×|F_H|², (5.36)

с размерностью [н/с].

Для получения числа отсчетов в обе формулы (5.33) и (5.36) следует еще вставить нормирующую константу, в которую кроме некоторых неучтенных констант, типа телесного угла детектора, входит еще и время измерения дифракционного пика.

5.7. Учет поправок при переходе от интенсивности к структурному фактору.

Формулы (5.33) и (5.36) правильны с точностью до поправок на поглощение и экстинкцию нейтронов в кристалле-образце. С принципиальной точки зрения их учет одинаков для любого типа излучения, но специфика взаимодействия нейтронов с веществом привносит некоторые моменты, требующие рассмотрения. В кинематической теории дифракции поглощение и экстинкцию принято учитывать как независимые факторы, входящие в формулу для интегральной интенсивности. Т.е. для обоих типов дифрактометров вместо I_int(H) следует написать

I'_int(H) = I_int(H)∙A(θ, λ)∙y(θ, λ), (5.37)

где A – фактор поглощения, y – коэффициент экстинкции. Обе поправки зависят от угла Брэгга и длины волны, и должны рассчитываться для конкретных θ и λ, при которых измерен дифракционный пик.

5.7.1. Фактор поглощения. Из элементарного рассмотрения следует, что вероятность уменьшения интенсивности пучка из-за выбывания из него частиц вследствие их поглощения в образце есть А = exp(-ml), где m – линейный коэффициент поглощения, l – пройденный в кристалле путь. Если рассматривать только однократное рассеяние, то для учета всех возможностей достаточно проинтегрировать А по объему образца и разделить на объем, чтобы при m = 0 поправочный фактор превращался в единицу. Итак, фактор поглощения для образца произвольной формы есть:

А = 1/V× exp(-ml)dV, (5.38)

где V – объем образца, l – путь в образце, зависящий от формы образца и от координат точки рассеяния. Для одноэлементного вещества m = n∙s, где n = N/V_c – плотность рассеивающих центров (N – число атомов в ячейке, V_c – объем ячейки), s - сечение взаимодействия, ответственное за выбывание частиц из пучка. Для нейтронов некогерентное выбывание их из пучка возможно из-за поглощения с сечением s_аbs и некогерентного рассеяния с сечением s_inc, т.е. s = s_аbs + s_inc. Сечение некогерентного рассеяния s_inc для всех ядер, кроме водорода, практически не зависит от длины волны. Для водорода из-за его малой массы и, как правило, слабой связи в структуре сечение рассеяния (оно почти полностью некогерентно) изменяется от примерно 20 b для свободного ядра до примерно 80 b для неподвижного ядра (здесь b = 1 барн = 10^-24 см² – единица измерения сечений взаимодействия). Для органических соединений и гидратов используется эмпирическая аппроксимация:

s_{H inc} = (23.2 + 12∙l) b, (5.39)

где l в Å, которая неплохо выполняется в интервале длин волн от 0.7 Å до 3 Å.

Для большинства изотопов сечение поглощения зависит от l в соответствии с формулой (2.5), т.е. s_аbs = s₀(l/l₀). Для изотопов, имеющих резонансы при малых энергиях нейтрона (⁶Li, ¹⁰B, ¹¹³Cd, ¹⁴⁹Sm, ¹⁵⁵Gd, ¹⁵⁷Gd), вследствие чего и сечение рассеяния, и сечение поглощения зависят от длины волны резонансным образом, расчет возможен, если известны параметры резонанса.

Для многоатомного соединения m = ∑ n_j∙s_j, где сумма берется по всем атомам элементарной ячейки или по атомам, входящим в формульную единицу. Во втором случае n_j = k_jZ/V_c, где k_j – число атомов сорта j в формульной единице, Z – число формульных единиц в элементарной ячейке.

5.7.2. Коэффициент экстинкции. Экстинкция, так же как поглощение, приводит к постепенному уменьшению интенсивности пучка по мере его прохождения внутрь кристалла. Различие между ними состоит в том, что если поглощение процесс сугубо некогерентный, т.е. за него несет ответственность конкретный атом, то экстинкция возникает вследствие когерентного взаимодействия падающей волны с кристаллом. В дифракционном эксперименте при некоторых условиях поглощение может отсутствовать совсем, но если есть дифракция, то есть и экстинкция. Для удобства вычислений различают первичнуюивторичную экстинкцию. Под первичной экстинкцией понимают ослабление пучка, происходящее в пределах одного мозаичного блока кристалла. Именно этот процесс является истинно когерентным, т.е. расчет коэффициента первичной экстинкции необходимо вести на уровне амплитуд волн и учитывать фазовые соотношения между ними. Вторичная экстинкция возникает при дополнительном рассеянии уже испытавшей дифракцию волны на каком-то другом мозаичном блоке кристалла. Поскольку волны, испытавшие дифракцию на разных мозаичных блоках, некогерентны (хотя бы потому, что расстояния между блоками произвольны), то расчет можно вести для интенсивностей без какого-либо учета фаз волн. Разработана модель учета экстинкции, базирующаяся на динамической статистической теории рассеяния [N.Kato, 1976], в которой оба процесса рассмотрены совместно и выявлены параметры, от которых зависит реальная ситуация. Оказалось, что в большинстве реальных случаев выполняются критерии, позволяющие проводить учет обоих типов экстинкции с помощью теории переноса излучения, т.е. пренебречь учетом фазовых соотношений.

Существует несколько апробированных алгоритмов учета экстинкции, включенных в пакеты структурных программ. Все они основаны на решении системы дифференциальных уравнений в частных производных, которые в наиболее простом случае выглядят следующим образом:

¶I₀/¶n = -(m_s + m_a)I₀ + m_sI₁, ¶I₁/¶m = -(m_s + m_a)I₁ + m_sI₀, (5.40)

где I₀ и I₁ – интенсивности прямого и рассеянного пучков, nиm – единичные вектора, в направлениях прямого и рассеянного пучков, m_s и m_a – линейные коэффициенты рассеяния (дифракции) и поглощения. Как и ранее m_a должен включать все недифракционные процессы. Структура уравнений (5.40) вполне понятна, видно, что, например, I₀ уменьшается из-за процессов рассеяния и поглощения и увеличивается за счет перерассеяния I₁. Решение этих уравнений с учетом реальной мозаичности и произвольной формы кристалла, а также расходимости первичного пучка, представляет собой сложную математическую задачу и фактически невозможно без упрощающих предположений.

В целом, учет экстинкции в случае дифракции нейтронов не отличается от ее учета при дифракции рентгеновских лучей, и поэтому используются одни и те же алгоритмы (см. соответствующие разделы курса). Следует только заметить, что вследствие меньшего влияния поглощения корректный учет экстинкции при дифракции нейтронов более важен, чем в случае рентгеновских лучей.

5.7.3. Эффективный спектр нейтронов. Рассмотрим еще, как производится учет эффективного спектра нейтронов, необходимый при работе на TOF-дифрактометре.

Если процесс термализации быстрых нейтронов в замедлителе проходит полностью, то вылетающие из него нейтроны распределены по энергии в соответствии с максвелловским распределением (2.1). Его можно перевести в распределение по длине волны для чего надо заменить Е на l и дифференциал dE на dl, вычисленные в соответствии с формулой (2.2):

Ф(l) = 2Ф₀×(l₀⁴/l⁵)×exp(-l₀²/l²), (5.41)

здесь Ф(l) – плотность потока, т.е. поток, приходящийся на единичный интервал длин волн, [Ф(l)] = н/см²/с/Å, Ф₀ – полный поток нейтронов ([Ф₀] = н/см²/с), т.е. Ф₀ = 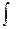Ф(l)dl, l₀ – параметр распределения, связанный с температурой замедлителя соотношением T=949.34/l₀², если Т в градусах Кельвина, а l - в Å.

Реальная форма распределения Ф(l) сильно зависит от параметров замедлителя (толщины, состава) и от того, какие формирующие пучок устройства применяются. Рассмотрим в качестве примера эффекты, возникающие при формировании пучка тепловых и холодных нейтронов с помощью зеркального изогнутого нейтроновода.

Зеркальные нейтроноводы начали широко применяться в нейтронографии после первых удачных экспериментов в конце 1960-х годов. Как правило, эти устройства выполняют двоякую функцию – увеличение потока нейтронов на образце и вывод образца из прямой видимости источника нейтронов для уменьшения фона быстрых нейтронов и γ-квантов. Их принцип действия основан на способности тепловых и холодных нейтронов зеркально отражаться от гладкой плоской поверхности, если угол падения достаточно мал. Для одноатомного материала величина критического угла определяется его когерентной длиной рассеяния и зависит от длины волны нейтрона:

γ_cr = λ(Nb/π)^1/2, (5.42)

где N – число ядер в см³, и для простых металлов, например, никеля, составляет около 6 угловых минут при λ = 1 Å. При углах падения на поверхность γ ≤ γ_cr, коэффициент отражения близок к единице и быстро спадает при γ > γ_cr (рис. 5-14).

Функция пропускания изогнутого нейтроновода с хорошим приближением может быть описана формулами:

Tr(l) = 2/3×k², при k £ 1 и Tr(l) = 2/3×k²[1 – (1 – 1/k²)^3/2], при k ³ 1, (5.43)

где k = l/l* - безразмерный параметр, l* - критическая длина волны нейтроновода, связанная с его радиусом кривизны. На рис. 5-15 показано как изменяется максвелловское распределение после прохождения пучка нейтронов через изогнутый нейтроновод.

Пропускание нейтронов на пролетных базах зависит еще от материала и толщины заглушек нейтроноводов. Его можно представить функцией h(l) = exp(-c₁l-c₂S(l)), где первое слагаемое в показателе экспоненты связано с поглощением, а второе – с рассеянием в материале заглушек, S – сумма когерентного и некогерентного сечений рассеяния. Эффективность детектора, как правило, неплохо аппроксимируется функцией ε(λ) = 1 - exp(-c₃l), c₃ – постоянная.

На практике эффективный спектр нейтронов Ф'(l) определяется экспериментально в стандартной геометрии и с тем же детектором, с которым ведутся основные эксперименты. В этом случае независимого измерения Ф(l), h(l) и ε(λ) не требуются. Наиболее распространенным методом определения Ф'(l) является применение некогерентного рассеивателя, чаще всего ванадия, дифференциальное упругое некогерентное сечение рассеяния которого s_inc в первом приближении рассматривается как изотропное и независящее от длины волны нейтрона. На самом деле у s_inc есть как некоторая зависимость от длины волны, так и легкая анизотропия.

В типичных случаях из функций Ф', А и у наиболее сильно от длины волны зависит именно эффективный спектр нейтронов, изменения которого в рабочем интервале длин волн могут составлять сто и более раз (рис. 5-16). Следует отметить, однако, что вследствие плавного изменения этих величин с длиной волны, возможная некорректность их учета при переходе от интенсивностей к структурным факторам довольно слабо сказывается на определяемых координатах атомов кристалла, хотя значения тепловых параметров атомов могут искажаться значительно.