Дифракция нейтронов на монокристаллах

Наиболее общей задачей, которая может быть решена с помощью дифракции излучения на монокристалле, является восстановление распределения рассеивающей плотности в элементарной ячейке кристалла. Для этого надо измерить интенсивности дифракционных пиков, определить из них структурные факторы и выполнить обратное преобразование Фурье для когерентных длин рассеяния, рассматривая их как непрерывную функцию b(r). Если известна модель структуры, то можно уточнять ее характеристики (параметры элементарной ячейки, координаты атомов, их тепловые факторы, факторы заполнения позиций и т.д.) с помощью какой-либо процедуры минимизации функционала, построенного на разностях измеренных и вычисленных интенсивностей. Для обоих вариантов анализа структуры монокристалла различия между случаями применения рентгеновских лучей или нейтронов не являются принципиальными. Тем не менее, некоторые особенности применения нейтронов имеются, и они рассмотрены далее.

6.1. Структурный анализ монокристаллов.

Напомним основные формулы, необходимые для определения структуры. С учетом поправочных множителей для учета поглощения и экстинкции, формулу (5.30) для интегральной интенсивности дифракционного пика можно записать в следующем виде:

I_int(H) = F×V_s×Q_L×|F_H|²∙A(θ, λ)∙y(θ, λ), (6.1)

где конкретные выражения для потока нейтронов F и фактора Лоренца Q_L зависят от типа дифрактометра. Для l₀-дифрактометра F = const = F₀ – полный поток нейтронов на образце, Q_L = λ₀³/(V_c²·sin2θ). Для TOF-дифрактометра F = F(l) – плотность потока нейтронов на образце, Q_L = λ₀⁴/(2V_c²·sin²θ). Структурный фактор F_H обычно записывается для дискретного набора атомов:

F_H= 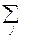b_j∙exp(2piHr_j)∙exp(-W_j), (6.2)

где b_j – когерентная длина рассеяния j-го атома, и является рядом Фурье по отношению к величинам b'_j = b_j∙exp(-W_j). Выполняя обратное преобразование Фурье, получаем:

b(r) = 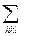F(H_hkl)∙exp(-2piH_hklr), (6.3)

где величина b(r) рассматривается как непрерывная функция в объеме элементарной ячейки, под H_hkl подразумевается дискретный набор векторов обратной решетки кристалла, r – любой вектор в элементарной ячейке. Анализ вида функции b(r) – величины и координат ее максимумов – позволяет определить тип и координаты атомов структуры.

Как видно из приведенных формул, задача анализа структуры кристалла в нейтронографии может быть решена стандартным образом. Специфической особенностью, возникающей на этом этапе, является отсутствие положительной определенности b(r), имеющейся при анализе дифракции рентгеновских лучей. В отдельных случаях это обстоятельство может затруднить анализ, однако именно эта особенность дает возможность провести детальное рассмотрение распределения в ячейке ядерной плотности атомов водорода, т.к. когерентная длина рассеяния водорода отрицательна и резко контрастирует с плотностью распределения других атомов.

Еще одна специфическая особенность использования формулы (6.3) в нейтронографии состоит в способах определения фаз структурных факторов. Они рассматриваются в следующем параграфе.

Другим стандартным методом решения структурной задачи является описание ее с помощью набора параметров и определение или уточнение этих параметров с помощью минимизации функционала:

c² = 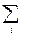w_i(J_i - I_i)², (6.4)

где w_i – вес i-й точки, J_i и I_i - измеренные и вычисленные интегральные интенсивности дифракционных пиков. Параметрами могут быть координаты атомов, их тепловые факторы, некоторые величины, входящие в выражения для экстинкции и т.д.

6.2. Определение фаз структурных факторов.

Нейтронные структурные факторы, так же как рентгеновские, являются в общем случае комплексными величинами, т.е. F(H) = F_r(H) + iF_im(H) = |F(H)|·e^iφ(H), и для выполнения суммирования в формуле (6.3) необходимо знать их вещественную и мнимую части или их модули и фазы. Модули структурных факторов определяются непосредственно из (6.1) после введения всех необходимых поправочных множителей. Наоборот, поскольку прямая информация о фазах структурных факторов в измеряемых интенсивностях дифракционных пиков отсутствует, задача их определения является одной из наиболее сложных в структурном анализе кристаллов. Более того, в случае рассеяния нейтронов она становится более сложной, чем при использовании рентгеновских лучей.

В рентгеноструктурном анализе сформировались несколько весьма эффективных методов определения величин φ(H). Их можно разделить на прямые (или статистические) методы, которые основаны на анализе соотношений между измеренными интенсивностями, и специальные, к которым относятся методы тяжелого атома, изоморфных замещений и аномального рассеяния. Практика структурной нейтронографии показала, что для нее фактически ни один из перечисленных методов не является эффективным. Прямые методы во многом основаны на факте положительной определенности электронной плотности в элементарной ячейке, тогда как в практически интересных для использования нейтронов случаях (водородсодержащие структуры) часть атомов имеет положительную, а часть – отрицательную когерентную длину рассеяния. Понятие тяжелого атома в нейтронографии отсутствует, т.к. подавляющее большинство элементов и изотопов имеют соизмеримые по величине длины рассеяния.

Единственным методом, прошедшим в нейтронном структурном анализе практическую проверку, оказался метод аномального рассеяния. Он основан на явлении резонансного ядерного рассеяния, рассмотренного в параграфе (2.2.1), в соответствии с которым амплитуда (или длина) рассеяния какого-либо атома резонансным образом зависит от энергии нейтрона (формула (2.3)). Для использования этого эффекта в нейтронографии наиболее подходящими являются изотопы ¹¹³Cd, ¹⁴⁹Sm и ¹⁵⁷Gd, имеющие резонансы в интервале длин волн от 0.68 Å (¹¹³Cd) до 1.61 Å (¹⁵⁷Gd). Для определения фазы структурного фактора необходимо измерить интенсивность соответствующего дифракционного пика при двух или нескольких длинах волн. Успех применения метода зависит от того, насколько велики разности интенсивностей (разности Бейвута) инверсных пиков, т.е. I(H) и I(-H). Можно показать, что они определяются отношением f_i/f₀, где f₀ – амплитуда потенциального рассеяния (первое слагаемое в (2.3)), f_i – мнимая часть амплитуды рассеяния (второе слагаемое в (2.3) при E = E₀). При использовании аномального рассеяния рентгеновских лучей это отношение обычно не превышает 0.1 – 0.2. В случае рассеяния нейтронов, для перечисленных изотопов, оно намного больше, от 6.8 (¹¹³Cd) до 8.8 (¹⁵⁷Gd), что позволяет ограничиться сравнительно малой концентрацией резонансно рассеивающих ядер в структуре. Оценки показывают, что, например, использование изотопа ¹¹³Cd может привести к успеху при его содержании в структуре на уровне 1/2000 (A.K.Singh & S.Ramaseshan, Acta Cryst. B24 (1968) 35).

Идея “управления” величиной амплитуды рассеяния отдельных атомов структуры для определения фаз структурных факторов в случае рассеяния нейтронов может быть реализована еще и с использованием их магнитного взаимодействия (Ф.Л.Шапиро, 1970). Для этого необходимо присутствие в молекуле одного или нескольких парамагнитных атомов и измерение интенсивностей дифракционных пиков при наложении на кристалл внешнего магнитного поля с разной величиной и направлением.

Следует признать, однако, что эти предложения и попытки их реализации были сделаны достаточно давно, когда проблема определения фаз в рентгеновском структурном эксперименте была сравнительно острой. За прошедшее время ситуация изменилась кардинально и стандартным подходом сейчас является определение модели структуры в рентгеновском эксперименте, расчет по ней фаз нейтронных структурных факторов и их последующее уточнение с учетом всех атомов структуры, в том числе, атомов водорода.

6.3. Непрерывное сканирование обратного пространства.

В параграфе 5.2 было показано, как можно реализовать непрерывное сканирование больших площадей или объемов обратного пространства. Особенно эффективно это может быть организовано на TOF-дифрактометре при использовании 2D детектора. Величина наблюдаемого объема зависит от телесного угла детектора, Ω_det, и ограничений на минимальное и максимальное значения волновых векторов. Последнее связано с уменьшением потока нейтронов при малых и больших длинах волн. Если средний угол Брэгга, θ₀, не мал, то наблюдаемый в обратном пространстве объем есть:

V* = 2/3·(1/λ³_min – 1/λ³_max)·sin²θ₀·Ω_det, (6.5)

где λ_min, λ_max – границы рабочего интервала спектра нейтронов. Число узлов обратной решетки, содержащихся в V*, слабо зависит от ориентации кристалла и составляет N ≈ V*·V_c, где V_c – объем элементарной ячейки. Для λ_min = 1 Å, λ_max >> λ_min, θ₀ = 45° и Ω_det = 0.1 ср получаем V* ≈ 0.03 Å^-3, и для кристалла с V_c = 500 ų одновременно будут наблюдаться около 15 дифракционных пиков. Для кристаллов белков, объем элементарной ячейки которых составляет более 10⁴ ų, число одновременно наблюдаемых узлов обратной решетки составляет несколько сотен, что, естественно, позволяет резко ускорить эксперимент. Следует особо подчеркнуть, что измерение интегральных интенсивностей в наблюдаемом объеме происходит при этом без каких-либо поворотов кристалла или детектора.

Необходимость непрерывного сканирования обратного пространства возникает и во многих других дифракционных задачах, решаемых на монокристаллах. Прежде всего, можно назвать изучение трансформационного двойникования кристалла, несоизмеримо модулированных структур, спиралевидных магнитных структур, диффузного рассеяния.

Трансформационное двойникование наблюдается в кристаллах ферроэластиков при их переходе в низкосимметричную фазу, который в общем случае можно описать как образование составной обратной решетки кристалла. В дифракционном эксперименте это проявляется как расщепление одиночных пиков высокосимметричной фазы на несколько компонент (рис. 6-1). Определение характеристик компонент позволяет получить количественную информацию о геометрических параметрах двойников (доменов), а также об изменениях доменной структуры под действием внешних полей. Найденные из эксперимента положения компонент могут быть связаны с координатами точек в обратном пространстве, т.е. могут быть определены угол спонтанного сдвига, линейная деформация решетки и т.д.

Например, характеристики доменной структуры кристаллов KD₂PO₄ (DKDP), которые при температуре около 214 К испытывают фазовый переход из тетрагональной фазы в ромбическую, были исследованы на TOF-дифрактометре с применением 1D детектора. В соответствии со схемой образования составной обратной решетки при переходе из тетрагональной в ромбическую фазу рефлексы типа [h00] расщепляются на три, а любые другие рефлексы - на четыре компоненты, и измеренное распределение интенсивности в окрестности узла (220), показанное на рис. 6-1, подтверждает это предположение. По величине расщепления легко может быть рассчитан угол спонтанного сдвига (для DKDP он оказался равен 31.3 угл. мин.) или изменения параметров ячейки при переходе, а интенсивность отдельных компонент узла характеризует относительное количество доменов с той или иной ориентацией.

Несоизмеримо (или несоразмерно) модулированная структура в кристаллах часто возникает как промежуточное состояние при структурном переходе в менее симметричную фазу, например, при переходе из пара- в сегнетофазу в сегнетоэлектриках. Другим распространенным случаем являются несоизмеримая модуляция магнитной структуры. В обоих случаях имеется в виду, что наряду с обычной трехмерной периодичностью кристаллической структуры на положение какого-то одного или группы атомов, или величины и направления магнитного момента наложена дополнительная модуляция, период которой несоизмерим с основными трансляциями. Можно показать (конкретный пример приведен в параграфе 8.3), что при этом в дифракционном спектре возникают дополнительные пики (сателлиты), положения которых в обратном пространстве можно представить вектором H_hklm = H_hkl + mq_δ, где H_hkl – вектор узла обратной решетки кристалла с индексами Миллера (h k l), m – целое число, q_δ – вектор модуляции. Несоизмеримость модуляции проявляется в том, что ее период Т_δ, который пропорционален 1/|q_δ|, не связан рациональным отношением с периодами элементарной ячейки кристалла.

Вектор q_δ может быть разложен по базису (a*b*c*) – векторов основных трансляций в обратной решетке и это разложение определяет характер модуляции: вдоль какого-то одного направления, в сечении или в объеме кристалла. На рис. 6-2 показано как выглядит дифракционная картина, измеренная на монокристалле Sr_xBa_1-xNb₂O₆ (SBN) с x = 0.7, модуляция структуры которого приводит к появлению сателлитов с q_δ = 0.305(±a* ± b*) + c*/2. Эксперимент был проведен на TOF-дифрактометре при использовании 1D детектора, охватывавшего сектор Δθ = ±2.5° по углу Брэгга. Модуляция структуры кристалла связана с искажениями кислородных октаэдров, причем вследствие ее несинусоидального характера наблюдаются сателлиты 2-го порядка, т.е. с m = 2, интенсивность которых сравнительно мала. Довольно очевидно, что наблюдение столь сложных распределений интенсивности возможно только при непрерывном сканировании обратного пространства.

Еще одним примером использования TOF-дифрактометра для двумерного сканирования обратной решетки является изучение теплового диффузного рассеяния нейтронов в кристаллах. На рис. 6-3 показана окрестность узла (002) в кристаллах SBN в виде объемной картинки и контуров равной интенсивности. Наблюдаемые крылья интенсивности связаны с рассеянием нейтронов на длинноволновых акустических фононах и хорошо описываются имеющимися моделями (B.T.M.Willis, 1986). Их анализ позволяет, в частности, оценить скорость распространения звука в кристалле вдоль конкретного направления.

6.4. Совместный анализ данных рентгеновского и нейтронного экспериментов.

Построение распределения рассеивающей плотности по нейтронным данным дает информацию о положении ядра атома, тогда как обработка рентгеновских данных позволяет выявить распределение электрического заряда вокруг ядра. Соответственно, совместный анализ рентгеновских и нейтронных дифракционных данных иногда позволяет получить важную дополнительную информацию о деталях электронной структуры кристаллов.

Основная идея метода основана на том, что по нейтронным данным можно с хорошей точностью фиксировать положение ядра и, следовательно, сферически симметричной части распределения электронов. В принципе, выделение сферически симметричной части электронного облака только по рентгеновским данным также возможно, но в сложных случаях достижению необходимой точности мешает сильная корреляция позиционных и тепловых параметров, а также недостаточная точность в задании рентгеновских форм-факторов. Особенно сильно это проявляется в случае структуры, содержащей легкие атомы, такие как водород или кислород.

Технически задача сводится к выполнению рентгеновского и нейтронного эксперимента на монокристалле, уточнению структуры по нейтронным данным и построению, так называемых, X – N фурье-синтезов:

Δb(r) = 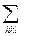[F_x(H_hkl) - F_c(H_hkl)]∙exp(-2piH_hklr), (6.6)

где Δb(r) называется разностной (или деформационной) плотностью, F_x – экспериментальные рентгеновские структурные факторы, F_c – рентгеновские структурные факторы, рассчитанные с использованием нейтронных данных, т.е. по координатам атомов и тепловым параметрам, определенным в нейтронном эксперименте.

Расчет F_c в зависимости от типа задачи ведется по той или иной модели, в которую, например, закладываются сферические атомные форм-факторы. В результате Δb(r) будет содержать информацию о различиях рентгеновских и нейтронных координат центров распределений и об отклонениях распределения электронной плотности от модели, например, от сферической симметрии. Большой фактический материал по совместному использованию рентгеновских и нейтронных дифракционных данных для анализа ковалентных связей приведен в книге [2, 1-й том].