Геометрические характеристики дифракционных пиков.

В ходе дифракционного эксперимента на кристалле измеряются дифракционные пики, характеристики которых связаны со структурными параметрами кристалла. Из набора положений пиков могут быть определены параметры элементарной ячейки кристалла. Из интенсивностей пиков может быть извлечена информация о структурных факторах кристалла, из которых далее определяются координаты атомов. Ширины дифракционных пиков связаны с параметрами, характеризующими микроструктуру кристалла – размер кристаллитов, мозаичность, уровень микронапряжений. Таким образом, первый этап дифракционного эксперимента предполагает определение основных геометрических характеристик дифракционных пиков, к которым относятся его положение, площадь (или объем в случае 3D сканирования) иширина.

Для их корректного определения необходимо измерить зависимость интенсивности дифракционного пика от вектора рассеяния, т.е. в общем случае трехмерную функцию I(k). Эта зависимость (или форма дифракционного пика) определяется, по крайней мере, двумя обстоятельствами. Во-первых, узлы обратной решетки имеют собственную форму, связанную с микроструктурой кристалла. Во-вторых, в измеряемую форму дифракционных пиков вносит вклад функция разрешения дифрактометра. Можно показать, что измеряемая в эксперименте зависимость I(k) является сверткой функции разрешения R(k) и сечения когерентного рассеяния s(k):

I(k) = R(k¢-k)·s(k¢)dk¢, (5.3)

где формально предполагаются бесконечные пределы интегрирования.

Основные сведения о функции разрешения дифрактометра и о свойствах свертки функций приведены далее в разделе 5.5.

Если размеры когерентных областей велики, а мозаичность кристалла мала, то s(k) ~ d(k-2pH) и форма пиков полностью определяется функцией R. Наоборот, при узкой функции разрешения и не очень больших размерах рассеивающих когерентных областей можно изучать их форму.

Зная I(k) можно формально определить положение пика как его центр тяжести

P= kI(k)dk/ I(k)dk, (5.4)

где P – вектор в k-пространстве, который нетрудно выразить в экспериментальных координатах (2q или t) или перевести в H-пространство. Иногда предпочитают определять положение пика как максимум распределения I(k). Очевидно, что для симметричных пиков оба определения дают одинаковый результат.

Ширина пика естественным образом определяется через его дисперсию, которая по определению есть

D= (k - P)²I(k)dk/ I(k)dk, (5.5)

причем D задает некоторую поверхность в k-пространстве, например, трехмерный эллипсоид, оси которого могут иметь разную длину и быть произвольно ориентированными.

Площадь (или объем) пика есть просто интеграл

S = I(k)dk= 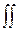R(k¢-k)s(k¢)dk¢dk = s(k¢)dk¢~ |F_H|², (5.6)

т.к. предполагается, что интеграл R(k¢-k)dk нормирован на единицу. Эта величина (ее обычно называют интегральной интенсивностью) не зависит от, как правило, неизвестной функции разрешения, если, конечно, интегрирование по kи k¢выполнено в достаточно широких пределах. Следовательно, находя интегральные интенсивности можно определить модули структурных факторов. Коэффициент пропорциональности между S и |F_H|² в (5.6) зависит от H и от метода сканирования узлов обратной решетки. Эти зависимости рассмотрены в разделе 5.6.

5.4. Основные параметры нейтронного дифрактометра.

Как уже упоминалось, постепенное развитие нейтронографии привело к появлению очень разных по сути задач, требующих, соответственно, различного подхода. Например, цель и постановка структурного эксперимента на монокристалле радикально другие, чем в эксперименте по определению внутренних напряжений в объемном изделии. Еще одним фактором, оказывающим решающее влияние на организацию нейтронного эксперимента, является относительная слабость потока нейтронов даже от современных мощных источников, по сравнению с потоками γ-квантов от рентгеновской трубки и, тем более, от источника синхротронного излучения. Как следствие, нейтронные дифрактометры приходится оптимизировать по какому-то параметру, т.е. делать их специализированными.

Основными параметрами дифрактометра, подлежащими оптимизации, являются его светосила и разрешающая способность, которые, как правило, находятся в антагонистическом соотношении, т.е. улучшение светосилы ухудшает разрешение и наоборот. В некоторых случаях важным параметром оказывается доступный диапазон переданных импульсов. Обсудим эти параметры на примере нейтронного TOF-дифрактометра для поликристаллов.

Под светосилой дифрактометра удобно понимать величину

J₀= F₀×S×W_d/4p, (5.7)

где F₀ – поток нейтронов на образце ([F₀] = н/см²/с), S – доступная площадь образца ([S] = см²), W_d/4p – доля телесного угла, охватываемого детектором. Соответственно размерность светосилы есть [J₀] = н/с. Зная светосилу, можно оценить время эксперимента, необходимое для получения статистически значимого результата. Поток нейтронов на современных дифрактометрах составляет ~5·10⁶ н/см²/с, телесный угол детекторной системы может быть доведен до ~1 ср. При площади образца 2 см² светосила достигает ≈10⁶ н/с. При полной рассеивающей способности образца d ≈ 0.1 (доли нейтронов, рассеянных в 4p стерадиан, от полного количества падающих на образец) получаем, что полная скорость счета может составить 10⁵ н/с. Это достаточно большая величина, вполне обеспечивающая измерение спектра за время t_s ≈ 1 час или даже в течение нескольких минут. Конкретные значения величин в (5.7) зависят от источника нейтронов, конструкции дифрактометра, детекторной системы и оптимизации дифрактометра по тому или иному параметру.

Под разрешающей способностью (разрешением) дифрактометра для поликристаллов принято понимать относительную ширину дифракционного пика, т.е. величину R(d₀) = (Δd/d₀), где Δd – полная ширина пика, измеренного при d = d₀, на половине его высоты. Зная разрешение можно оценить степень различимости дифракционных пиков, имеющих близкие d_hkl. Во избежание путаницы, подчеркнем еще раз, что в соответствии с формулой (5.3) функция разрешения определяет форму дифракционных пиков, тогда как разрешающая способность (или разрешение) есть относительная ширина этой функции. Часто зависимость разрешения от какой-либо переменной также называют функцией разрешения и обозначают той же буквой R. Однако из контекста обычно ясно, что имеется в виду – форма пика или зависимость его ширины от, например, угла рассеяния. Из формулы Вульфа-Брэгга следует, что в первом приближении относительную ширину пика можно представить в следующем виде:

R(d₀) = (Δd/d₀) = [(Δλ/λ₀)² + (Δθ/tgθ₀)²]^1/2, (5.8)

где Δλ/λ₀ – величина, характеризующая степень монохроматизации первичного пучка, θ₀ – угол Брэгга, при котором измерен дифракционный пик, Δθ – характеризует разброс в угле Брэгга, связанный с геометрическими неопределенностями процесса рассеяния и является полной шириной на половине высоты соответствующей функции распределения. Разброс в угле Брэгга зависит от коллимации первичного пучка, размеров образца и угловых размеров детектирующего элемента. Из формул (5.7) и (5.8) видно, в чем может заключаться противоречие в попытке одновременного увеличения светосилы и улучшения разрешения – уменьшение Δλ и Δθ улучшает разрешение, но поток нейтронов на образце при этом будет уменьшаться.

Диапазон измеряемых межплоскостных расстояний не коррелирует напрямую с разрешением и светосилой, а в основном определяется конструкцией дифрактометра. Например, в случае l₀-дифрактометра диапазон углов рассеяния обычно ограничен значениями 2θ = (10° - 170°), a рабочая длина волны выбирается вблизи максимума максвелловского распределения, т.е. l₀ = (1 – 2) Å. Из уравнения Вульфа-Брэгга следует, что диапазон d_hkl составит (0.5 – 11) Å. Продвижение в сторону меньших или больших d_hkl возможно при использовании нейтронов от “горячего” или “холодного” замедлителя, соответственно.

5.5. Разрешающая способность нейтронных дифрактометров.

Разрешающая способность нейтронного дифрактометра является одной из его наиболее важных характеристик и поэтому требует специального рассмотрения. Ее величина и функциональная зависимость от вектора рассеяния во многом определяют возможность решения той или иной дифракционной задачи. В некотором смысле, разрешение является более важным параметром дифрактометра, чем светосила, т.к. при недостаточном разрешении ничто не поможет увидеть раздельно близкорасположенные пики, тогда как недостаток светосилы зачастую можно компенсировать бóльшим временем измерения спектра.

5.5.1. Общее рассмотрение. Функция разрешения R(k₀,k) определяет вероятность измерения на дифрактометре события, относящегося к точке k обратного пространства, если дифрактометр настроен на измерение в точке k₀. В идеальном случае, т.е. если размеры источника, образца и детектора малы, а разброс по длине волны отсутствует или мал (Δλ ≈ 0), то R(k₀,k) ≈ δ(k-k₀). Если эти условия не выполняются, то каждой из переменных, характеризующих процесс дифракции, можно сопоставить некоторую функцию распределения. Например, для расчета функции разрешения необходимо задать распределения нейтронов по углам падения на образец, P₁(γ₁), и по отклонению от среднего угла рассеяния при регистрации рассеянного пучка детектором, P₂(γ₂), которые в простейшем случае являются прямоугольными распределениями типа P(γ) = 1/2γ₀, если |γ| ≤ γ₀ и G(γ) = 0 при |γ| > γ₀. Результирующая функция, дающая вероятность появления того или иного значения угла рассеяния, является сверткой P₁ и P₂. Рассматривая аналогичным образом все источники неопределенностей, т.е. возможных отклонений переменных от их средних значений в процессе дифракции, можно найти функцию разрешения R(k₀,k). Это непростая задача, т.к. для некоторых переменных необходимо учитывать их связь друг с другом как, например, для длины волны и угла Брэгга (конкретный пример расчета приведен в следующем параграфе). Кроме того, реальные распределения, как правило, являются функциями, с которыми неудобно проводить вычисления. Задача существенно упрощается, если воспользоваться гауссовым приближением при задании распределений вероятностей. В наиболее общем виде такого рода вычисления были выполнены в работах румынских физиков (A.Stoica, M.Popovici, 1975), которыми было показано, что в гауссовом приближении трехмерная функция разрешения может быть записана в виде:

R(X) = (2π)^-3/2·||М_ij||·exp(-1/2·M_ijX_iX_j), (5.9)

где X = k-k₀, М_ij – некоторая матрица, по повторяющимся индексам i и j предполагается суммирование от 1 до 3, двойными вертикальными скобками обозначен детерминант матрицы, функция R(X) нормирована на единицу. Можно показать, что матрица М_ij является обратной к матрице (S = M^-1), которая представляет собой матрицу вторых моментов <X_iX_j>, а детерминант ||М_ij|| определяет объем разрешения в обратном пространстве. Для вычисления матрицы S необходимо задать функции распределения первичных переменных, типа P₁(γ₁) и P₂(γ₂) и аппроксимировать их гауссианами. В этом случае прямоугольные распределения заменятся на эллипсы. Подробное изложение этого метода расчета функции разрешения содержится в книге [14]. Было показaно, что замена реального распределения на гауссиан с одинаковой дисперсией дает хорошее соответствие с точным расчетом, если исходные распределения более-менее симметричны (т.е. третий момент близок нулю) и таких распределений, по крайней мере, несколько. Некоторые проблемы возникают для TOF-дифрактометра в том случае, когда нейтронный импульс имеет явно выраженную асимметрию, как это бывает на источниках типа SPS.

5.5.2. TOF-дифрактометр для монокристаллов. В экспериментах с монокристаллами больший интерес представляет не сама функция разрешения, а профиль дифракционного пика, который помимо дифрактометра зависит еще и от микроструктуры образца. Приведем в качестве примера расчет профиля дифракционного пика от монокристалла, измеряемого на TOF-дифрактометре, с учетом его мозаичности, предполагая для упрощения, что размер монокристалла мал.

Схема эксперимента представлена на рис. 5-9. Для не очень больших углов рассеяния (tgq₀ << 2/f², где f - вертикальная расходимость нейтронного пучка) достаточно рассмотреть проекцию нейтронных путей на горизонтальную плоскость и учесть следующие распределения: P(g₁) - плотность вероятности попадания нейтрона на образец под углом g₁ к направлению k₁₀, W(g₂)- плотность числа мозаичных блоков, ориентированных под углом g₂ к среднему направлению H₀ и Z(e) - форму импульса нейтронов, вылетающих из замедлителя. Вектора k₁₀ и k₂₀ на рис. 5-9 обозначают средние направления от источника на образец и от образца на детектор. Переменные g₁ и g₂ связаны друг с другом через условия:

k∙sinq = pH, k₂ - k₁ = 2pH, k₁ = k₂. (5.10)

Плотность вероятности регистрации детектором нейтрона с волновым вектором k₂ eсть G_s ~ P(g₁)×W(g₂), причем из (5.10) с учетом малости углов g₁ и g₂ следует:

g₁ + g = 2g₂, g₁ - g = 2xtgq₀, (5.11)

где g угол между векторами k₂₀ и k₂, x = (k - k₀)/k₀ - относительное отклонение модуля k от его среднего значения k₀ = k₁₀ = k₂₀. Разрешая систему (5.11) относительно g₁ и g₂, для G_s получаем:

G_s(g,x) ~ P(g + 2xtgq₀)×W(g+xtgq₀). (5.12)

Учет вкладов в (5.12) от случайных переменных, некоррелирующих с x и g, проводится вычислением соответствующих сверток. Например, Z(e) учитывается переходом от G_s к

G¢_s(g,x) ~ G_s(g,x-e)Z(e)de. (5.13)

Функция G¢_s(g,x) описывает форму двумерных дифракционных пиков и для монокристалла с малой мозаичностью совпадает с проекцией функции разрешения дифрактометра R(k₀,k) на плоскость рассеяния.

Если вместо точного задания плотности вероятности тех или иных распределений воспользоваться их аппроксимацией гауссианами с соответствующими дисперсиями, то двумерное распределение G¢_s(g,x) будет эллипсом, некоторым образом повернутым относительно осей координат g и x. В этом случае легко получить дисперсии по переменным g и x как для полного распределения G¢_s(g,x), так и для его проекций на оси g и x:

D_g = g₀² + 4h², D_x = D_t + (g₀² + h²)/tgq₀, (5.14)

где g₀², h² и D_t, - дисперсии распределений P(g₁), W(g₂) и Z(e), соответственно.

5.5.3. l₀-дифрактометр для поликристаллов.Разрешение l₀-дифрактометра принято записывать в следующем виде:

R(d₀) = 1/2·D2q/tgq, (5.15)

где D2q – полная ширина профиля дифракционного пика, измеренного как функция угла рассеяния 2q. Предполагая стандартную геометрию дифрактометра для поликристаллов (рис. 5-10): коллиматор с параметром α₁ (угол расходимости) перед монохроматором, монохроматор (имеющий мозаичность β) с углом Брэгга θ_М, коллиматор с параметром α₂ перед образцом, коллиматор с параметром α₃ перед детектором, стоящем на угле рассеяния 2q, ширину пика можно записать как (G.Cagliotti, A.Paoletti, F.P.Ricci, 1958):

D2q = (U·tg²q + V·tgq + W)^1/2. (5.16)

В этой формуле величины U, V и W являются параметрами, которые могут быть измерены в эксперименте с модельным образцом, но могут быть и рассчитаны по следующим формулам:

U = 4(α₁²α₂² + α₁²β² + α₂²β²)/tg²θ_М∙(α₁² + α₂² + 4β²), (5.17)

V = - 4α₂²∙(α₁² + 2β²)/tgθ_М∙(α₁² + α₂² + 4β²), (5.18)

W = [α₁²α₂² + α₁²α₃² + α₂²α₃² + 4β²(α₂² + α₃²)]/(α₁² + α₂² + 4β²). (5.19)

Анализ этих формул показывает, что при некоторых соотношениях между величинами можно достичь оптимального соотношения между интенсивностью и шириной дифракционных пиков в определенной области углов рассеяния. Часто выбирают следующее соотношение a₂ = 2β > a₁ ≈ a₃, тогда

U ≈ (2.5α₁² + 2β²)/tg²θ_М, (5.20)

V ≈ - (2α₁² + 4β²)/tgθ_М, (5.21)

W ≈ 0.5α₁² + 2β² + α₃². (5.22)

Типичные кривые, рассчитанные с применением этих формул, показаны на рис. 5-11.

5.5.4. TOF-дифрактометр для поликристаллов. В случае анализа поликристаллического вещества форма пика определяется одномерной функцией и разрешение принято выражать в виде R(d) = Dd/d, где d - межплоскостное расстояние. Как правило, для расчета R(d) достаточно учесть три слагаемых:

R(d) = [(Dt₀/t)² + (Dq/tgq)² + (DL/L)²]^1/2, (5.23)

где t - полное время пролета от источника до детектора, q - угол Брэгга, L – полное пролетное расстояние от источника до детектора, Dt₀ – ширина нейтронного импульса от источника, Dq включает все угловые неопределенности процесса рассеяния, DL учитывает неопределенность пролетного расстояния. Как обычно, D означает полную ширину на половине высоты соответствующей функции распределения. Например, если распределение по времени вылета нейтронов из замедлителя представлено в виде гауссовой функции

Z(e) = (sÖ2p)^-1exp(-e²/2s²), (5.24)

где s = D_t^1/2 - среднеквадратичное отклонение, то Dt₀ = 2(2ln2)^1/2s » 2.355s.

Первое слагаемое в (5.23) (обозначим его R_t) можно записать как

R_t = Dt₀/t = Dt₀/(252.778 Ll) = Dt₀/(505.556 Ldsinq), (5.25)

где величины Dt₀, L и l или d выражается в мкс, м и Å соответственно. На импульсных источниках типа SNS с коротким импульсом быстрых нейтронов величина Dt₀ в основном определяется конструкцией замедлителя и при больших длинах волн она пропорциональна l, а именно Dt₀ » 15l (в мкс, если l в Å). В этом случае R_t не зависит от d, определяется только полным пролетным расстоянием и уже при L = 30 м может быть достигнут уровень R_t = 0.002, что является характерным значением для дифрактометра высокого разрешения. Наоборот, на импульсных источниках с длинным импульсом Dt₀ слабо зависит от l, т.е. в первом приближении Dt₀ = const, и R_t ~ 1/d.

В угловую часть функции разрешения R_q = Dq/tgq в основном вносят вклад величина коллимации первичного пучка нейтронов, размеры образца и детектора. При рассеянии назад, т.е. при углах близких к 180°, величина R_q может быть сделана весьма малой. При малых линейных размерах замедлителя, образца и детектора величина DL, как правило, очень мала по сравнению с полным расстоянием и соответственно вклад третьего слагаемого в (5.23) мал. На рис. 5-12 показано как ведет себя ширина функции разрешения TOF-дифрактометра на источнике типа SPS при пролетной базе около 100 м и детекторе на большом угле рассеяния.

Для TOF-дифрактометров разработан прием, позволяющий увеличить светосилу дифрактометра при сохранении или даже улучшении разрешающей способности, называемый фокусировкой по времени. Ее суть состоит в том, что при дифракции, т.е. при выполнении условия Вульфа-Брэгга, есть полная корреляция между углом рассеяния и длиной волны (скоростью) нейтрона, и полное время пролета нейтрона может быть сделано постоянным для нейтронов с разной длиной волны, если они пролетают разные пути. Например, для замедлителя и детектора, имеющих вид пластин (рис. 5-13), при соблюдении следующих условий

2(L₁/L)×tga₁tgq₀ = 1, 2(L₂/L)×tga₂tgq₀ = 1, (5.26)

где a₁ и a₂ – углы наклона замедлителя и детектора к среднему пути, L₁ и L₂ – расстояния от замедлителя до образца и от образца до детектора, оказывается, что в первом приближении слагаемое R_q равно нулю.

Метод временной фокусировки для TOF-дифрактометров был независимо и почти одновременно предложен Дж.Карпентером в США и А.Холасом в Дубне и впервые реализован на реакторе ИБР. В экспериментах с поликристаллами этот метод позволяет существенно (в ~5 раз) увеличить светосилу дифрактометра без заметного ухудшения разрешающей способности и до настоящего времени продолжает широко использоваться. Если применяется детектор больших размеров, то линейные условия (5.26) становятся слишком грубым приближением и фокусирующая линия или поверхность находятся из решения дифференциального уравнения dL/L + dq/tgq = 0.

С появлением позиционно-чувствительных детекторов с хорошим пространственным разрешением и многоэлементных детекторных систем начала применяться временная “электронная фокусировка”, состоящая в независимой регистрации дифракционных спектров отдельными детекторными элементами с последующим суммированием отсчетов с необходимым сдвигом по временной координате.

Фокусировка по времени не затрагивает R_t. Для уменьшения этой части полной функции разрешения существуют два пути, которые очевидны из выражения (5.25) – сокращение Dt₀ или увеличение пролетного расстояния. Оба эти фактора могут быть использованы при создании TOF-дифрактометров на источниках с узким импульсом. Например, малая ширина импульса быстрых нейтронов на источнике ISIS (Великобритания) и специальная конструкция замедлителя позволили иметь ширину импульса тепловых нейтронов около 15 мкс/Å, что при увеличении L до ~100 м дало возможность довести R_t до 0.0006. Нейтронный дифрактометр с таким высоким разрешением по межплоскостному расстоянию уступает лишь незначительно лучшим установкам на современных синхротронных источниках. К сожалению, при этом значительно теряется светосила, во-первых, из-за неполного замедления нейтронов в тонком замедлителе и, во-вторых, из-за необходимости устранения нескольких импульсов источника для предотвращения рецикличности нейтронов на большом пролетном расстоянии.

5.5.5. Нейтронный фурье-дифрактометр. Расчет функции разрешения в этом случае ведется так же, как и для TOF-дифрактометра, т.е. по формуле (5.23). Можно показать, что для временной части функции разрешения справедливо выражение

R(t) » W^-1 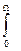g(n)cos(2πnt)dn, (5.27)

где g(n) - функция распределения частот вращения прерывателя, а W - максимальная частота модуляции потока нейтронов фурье-прерывателем. Если максимальная частота вращения прерывателя есть n_max, а число щелей на прерывателе – N, то W = N∙n_max. Ширина R(t) в основном определяется значением W, а именно Dt₀ » 1/W, которую и следует подставлять в (5.23). При частоте вращения прерывателя 150 Гц и числе щелей на роторе 1024 (параметры фурье-прерывателя, действующего на ИБР-2) получаем, что W » 150 кГц и Dt₀ » 7 мкс. В этом случае временная компонента функции разрешения при L = 20 м, для d = 2 Å составит 0.00035, что почти в 2 раза лучше, чем для обычного TOF-дифрактометра на 100 м пролетной базе на источнике типа ISIS. В оптимальном варианте детекторная система фурье-дифрактометра конструируется таким образом, чтобы временная и угловая относительные дисперсии (1-е и 2-е слагаемые в 5.23) были одинаковы. В этом случае полная ширина функции разрешения будет в Ö2 раз больше отдельных вкладов и для приведенного выше примера составит 0.0005.

Поскольку эффективная ширина импульса на фурье-дифрактометре не зависит от длины волны, то также как на импульсных источниках с длинным импульсом R_t ~ 1/d. После учета геометрического вклада, для ширины функции разрешения получается зависимость, показанная на рис. 5-12.