Дифракция нейтронов на поликристаллах

7.1. Особенности нейтронных экспериментов с поликристаллами.

В случае дифракции на поликристалле для получения связи структурных факторов с измеряемой интенсивностью, сечение когерентного рассеяния (3.9) необходимо усреднить по ориентациям вектора H, что приводит к следующему выражению:

s(H) = (2p)²/(V_ckH) 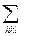j_hkl·|F_hkl|² δ(ksinθ - πH), (7.1)

где s(H) – дифференциальное сечение одной элементарной ячейки в единичный интервал волновых векторов k, j_hkl – фактор повторяемости кристаллографической плоскости (hkl). Аргумент δ-функции вместо векторного в (3.9) стал скалярным и приравнивая его нулю можно сразу получить уравнение Вульфа-Брэгга. Переходя к интенсивностям дифракционных пиков, т.е. интегрируя δ-функцию в (7.1) по k и вводя функцию j, описывающую форму дифракционного пика, можно получить следующее общее выражение:

I(d) ~ F(d) 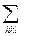j_hkl·Q_L·|F(H_hkl)|²j(d_hkl-d), (7.2)

где d – межплоскостное расстояние (d=1/H), F – поток нейтронов на образце, Q_L – фактор Лоренца. Здесь интенсивность спектра записана как функция межплоскостного расстояния, хотя в качестве переменной можно использовать угол рассеяния или время пролета. Выражения для факторов Лоренца различаются для l₀- и TOF-дифрактометров и зависят от геометрической формы образца. Например, для цилиндрического образца, диаметр которого меньше ширины первичного пучка:

Q_L(θ) = λ³/(V_c²·sinθ·cos2θ), (7.3)

Q_L(λ) = λ⁴/(V_c²·sin³θ), (7.4)

для l₀- и TOF-дифрактометров, соответственно.

Сложность решаемых на дифрактометре для поликристаллов структурных задач и прецизионность получаемых результатов определяется, прежде всего, достигнутым уровнем разрешения по межплоскостному расстоянию. Практика нейтронных структурных экспериментов показала, что при R(d) ≈ 0.01 (низкое разрешение) речь может идти только об уточнении координат атомов не очень сложных структур с объемом элементарной ячейки до ~200 ų. Иногда удается уточнить факторы заселенности и изотропные тепловые параметры отдельных атомов. Уровень R(d) ≈ 0.003 (среднее разрешение) позволяет провести независимое уточнение координат, факторов заселенности и изотропных тепловых параметров атомов. Наконец, если R(d) ≈ 0.001 (высокое разрешение), то как сложность структуры, так и точность результата становятся сравнимыми с имеющимися в случае эксперимента с монокристаллом.

7.2. Метод Ритвельда в структурной нейтронографии.

При уточнении структуры общепринятым методом для обработки измеренного дифракционного спектра от поликристалла в настоящее время является метод Ритвельда (Rietveld), сформулированный впервые в конце 60-х годов именно для анализа нейтронных данных [18]. Подробное описание этого метода, включающее особенности уточнения нейтронных данных, содержится в книге [19]. Напомним коротко его основные особенности.

Основной идеей метода является введение параметрического описания интенсивности измеренного дифракционного спектра, с последующим использованием метода наименьших квадратов (или каких либо других методов минимизации функционалов) для уточнения величин параметров. Функционал от параметров обычно записывается в виде:

c² = 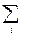w_i (I_{exp, i} - I_{cal, i})², (7.5)

где w_i - вес i-й точки, I_exp и I_cal – экспериментальное и рассчитанное значения интенсивности, сумма берется по точкам измеренного спектра в каком-то интервале межплоскостных расстояний d_i. Расчет I_cal ведется по формуле, следующей из (7.2):

I_cal(d_i) = C 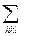j_hkl|F_hkl|²Q_L·j(d_hkl-d_i) + I_b(d_i), (7.6)

где C – нормирующая постоянная, I_b – интенсивность некогерентного фона. Все характеристики атомов кристалла входят в структурные факторы F_hkl, которые в изотропном по тепловым колебаниям приближении рассчитываются в соответствии с (3.11):

F_hkl = b_jr_jexp(2pi(hx_j+ky_j+lz_j))exp(-B_j/8d_hkl²), (7.7)

где b_j - когерентные длины рассеяния, r_j - фактор, определяющий количество атомов сорта j в ячейке (он же при необходимости является параметром, учитывающим заполнение позиции), (x,y,z,B)_j - относительные координаты и тепловой параметр j-го атома. Параметрами, уточняемыми при минимизации функционала (7.5), являются наборы (r_j,x_j,y_j,z_j,B_j) атомов, фоновая интенсивность (зачастую ее можно описать многочленом степени не выше четвертой) и параметры элементарной ячейки кристалла, которые входят в выражение для d_hkl = 1/H_hkl.

Практика структурного анализа дифракционных данных от поликристаллов с применением метода Ритвельда показывает, что если R слабо зависит от d_hkl, то число пиков, которые имеет смысл включать в рассмотрение составляет приблизительно (3R)^-1 для структур со средним уровнем симметрии. Предполагая необходимым пятикратное превышение числа пиков над числом уточняемых параметров, получим, что при R = 0.001 одновременно можно уточнять до 70 структурных параметров, т.е. координат, факторов заселенности и тепловых параметров атомов.

Существуют несколько пакетов программ, в которых метод Ритвельда реализован для обработки нейтронных дифракционных спектров. Наиболее популярными являются пакеты FullProf (J. Rodriguez-Carvajal, [20]) и GSAS (R.B. Von Dreele, [21]), в которых реализованы возможности обработки спектров, измеренных на l₀- и TOF-дифрактометрах, а также учет как ядерного, так и магнитного рассеяния. На рис. 7-1показан результат обработки по методу Ритвельда с использованием программы FullProf спектра, измеренного на дифрактометре HRPT (SINQ). Разностная функция (I_{exp, i} - I_{cal, i}), показанная в нижней части рисунка, флуктуирует около нуля, что говорит о хорошем соответствии между моделью и реальной структурой этого кристалла.

Достигаемая с помощью метода Ритвельда точность определения структурных параметров может быть очень высокой. На рис. 7-2показаны зависимости от температуры межатомных расстояний Mn-O (слева) и валентных углов Mn-O-Mn (справа) в соединении (La_0.25Pr_0.75)_0.7Ca_0.3MnO₃ (LPCM-75), обогащенном изотопами кислорода ¹⁶О (синие значки) и ¹⁸О (красные значки), полученные по результатам эксперимента на HRFD (ИБР-2). В этих составах в зависимости от содержания изотопов кислорода реализуются разные низкотемпературные состояния: состав с ¹⁸О становится антиферромагнитным, в составе с ¹⁶О возникает смешанное AFM + FM состояние, с преобладанием ферромагнитной фазы. Видно, что в составе с ¹⁶О расстояние Mn-O1 меньше, а валентный угол Mn-O1-Mn больше, чем в составе с ¹⁸О. Несмотря на то, что абсолютные отличия очень малы (0.006 Å и 0.8°), они уверенно фиксируются благодаря достигнутой точности определения параметров.

7.2.1. Форма пика. Одним из факторов, определяющих успех анализа структуры по методу Ритвельда, является корректное задание формы дифракционного пика, т.е. функции j(d_hkl-d) во всей области изменения d_hkl. Успех этого метода на ранних стадиях его использования для обработки нейтронных дифракционных спектров от поликристаллов был во многом связан с более простой формой именно нейтронных пиков, по сравнению с пиками, измеряемыми на рентгеновских дифрактометрах. Однако ситуация значительно усложнилась с появлением больших ПЧД и улучшением разрешающей способности нейтронных дифрактометров. Т.к. форма пика и ее функциональная зависимость от d_hkl заметно различается для разных типов нейтронных дифрактометров, то ее следует рассмотреть раздельно.

l₀-дифрактометр. В качестве начального приближения для формы пика на l₀-дифрактометре выбирается гауссова функция, зависимость ширины которой от угла рассеяния определяется формулами (5.16) - (5.19). Этого приближения, как правило, достаточно, если дифрактометр обладает средним разрешением и если углы рассеяния не малы. Отклонения от симметричной гауссовой формы обычно связаны с особенностями отражения от монохроматора, приводящим к появлению некоторой асимметрии при малых (<20°) углах рассеяния. Ее учет проводится введением эмпирической поправки, включенной в стандартные программные пакеты (см., например, [20]). Еще одним усложняющим обстоятельством является присутствие лоренцевского вклада, который учитывается либо вычислением свертки гауссиана и лоренциана (функция Войта), либо сложением этих двух функций с некоторым весом (псевдо-функция Войта). При обработке спектра, показанного на рис. 7-1, форма пика задавалась с помощью последнего варианта.

TOF-дифрактометр. Дифракционные пики, измеряемые на TOF-дифрактометре, расположенном на SNS-источнике с коротким импульсом, как правило, имеют сильно асимметричную форму. Это связано с тем, что форма импульса тепловых нейтронов определяется сверткой импульса быстрых нейтронов от источника, G₁(t), и функции, описывающей процесс замедления, G₂(t). Обычно вклад источника можно с хорошей точностью представить как гауссову функцию, т.е. G₁(t) ~ exp(-t²/2s₁²). Отклик замедлителя можно представить в виде двух экспонент: G₂(t) ~ exp(-t/a₁) при t < 0 и G₂(t) ~ exp(-t/a₂) при t > 0. Вследствие того, что a₁ << a₂, левое и правое крылья этой функции сильно различаются. Результирующее распределение, являющееся сверткой G₁(t) и G₂(t), представляется довольно сложной параметрической функцией, описание которой приведено в [19]. Угловой вклад в результирующую функцию хорошо аппроксимируется гауссианом и его учет не изменяет формы пика, лишь несколько увеличивая ширину.

Основной проблемой задания формы пика в случае TOF-дифрактометра на источнике типа SPS является введение правильной функциональной зависимости от d параметров в R(t). В первом приближении от d зависит только параметр a₂ в G₂(t), причем a₂ ~ d. Более тщательные исследования показали, что в широком интервале d зависимость a₂(d) не удается описать аналитически и ее приходится задавать численно для конкретного типа замедлителя. Для LPS-источника с шириной исходного импульса более 300 мкс вклад замедлителя почти не заметен, вследствие чего и ширина, и форма импульса слабо изменяются в широком интервале межплоскостных расстояний.

Фурье-дифрактометр. В этом случае временная часть функции разрешения описывается формулой (5.27) и, соответственно, зависит от частотного распределения g(n). Наименьшей ширина функции R(t) получается, если g(n) = const, при n ≤ n_max, но при этом R(x) ~ sin x/x и имеет несколько отрицательных минимумов (кривая 1 нарис. 7-3). Для устранения этого эффекта в частотное распределение вводятся корректирующие слагаемые, в частности используется распределение Блэкмана

g(u) = 1 + pcospu +qcos2pu, (7.8)

где u = n/n_max, p = 1.03 и q = 0.08. В этом случае функция разрешения несколько расширяется, но отрицательные минимумы практически полностью исчезают (кривая 2 нарис. 7-3). Реально измеряемая на фурье-дифрактометре форма пика зависит от настройки фазы электронного сигнала от фурье-прерывателя и, как правило, демонстрирует небольшую асимметрию, которую трудно учесть аналитически.

Облегчающим обстоятельством является то, что результирующая функция разрешения практически не зависит от d. Соответственно ее можно задать численно, предварительно измерив с хорошей статистикой с помощью модельного образца. В программном пакете MRIA [22], основной задачей которого является обработка спектров, измеренных на фурье-дифрактометре, используется именно такая опция.

На рис. 7-4 показан дифракционный спектр того же образца, что и приведенный на рис. 7-1, измеренный на фурье-дифрактометре HRFD.

Вклад образца. Форма измеряемых дифракционных пиков является сверткой функции разрешения и сечения рассеяния кристалла (формула (5.3)). Если кристалл имеет бесконечную длину когерентности и отсутствует дисперсия параметров его элементарной ячейки, то сечение когерентного рассеяния пропорционально δ-функции (формула (3.8)), и из (5.3) следует, что I(k) ~ R(k). Т.е. измеряя форму пиков от такого кристалла можно определить функцию разрешения дифрактометра в зависимости от вектора kдля монокристалла и от модуля k для поликристалла.

В реальном кристалле одно из этих условий или оба вместе нарушаются, и дифракционные пики уширяются, как говорят, за счет вклада образца. Еще одной причиной уширения могут быть большие геометрические размеры образца. Как эти факторы сказываются на дифракционных пиках, измеряемых на l₀-дифрактометре, подробно описано в литературе, см., например, [16]. Поэтому рассмотрим подробнее только ситуацию с шириной дифракционных пиков, измеряемых на TOF-дифрактометре.

Пренебрегая в формуле (5.23) членом (который обычно мал), учитывающим неопределенность в пролетном расстоянии получаем для ширины пика, определяемой только функцией разрешения дифрактометра:

Dd² = [(Dt₀/t)² + (Dq/tgq)²]·d², (7.9)

где Dt₀ – ширина импульса источника, которая может зависеть от d, t – полное время пролета от источника до детектора, Dq включает все геометрические неопределенности. Вклад в ширину, связанный с неопределенностью в параметрах элементарной ячейки, есть (Dd)_с = (Da/a)·d, где под Da/a понимается среднее относительное изменение параметра. В случае анизотропного уширения или сжатия необходимо учесть зависимость (Dd)_с от направления в решетке, т.е. от индексов Миллера. Вклад в ширину дифракционного пика из-за конечного размера когерентных блоков есть: (Dd)_s = (DH/H)·d, где DH = const = 0.62/L, L – характерный размер блока. Т.к. H = 1/d, то (Dd)_s = (0.62/L)·d². В предположении, что различные вклады в ширину пика складываются квадратично (что не всегда верно), функциональная зависимость ширины пиков от межплоскостного расстояния при измерении дифракционного спектра на TOF-дифрактометре можно записать как:

Dd ² = C₁ d ² + C₂ d ² + C₃ d ⁴, (7.10)

где C₁ – величина в квадратных скобках в (7.9) (в случае источника типа SPS она в первом приближении не зависит от d), C₂ = (Da/a)², C₃ = (0.62/L)².

Вычитая из Dd² вклад функции разрешения, т.е. слагаемое C₁d², получаем для квадрата относительной ширины:

(Dd/d)² = C₂ + C₃ d ² = (Da/a)² + (0.62/L)² d ² , (7.11)

т.е. линейную функцию d, параметры которой позволяют определить среднюю дисперсию параметров ячейки и характерный размер когерентных блоков.

Анализ спектров, измеренных на нейтронных дифрактометрах высокого разрешения, как правило, позволяет легко определять вклад образца в полную ширину пиков. В том числе, возможен анализ эффектов анизотропного уширения. В качестве примера на рис. 7-5 показаны зависимости величины Dd² от d² для разных индексов l. В соответствии с формулой (7.10) наблюдаются квадратичные зависимости, определение параметров которых позволяет получить оценку размеров когерентных областей по разным направлениям: в плоскости (ab) – L_ab = (350 – 400) Å, в перпендикулярном направлении – L_c = (120 – 150) Å. Такая дискообразная форма кристаллитов естественна для слоистой атомной структуры b-Ni(OH)₂ и наблюдалась с помощью электронной микроскопии.

7.3. Эксперименты в реальном времени.

Специфические особенности нейтронографии делают ее исключительно мощным методом изучения необратимых переходных процессов в конденсированных средах. Целенаправленные, систематические эксперименты такого типа (в литературе они получили название RT (Real Time - эксперименты) начались сравнительно недавно, но уже можно сказать, что сформировалась новая ветвь нейтронографии - дифрактометрия в реальном времени, под которой понимается наблюдение с помощью рассеяния нейтронов перестройки структуры на атомном уровне непосредственно в ходе переходного процесса. В общем случае в большинстве экспериментов регистрируются только дифракционные спектры, являющиеся наиболее интенсивной компонентой процесса рассеяния, хотя все шире используется совместный анализ дифракции, малоуглового и диффузного рассеяния. По сравнению с дифракцией рентгеновского или синхротронного излучений, также широко применяемых для наблюдения переходных процессов, нейтронография в реальном времени сохраняет все достоинства, присущие нейтронам. Часто при постановке экспериментов в реальном времени немаловажным фактором является высокая проникающая способность нейтронов.

Масштаб времен, доступных для изучения, характеризуется временем (t_s) измерения одного спектра с достаточным для целей эксперимента уровнем статистики. Величина t_s зависит от потока нейтронов в первичном пучке, рассеивающей способности образца и телесного угла детектора. Естественно, что дифрактометрия в реальном времени может рассматриваться как отдельный метод, если t_s не слишком велико. Для его уменьшения требуется оптимизация дифрактометра по светосиле и, соответственно, компромисс с разрешающей способностью, который достигается тем, что она выбирается низкой или средней. При этом, акцент в измерении дифракционного спектра смещается в область средних и больших d_hkl, где это разрешение оказывается достаточным.

Примером современной установки для проведения RT-экспериментов является дифрактометр D20 на реакторе в ILL [23]. При сравнительно хорошем разрешении на D20 можно набрать необходимую статистику в течение нескольких минут, а иногда и нескольких секунд (рис. 7-6). Его высокая светосила обусловлена рекордным потоком нейтронов от реактора (Φ₀ = 1.5∙10¹⁵ н/см²/с), монохроматором с вертикальной фокусировкой (поток монохроматических нейтронов до ~10⁸ н/см²/с), оптимальным выбором коллимации первичного пучка нейтронов и большим телесным углом детектора (детектор охватывает 154° по 2θ и высоту входного окна 150 мм). Существуют проекты увеличения телесного угла детекторов такого типа за счет расширения высоты входного окна детектора [24]. Сохранение приемлемого уровня разрешения обеспечивается позиционной чувствительностью вертикальных нитей, т.е. детектор фактически является двухкоординатным.

На реакторе ИБР-2, обладающим рекордным потоком среди импульсных источников, имеются возможности для анализа необратимых процессов в кристаллах с временным разрешением на уровне нескольких минут, а в благоприятных случаях вплоть до нескольких секунд. Рассмотрим, какая информация была получена при изучении фазового перехода в шпинельной структуре CuFe₂O₄, легированной Li и V. При высокой температуре (Т_с ≈ 750 К) в этом составе происходит структурный переход из высокотемпературной симметричной кубической (пр. гр. Fd3m) фазы в тетрагональную (пр. гр. I4₁/adm), связанный с кооперативным эффектом Яна-Теллера. Эксперимент был проведен на TOF-дифрактометре ДН-2, в режиме непрерывного изменения температуры с регистрацией спектров каждые 80 с. Изменение температуры во времени и характерные дифракционные спектры показаны на рис. 7-7. При нагревании происходил переход из кубической фазы в тетрагональную, при охлаждении – обратный переход, что хорошо видно по форме отдельных пиков. Анализ измеренных спектров по методу Ритвельда позволил получить полную картину перехода (рис. 7-8): изменения параметров элементарной ячейки, координат атомов, факторов заселенности позиций. Неожиданным эффектом было наблюдение резкого и обратимого изменения ширины дифракционных пиков при переходе. Зависимость этого эффекта от d_hkl указывает на то, что его причиной являются внутренние напряжения, возникающие при образовании двойниковой структуры при переходе в низкосимметричную фазу.

Одной из уникальных особенностей TOF-дифрактометра, особенно важной для RT-экспериментов, является сравнительно простая возможность одновременного измерения спектров дифракции и малоуглового рассеяния нейтронов (МУРН). Хорошая коллимация первичного пучка позволяет использовать детекторы, установленные на малых углах рассеяния на небольшом расстоянии от образца. Благодаря широкому спектру первичного пучка диапазон переданных импульсов получается достаточно большим.

В качестве примера, на рис. 7-9 показаны спектры дифракции и МУРН, измеренные в ходе фазовых превращений в BiSrCaCu₂O_x, вызванных изменением температуры. Для дифракционных спектров показан интервал больших межплоскостных расстояний, при которых регистрируются пики (002) от фаз Bi-2201 (при d ≈ 12 Å) и Bi-2212 (при d ≈ 15 Å). Спектры МУРН регистрировались в диапазоне переданных импульсов Q ≈ 0.02 – 0.06 Å^-1, что соответствует характерным расстояниям ~200 – 600 Å. В исходном состоянии образец находился в аморфной фазе, полученной быстрой закалкой после плавления. При нагревании произошла кристаллизация, причем сначала появилась фаза Bi-2201, которая затем переходила в фазу Bi-2212. После плавления и медленного охлаждения обе фазы появлялись почти одновременно. Хорошо видна четкая корреляция изменений, происходящих в дифракционных и малоугловых спектрах. Очень интенсивное малоугловое рассеяния, возникающее непосредственно перед кристаллизацией фазы Bi-2201, свидетельствует о нуклеационном механизме ее образования.

7.3.1. Предельные возможности для RT-экспериментов на импульсном источнике нейтронов.В рассмотренных примерах RT-экспериментов время измерения одной нейтронограммы составляло от нескольких секунд до минут, т.е. информация набиралась за 10 и больше импульсов реактора ИБР-2 (его период повторения 0.2 с). Расчеты показывают, что, в принципе, на ИБР-2 в некоторых случаях необходимую статистику можно набрать от одного импульса мощности, и это подтверждает результат модельного эксперимента, показанный на рис. 7-10 (Г.М.Миронова, 1988). Из сравнения нейтронограмм, представленных на рис. 7-10, видно, что хотя статистическая точность в спектре, измеренном от одного импульса мощности реактора, невелика, все характерные особенности дифракционной картины фиксируются достаточно надежно.

Этот результат говорит о том, что при изучении необратимых процессов временное разрешение 20 - 200 мс (периоды повторения источников) может быть достижимо, что еще недавно казалось совершенно нереальным для нейтронографии. Однако ситуация, когда одной вспышки оказывается достаточно для набора статистики, в принципе, позволяет продвинуться еще дальше по уменьшению t_s. Действительно, если дифракционные спектры регистрируются многодетекторной системой с интервалом по углу рассеяния Dq (рис. 7-10), то в соответствии с уравнением Вульфа-Брэгга в соседних детекторах дифракционный пик смещается по длине волны на Dl = 2dcosqDq. При пролетном расстоянии 25 м, это эквивалентно сдвигу по времени на Dt ≈ 18Dq мс при d=2 Å и 2q=90°. T.e. несколько детекторов, поставленных в области углов рассеяния 90° со сдвигом ~3° будут регистрировать один и тот же дифракционный пик со сдвигом по времени в ~1 мс.

Эта величина, по-видимому, близка к предельному временному разрешению в нейтронографии необратимых процессов на импульсных источниках нейтронов. Она сравнима с величинами, достигнутыми на источниках синхротронного излучения и существенно меньше, чем пределы, достижимые на стационарных реакторах.

7.4. Эксперименты с высоким внешним давлением.

До конца 1980-х годов область применения нейтронных методов при исследовании поведения вещества при высоких давлениях, как правило, ограничивалась диапазоном до 2 ГПа, что связано с использованием относительно больших объемов образца (~1 см³) в камерах давления типа поршень-цилиндр. Применение для достижения больших давлений алмазных или сапфировых наковален, что обычно для источников рентгеновского или синхротронного излучения, казалось совершенно невозможным из-за малого (~1 мм³) объема образца и относительной слабости потоков от нейтронных источников. Однако развитие методов фокусировки нейтронных пучков и создание детекторов с большим телесным углом позволили расширить диапазон давлений в этих экспериментах до нескольких десятков ГПа. Первые эксперименты с образцами в камерах с наковальнями были проведены в РНЦ КИ при давлениях до 10 ГПа с использованием монокристаллов сапфира и выше 30 ГПа в камерах с алмазными наковальнями (рис. 7-11). Сапфировые и алмазные наковальни оптически прозрачны, поэтому давление в камере можно определять по сдвигу линии флюоресценции рубина. Впоследствии опыт этих экспериментов был перенесен на ИБР-2 и на реактор в LLB (Сакле), где были получены рекордные результаты по минимальному объему образца и уровню достигнутых давлений.

На рис. 7-12 показана конструкция дифрактометра ДН-12 на реакторе ИБР-2. Его главной особенностью является кольцевая многодетекторная система, обладающая большим телесным углов и позволяющая регистрировать дифракционные спектры в широком диапазоне d_hkl. На ДН-12 выполнены эксперименты с образцами объемом около 1 мм³ при давлениях до 7 ГПа, в частности, с галогенидами аммония ND₄X и NH₄X (X = F, Cl, Br, I), интерметаллидами марганца Mn₂Sb и MnAs, сложными оксидами марганца R_1-xA_xMnO₃ (R = La, Pr; A = Ca, Sr, Na) и др.

Другой подход, в котором для задания давления применяется малогабаритный 250-тонный пресс с тороидальной ячейкой из карбида вольфрама, был реализован в работах франко-английской группы на импульсных источниках ISIS и LANSCE. Этой группе удалось достичь давлений до 12 ГПа при объеме образца ~100 мм³ и даже 26 ГПа, если объем образца уменьшался до ~35 мм³ и использовалась ячейка из спеченного алмаза.

7.5. Анализ локальной структуры.

Появление SNS источников с коротким импульсом (SPS типа) позволило существенно продвинуться в дифракционных исследованиях эффектов локального беспорядка в структуре кристаллов. Идея метода, который получил название PDF (Pair Distribution Function technique), состоит в анализе полной функции рассеянияизлучения на кристалле, которое включает помимо когерентных брэгговских пиков еще и диффузную компоненту. Как следует из рассмотрения, проведенного в разделе 3.4, информация об идеально упорядоченной структуре содержится в интенсивностях брэгговских пиков. Если же дальний порядок нарушается, то дополнительно возникает диффузное рассеяние в виде более-менее гладкого распределения интенсивности. Оказывается, что совместный анализ когерентного и диффузного рассеяния позволяет получить информацию о распределении межатомных расстояний непосредственно в реальном пространстве. Далее проводится сравнение экспериментального и вычисленного на основе моделей распределений, что и дает сведения о возможном локальном нарушении структуры кристалла. Подробное изложение этого метода приведено в сборнике статей [25] и в обзоре [26].

Математически метод основан на фурье-преобразовании полной интенсивности упруго рассеянных нейтронов S(Q), Q = 4π∙sinθ/λ = 2π/d – переданный импульс, что приводит к парной корреляционной функции:

G(r) = 2/π·∫Q[S(Q) – 1]sin(Qr)dQ, (7.12)

где S(Q) предполагается исправленной на фон и другие методические факторы и отнормированной на поток нейтронов и на количество атомов в образце. Предполагается также, что поликристаллический образец рассеивает нейтроны изотропно, что позволяет свести трехмерное преобразование Фурье S(Q) в G(r) к одномерному интегралу по модулю Q. В идеальном варианте интеграл в 7.12должен вычисляться от 0 до бесконечности, но реально есть экспериментальное ограничение как по минимальному, так и по максимальному наблюдаемым переданным импульсам. Эти ограничения (“ошибка обрыва интеграла”) приводят к эффектам аналогичным уширению дифракционных пиков из-за конечного размера когерентных блоков кристалла, а именно, пикообразные распределения межатомных расстояний уширяются и их детали могут оказаться утерянными.

Из формулы для Q следует, что для его увеличения необходимо проводить измерение спектра на угле рассеяния близком к 180º и использовать нейтроны с малой длиной волны. Практика применения метода PDF показала, что в кристаллах интересные с точки зрения локальных нарушений дальнего порядка эффекты наблюдаются, если Q_max ≈ 25 Å^-1 и больше. Это означает, что дифракционный спектр должен быть измерен до d ≈ 0.2 Å. Столь малые межплоскостные расстояния с приемлемой статистикой и разрешением могут быть измерены только на нейтронных источниках SPS типа.

Функцию F(Q) = Q[S(Q) – 1] принято называть приведенным структурным фактором. Ее вид для простого случая порошка Ni показан на рис. 7-13. Видно, что в этом случае эксперимент был проведен до Q_max ≈ 30 Å^-1 и даже при максимальных Q наблюдаются структурные эффекты. Полученная с помощью преобразования Фурье 7.12функция G(r) по существу является альтернативным представлением дифракционных данных, переведенных из обратного пространства в кристаллическое. Преимуществом этого представления является удобство сравнения G(r) с модельными расчетами, включающими локальный беспорядок в структуре кристалла. Это сравнение может быть оформлено как процедура минимизации функционала по параметрам, полностью аналогичная методу Ритвельда (рис. 7-13). Процедура оформлена в виде программы PDFgetX2, доступной по ссылке [27].

Помимо выполнения условия регистрации спектра до больших переданных импульсов (иногда необходимо измерять спектр до Q_max ≈ 75 Å^-1), успешное применение метода PDF требует тщательной организации эксперимента. Прежде всего, это относится к измерению или учету эффектов, могущих имитировать диффузное рассеяние, таких как некогерентный фон, многократное рассеяние в образце, самоэкранировка из-за поглощения и некоторых других.

Появление необходимой экспериментальной техники на нейтронных и синхротронных источниках и развитие вычислительных методов уже позволили использовать PDF анализ для решения большого числа интересных проблем, связанных с наличием локального беспорядка структуры. В частности, было выполнено множество исследований высокотемпературных сверхпроводников и манганитов с эффектом CMR, в которых локальные нарушения структуры зачастую играют важную роль в формировании их физических свойств. На рис. 7-14показан небольшой участок функции G(r) для сложного оксида марганца La_0.75Ca_0.25MnO₃. Этот состав при низкой температуре находится в ферромагнитной (FM) фазе, которая характеризуется регулярной формой октаэдров MnO₆. Применение метода PDF позволило выяснить, что выше температуры перехода в FM фазу образец находится в смешанном состоянии, включающем регулярные и искаженные октаэдры. При низкой температуре доминирует регулярная фаза, но остается некоторая доля искаженной фазы.