Рассеяние плоской волны на периодической структуре.

Прежде чем изложить квантовомеханический подход к проблеме дифракции нейтронов на кристалле, рассмотрим схему, лежащую в основе решения задачи о дифракции излучения на кристалле. В своих основных моментах она одинакова для любого типа излучения, хотя некоторые эффекты зависят от конкретных особенностей излучения и его взаимодействия с кристаллом.

Пусть име­ет­ся объ­ект, к ко­то­ро­му при­вя­за­на си­с­те­ма ко­ор­ди­нат {x,y,z} и на ко­то­ром рассе­и­ва­ет­ся пло­ская во­л­на exp(ik₁r), где k₁ – ее волновой вектор. В уда­лен­ной точке R рас­се­ян­ная на центре, находящемся в начале ко­ор­ди­нат, во­л­на f бу­дет ~exp(ik₂R), k₂ – волновой вектор рассеянной волны. Рассеяние предполагается упругим, т.е. |k₁|=‌‌|k₂|= 2π/λ. При рас­се­я­нии на центре, находящемся в точке r,возникает дополнительная разность фаз (рис. 3-2), т.е. f ~ exp(ik₂R)×exp[i(k₂-k₁)r]. В предположении, что объект состоит из N рассеивающих центров, и все рассеянные волны складываются, полная амплитуда рассеянной волны получится суммированием:

f ~ exp(ik₂R) f(r_j)exp(ikr_j), (3.1)

где f(r_j) - амплитуда рассеяния центром, находящемся в точке r_j, k= k₂ - k₁ – вектор рассеяния, сумма берется по всем рассеивающим центрам.

Пусть теперь вместо одного объекта имеет место некоторая сумма из N объектов, положения которых в общей системе координат фиксируются векторами R_m (рис. 3-3), тогда вместо (3.1) имеем соотношение

f ~ exp(ik₂R) exp(ikR_m) 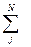f(r_j)exp(ikr_j), (3.2)

где суммирование по j проводится внутри m-го объекта, состоящего из N центров, а затем выполняется суммирование по всем M объектам. Общий фазовый множитель exp(ik₂R) можно опустить и тогда:

f ~ F(R_m)exp(ikR_m), (3.3)

где F(R_m) = 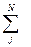f(r_j)exp(ikr_j) – описывает рассеяние на m-м объекте.

Если рассеяние идет на кристалле, то m-м объектом является элементарная ячейка кристалла, a вектора R_m проведены в какую-то фиксированную точку элементарной ячейки. В силу периодичности структуры кристалла все ячейки одинаковы, т.е. F(R_m) = const и не зависит от номера объекта (ячейки). Формулу (3.3) можно в этом случае переписать так:

f ~ F∙ exp(ikR_m), где F = 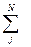f_jexp(ikr_j), (3.4)

где r_j – координаты, a f_j - амплитуда рассеяния j-го атома в элементарной ячейке сумма берется по всем атомам ячейки. Величина F называется структурным фактором (иногда – структурной амплитудой) элементарной ячейки.

Можно показать, что для кристалла, состоящего из большого числа ячеек, т.е. при M → ∞, с хорошим приближением

exp(ikR_m) = d(k- 2pH), (3.5)

где d есть дельта-функция Дирака, H= H_hkl = ha*+kb*+lc* -вектор, проведенный в узел обратной решетки кристалла (h, k, l - индексы Миллера), т.е.

f ~ F×d(k- 2pH) (3.6)

и, следовательно, интенсивность рассеяния будет отлична от нуля только, если k= 2pH. Соответствие суммы по m и дельта-функции можно понять, если учесть, что вектора R_m являются векторами трансляций в прямой решетке и следовательноH_hkl×R_m = n, где n - целое число. Подставляя в показатель экспоненты 2pH вместо k и вспоминая, что сумма экспонент с показателями вида 2pni, при n ® ¥ дает d-функцию, приходим к (3.6).

Итак, амплитуда рассеянной на кристалле волны f ~ F_H×d(k- 2pH), где
F_H = 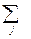f_jexp(2piHr_j) – структурный фактор, и эта формула в принципе определяет большинство основных моментов, связанных с дифракцией на кристалле любого типа излучения. При проведении структурного анализа специфика типа излучения проявляется почти исключительно в природе величин f_j в формуле для структурного фактора.

3.3. Квантовомеханическое рассмотрение дифракции нейтронов.

Квантовомеханическое рассмотрение задачи рассеяния предполагает решение уравнения Шредингера с заданным потенциалом взаимодействия нейтрона с атомами. В курсах нейтронной физики (см., например, [1]) показывается, что эта задача может быть решена в рамках первого борновского приближения, если используется специальный вид потенциала взаимодействия с ядром атома, так называемый псевдопотенциал Ферми:

V(r) = -2πħ²·(f_j/M_j)·d(r- r_j), (3.7)

где f_j – амплитуда рассеяния на j-м атоме с массой M_j, находящегося в точке r_j. Условием применимости псевдопотенциала Ферми и первого борновского приближения является малость амплитуды рассеяния по сравнению с длиной волны нейтрона: |f| << λ. Поскольку |f| ~ 10^{-12 см, а λ ~ 10-8 см, то указанное приближение заведомо справедливо.}

Борновское приближение дает возможность получить выражение для дважды дифференциального сечения рассеяния d²σ/dΩdε, т.е. вероятность того, что нейтрон будет рассеян в элемент телесного угла dΩ при определенном изменении энергетического состояния кристалла и волнового вектора нейтрона. При упругом рассеянии энергия нейтрона сохраняется, т.е. можно совершить переход d²σ/dΩdε → dσ/dΩ. Прямой расчет с потенциалом (3.7) приводит к следующему выражению для упругого сечения рассеяния на кристалле с жестко закрепленными ядрами, т.е. без учета теплового движения [1]:

dσ/dΩ = {1/N 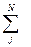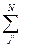b_jb_j'·exp[ik(r_j -r_j')]}·{1/M 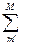exp[ik(R_m -R_m')]}, (3.8)

где суммирование по j и j′ проводится внутри элементарной ячейки, включающей N атомов, суммирование по m и m′ проводится по всем M элементарным ячейкам. Можно показать, что при M → ∞, второй сомножитель в (3.8) превращается в (8π³/V_c)·d(k- 2pH), где V_c – объем элементарной ячейки. Следовательно, можно написать, что

dσ/dΩ = (8π³/V)·|F_H|²·d(k- 2pH), (3.9)

где F_H = 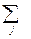b_jexp(ikr_j) – структурный фактор. Таким образом, квантомеханический расчет привел к выражению аналогичному (3.6), но с более ясным физическим смыслом и с точным числовым коэффициентом. Наличие функции d(k- 2pH) в (3.9), полученной в предположении бесконечных размеров кристалла по всем направлениям, означает, что сечение когерентного рассеяния отлично от нуля только при строгом выполнении условия k= 2pH. В случае конечных размеров кристалла, d-функцию следует заменить на результат вычислений второго сомножителя в (3.8). Отвлекаясь пока от деталей вычислений можно переписать (3.9) в более общем виде:

dσ/dΩ = (8π³/V)·|F_H|²·j(k- 2pH), (3.10)

где j(k- 2pH) – некоторая функция, вид которой в обратном пространстве зависит от размеров кристалла (точнее от длины когерентности) в том или ином направлении, дисперсии параметров элементарной ячейки, мозаичности кристалла. Сечение рассеяния при этом будет отлично от нуля в некоторой окрестности узлов обратной решетки, что формально можно рассматривать как проявление конечных размеров узлов. Следует еще отметить, что формулы (3.6), (3.9) и (3.10) получены в так называемом кинематическом приближении, т.е. с пренебрежением вклада от процессов многократного рассеяния. Строгое рассмотрение этих процессов (динамическая дифракция) приводит к существенной модификации вида сечения когерентного рассеяния. Например, даже в случае очень больших размеров кристалла, ширина дифракционного пика остается конечной (так называемый “столик Дарвина”).

Рассмотрение рассеяния нейтронов на кристалле с учетом теплового движения атомов требует решения нестационарного уравнения Шредингера. Оказывается, что выражение (3.9) для сечения рассеяния остается без изменений, но в формуле для структурного фактора появляется дополнительный множитель, называемый тепловым фактором или фактором Дебая-Валлера, а именно:

F_H= 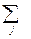b_jexp(2piHr_j)∙exp(-W_j), (3.11)

где вектор рассеяния kзаменен на 2pH в соответствии с тем, что сечение когерентного рассеяния не равно нулю только, если k= 2pH, exp(-W_j) – фактор Дебая-Валлера, в котором величины W_j относятся к конкретным атомам, зависят от H и от температуры кристалла.

При общем рассмотрении, помимо учета теплового движения, необходимо выполнить несколько типов усреднения сечения рассеяния: по исходным энергетическим состояниям рассеивателя, по спиновым состояниям ядра и нейтрона, по различным изотопам элементов и, если это требуется, по возможным ориентациям кристалла относительно нейтронного пучка. Эти действия рассматриваются в следующих параграфах.

3.4. Когерентное и некогерентное рассеяние нейтронов.

Идеальный дальний порядок в кристалле предполагает, что во всех элементарных ячейках, во всех эквивалентных кристаллографических позициях располагаются одинаковые атомы, т.е. атомы с одинаковой рассеивающей способностью. Только в этом случае обеспечивается постоянство фазовых соотношений между волнами, рассеянными атомами, расположенными в разных элементарных ячейках. Именно постоянство (отсутствие случайности) фаз рассеянных волн имеется в виду, когда говорят, что рассеяние когерентно. Когерентность процесса рассеяния дает возможность волнам конструктивно интерферировать и образовывать дифракционные максимумы при определенных соотношениях между переданным импульсом и вектором обратной решетки кристалла.

Однако при рассеянии нейтронов даже на идеальном с точки зрения кристаллографии кристалле полностью когерентное рассеяние оказывается почти для всех соединений принципиально недостижимым. Для этого есть две причины. Во-первых, в эквивалентных позициях могут находиться разные изотопы одного и того же элемента, во-вторых, ядро может иметь спин, ориентация которого случайна по отношению к спину налетающего нейтрона. Поскольку разные изотопы имеют, как правило, различающиеся длины рассеяния, которые к тому же зависят от взаимной ориентации спинов ядра и нейтрона, то в величине фаз рассеянных на эквивалентных атомах нейтронных волн появляется элемент случайности. Другими словами, рассеяние нейтронов будет полностью когерентно, только если в состав вещества кристалла входят изотопы только одного сорта со спином равным нулю.

В обычной ситуации, т.е. когда спины ядер и налетающих на них нейтронов направлены произвольно, а изотопы элемента распределены в кристалле случайным образом, необходимо провести усреднение сечений по направлениям спина и по содержанию изотопов. Оба эффекта – случайность в ориентации спина ядер и распределении изотопов – нарушают идеальный дальний порядок в кристаллах, вследствие чего помимо когерентного рассеяния, приводящего к образованию дифракционной картины, появляется некогерентный диффузный фон. Для описания этих эффектов вводятся когерентное и некогерентное сечения рассеяния, которые получаются при усреднении сечения рассеяния по изотопам и спиновым состояниям.

Для проведения усреднения будем исходить из следующего выражения для сечения рассеяния:

dσ/dΩ ~ 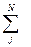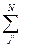<b_jb_j’>·exp[ik(r_j -r_j’), (3.12)

где суммирование предполагается по всем атомам рассеивателя, а усреднение (обозначенное скобками < >) затрагивает только длины рассеяния. Выражение (3.12) можно переписать в эквивалентном виде:

dσ/dΩ ~ 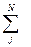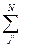<b_j><b_j’>·exp[ik(r_j -r_j’)] + 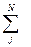<b_j²>, (3.13)

где из первой суммы исключены члены с j = j′ и записаны как второе слагаемое. В (3.13) добавим и вычтем 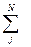<b_j>² и получим:

dσ/dΩ ~ 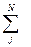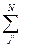<b_j><b_j’>·exp[ik(r_j -r_j’)] + 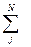[<b_j²> - <b_j>²], (3.14)

где теперь в первом слагаемом суммы включают все члены от 1 до N. Первое слагаемое содержит интерференционный множитель exp[ik(r - r¢)], оно пропорционально N², где N – число атомов в кристалле, и именно оно приводит к появлению узких дифракционных пиков. Интенсивность пиков определяется величинами b_coh = <b>, которые принято называть когерентными длинами рассеяния. Второе слагаемое не зависит от k, т.е. представляет собой гладкую функцию (фон), величина которого пропорциональна N и определяется флуктуациями амплитуд рассеяния. Величина b_inc = [<b²> - <b>²]^1/2 называется некогерентной длиной рассеяния.

Для усреднения по изотопному составу необходимо знать относительное содержание каждого изотопа. Например, в случае M изотопов, содержание которых составляет α_m, а соответствующие длины рассеяния есть b_m, получаем:

<b> = a_mb_m, <b²> = a_mb_m², (3.15)

причем a_m = 1.

Для усреднения по взаимным ориентациям спинов нейтрона и ядра, следует вспомнить, что проекция спина нейтрона (в единицах ħ) на выделенное направление s = 1/2 и, следовательно, возможны только две ориентации – спин нейтрона параллелен или антипараллелен спину ядра. Из законов квантовой механики следует, что веса этих двух состояний есть (S + 1)/(2S + 1) и S/(2S + 1), где S – спин ядра, т.е.

b_coh = (S + 1)/(2S + 1)b₊ + S/(2S + 1)b_-, (3.16)

b_inc = (b₊ - b_-)·[S(S + 1)]^1/2/(2S + 1), (3.17)

где b₊ и b_- – длины рассеяния в состояниях S + 1/2 и S - 1/2.

Существуют таблицы (например, [7]), в которых собраны сведения о всех элементах таблицы Менделеева и о большинстве стабильных изотопов, включая когерентные и некогерентные длины и сечения рассеяния и сечения поглощения. В Интернете эти данные можно посмотреть по ссылке [8].

Выражение (3.9) для сечения рассеяния со структурным фактором в виде (3.11) используется при рассмотрении дифракции на монокристалле. Если же объектом исследования является поликристалл, то (3.9) должно быть усреднено по случайным ориентациям кристаллитов.

3.5. Специфика дифракции нейтронов на кристалле.

Сформулируем еще раз специфические особенности взаимодействия нейтронов низких энергий с веществом, особенно важные для структурной нейтронографии.

Длины рассеяния могут быть как положительными, так и отрицательными. Появляется возможность приготовить материал с нулевой когерентной длиной рассеяния, так называемую “нулевую матрицу”. Например, для Ti и Zr длины рассеяния b_Ti = -0.344, b_Zr = 0.716. Сплав, состоящий из 67.5%Ti и 32.5% Zr, имеет <b> ≈ 0 и, следовательно, не дает дифракционных пиков. Из такого сплава изготавливаются контейнеры для порошков.

Длины рассеяния нерегулярным образом изменяются от элемента к элементу. Как следствие по сравнению с рентгеновским структурным анализом существенно облегчается структурный анализ соединений, содержащих легкие и тяжелые атомы (гидридов, оксидов) и анализ соединений, содержащих элементы с близкими атомными номерами (интерметаллидов, сплавов).

Различные изотопы элемента имеют, как правило, разные длины рассеяния. Появляется возможность выделения отдельных фрагментов структуры путем внедрения специально подобранных изотопов, так называемое “изотопическое контрастирование”. Это оказалось особенно важным при исследовании органических и биологических структур, т.к. неразличимые для рентгеновских лучей водород и дейтерий хорошо различаются нейтронами (b_H = -0.374, b_D = 0.667, в единицах 10^{-12 см). Кроме того, изотопическое замещение в некоторых случаях помогает решить фазовую проблему (подробнее см. раздел 6.2).}

Длины ядерного рассеяния не зависят от переданного импульса. Это приводит к менее резкому спаду интенсивностей дифракционных пиков в области малых d_hkl, чем в случае рентгеновских лучей, что дает возможность более надежно определять тепловые факторы атомов. Измерение дифракционного спектра в области очень малых d_hkl (вплоть до 0.1 Å) позволяет получить информацию о локальных нарушениях структуры (подробнее см. раздел 7.5).

Длина магнитного рассеяния по величине близка к длинам ядерного рассеяния. Дифракция на кристаллах с дальним магнитным порядком дает возможность прямого анализа магнитной структуры – определения величин и направлений магнитных моментов атомов.

Для большинства элементов поглощение медленных нейтронов мало. Это определяет большую глубину проникновения нейтронов в образец (до нескольких сантиметров в сталях и алюминиевых сплавах), свойство исключительно важное в решении материаловедческих задач.

Взаимодействие нейтронов низких энергий с веществом относительно слабо в целом. Это свойство важно в двух отношениях. Во-первых, расчет сечений взаимодействия можно провести в первом борновском приближении и, соответственно, измеряемые эффекты легко интерпретируются. Во-вторых, вследствие слабого взаимодействия нейтроны не нарушают структуру и не изменяют химические свойства вещества, даже, несмотря на сравнительно длительные экспозиции.

Отметим для полноты еще и некоторые методические особенности нейтронного структурного эксперимента, которые подробно будут обсуждаться в следующей главе.

Возможны две альтернативные, взаимодополняющие и примерно эквивалентные постановки дифракционного эксперимента – с фиксированной длиной волны и разверткой по углу рассеяния, с “белым” исходным спектром и разверткой по времени пролета. Первый вариант используется, как правило, на стационарных (с постоянной во времени мощностью) реакторах, второй – на импульсных источниках нейтронов. Комбинация развертки по времени пролета и регистрации рассеянных нейтронов двухкоординатным позиционно-чувствительным детектором дает возможность организовать трехмерное сканирование обратного пространства кристалла в параллельном режиме.

Сечение нейтронного пучка может быть довольно большим, как правило, это несколько см². Это облегчает проведение экспериментов, требующих использования больших образцов как, например, в случае исследования крупноблочных текстур в металлах и минералах. Кроме того, большое сечение пучка позволяет заметно увеличить светосилу эксперимента.

Малое поглощение медленных нейтронов технологическими материалами резко облегчает проведение экспериментов в условиях сложного внешнего окружения образца – в криостатах и рефрижераторах, печах, камерах высокого давления и т.д.

Конечно же, у медленных нейтронов как инструмента для исследования структуры вещества есть немало недостатков, зачастую являющихся продолжением их достоинств. В первую очередь к ним следует малую по сравнению с рентгеновскими трубками и источниками синхротронного излучения светимость нейтронных источников. Поток нейтронов, как правило, недостаточно высок, продолжительность нейтронных экспериментов обычно излишне велика. Неприятной особенностью нейтронных экспериментов является активация образцов. Зачастую, даже после непродолжительной экспозиции на пучке образец приходится выдерживать в течение нескольких недель для исчезновения наведенной активности.