Уравнения массо-, тепло- и импульсопередачи

Локальная форма уравнений

Рассмотрим перенос субстанций из фазы 1 через межфазную поверхность в фазу 2 за счет молекулярного и турбулентного механизмов. Примем, что сопротивлением переносу субстанции со стороны межфазной поверхности можно пренебречь. Это равносильно предположению об установлении равновесия на границе раздела фаз, т.е.:

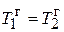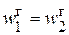, , . (2.77)

Рис 2.7. Схема межфазного переноса субстанций.

Предположим μ_i1>μ_i2, тогда;

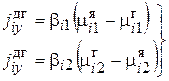. (2.78)

Разделим уравнения на β_i1 и β_i2 соответственно и их сложим:

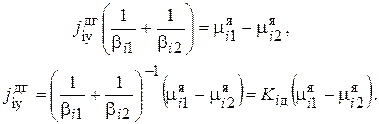(2.79)

Здесь 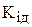- коэффициент массопередачи, 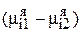- движущая сила массопередачи. Уравнение (2.79) носит название уравнения массопередачи.

Химические потенциалы неидеальных (реальных) систем определить достаточно сложно, поэтому при анализе и расчете процессов массопереноса обычно рассматривают изменение не химических потенциалов, а концентраций компонентов, определение которых значительно проще. Разность между рабочими и равновесными концентрациями компонента в одной из фаз являются движущей силой массообменного процесса.

Аналогичным образом могут быть получены уравнения тепло- и импульсопередачи:

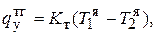
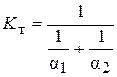, (2.80)

если Т₁>Т₂.

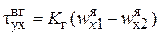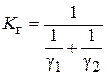, , (2.81)

если w_x1>w_x2

Здесь К_т и К_г – коэффициенты тепло- и импульсопередачи. Коэффициенты в соотношениях (2.79) – (2.81) могут быть представлены иначе:

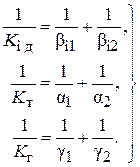, (2.82)

где 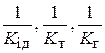- сопротивления массо-, тепло-, импульсопередачи (межфазные сопротивления), а 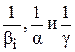- сопротивления массо-, тепло- и импульсоотдачи (фазовые сопротивления).

Соотношения (2.82) выражают аддитивность фазовых сопротивлений. Например, если процесс теплопередачи идет через стенку:

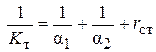, (2.83)

где r_ст – термическое сопротивление стенки.

Профили w_x, Т, μ_i в процессе переноса субстанции через границу раздела фаз, не обладающую сопротивлением, приведены на рис. 2.8.

Рис 2.8. Профили химических потенциалов, температуры и скорости в процессах переноса субстанций через границу раздела фаз

Здесь δ – толщина пограничных слоев.

Если сопротивление одной из фаз, например первой, гораздо больше второй, то последним можно пренебречь:

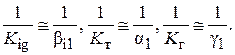(2.84)

Из (2.84) следует, что 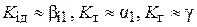при β_i1 << β_i2, α₁ << α₂, γ₁ << γ₂.

Интенсификация процессов переноса требует увеличения коэффициентов субстанциипередачи. Для этого необходимо увеличить наименьший коэффициент субстанцииотдачи.