Локальная форма уравнений
Уравнения массо-, тепло- и импульсоотдачи
Локальная форма уравнений
Рассмотрим элементарный участок межфазной поверхности dF, совпадающей с плоскостью xoy. Поток субстанций направлен вдоль оси z движение фазы по оси x (рис.2.5).
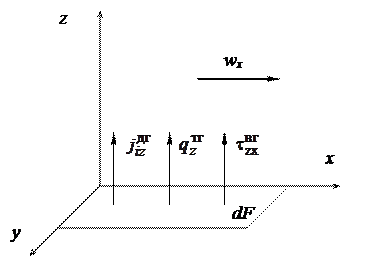 |
Рис 2.5. Перенос субстанций по оси z
Рассмотрим поток субстанции за счет молекулярного и турбулентного механизмов переноса:
- 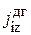 - диффузионный поток массы;
- диффузионный поток массы;
- 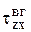 - вязкий поток импульса (тензор вязких напряжений);
- вязкий поток импульса (тензор вязких напряжений);
- 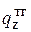 - поток тепла за счет теплопроводности.
- поток тепла за счет теплопроводности.
Проекция теплового потока за счет теплопроводности на ось z по закону Фурье имеет вид:
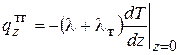 . (2.64)
. (2.64)
Использование этого закона затруднительно, так как неизвестен закон распределения температур в тепловом пограничном слое δт.
В тепловом пограничном слое δт температура среды меняется от 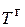 (температура поверхности раздела фаз) до
(температура поверхности раздела фаз) до 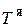 (температура на внешней границы пограничного слоя, т.е. температура ядра). В ядре фазы температура не меняется. По закону Ньютона тепловой поток
(температура на внешней границы пограничного слоя, т.е. температура ядра). В ядре фазы температура не меняется. По закону Ньютона тепловой поток 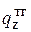 может быть записан:
может быть записан:
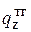 =α(
=α( 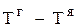 ), (2.65)
), (2.65)
где α – коэффициент теплоотдачи. Коэффициент теплоотдачи зависит от многих факторов: режима движения и физических свойств среды, геометрических параметров каналов и т.д.
Аналогичным образом могут быть получены уравнения массо- и импульсоотдачи:
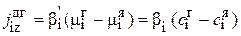 , (2.66)
, (2.66)
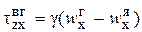 , (2.67)
, (2.67)
где βi, γ – коэффициенты массо- и импульсоотдачи.
Разница значений субстанций у границы раздела фаз и в ядре фазы носит название движущей силы субстанцииотдачи.
Коэффициенты массо-, тепло-, импульсоотдачи определяются:
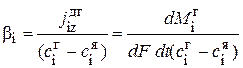 , м/с (2.68)
, м/с (2.68)
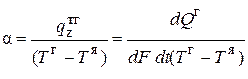 , Вт/(м2К) (2.69)
, Вт/(м2К) (2.69)
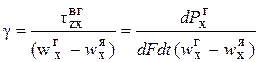 . кГ/ (м2с) (2.70)
. кГ/ (м2с) (2.70)
Следовательно, коэффициенты массо-, тепло-, импульсоотдачи являются кинетическими характеристиками этих процессов и отражают, соответственно, количество вещества (компонента), тепла и импульса, переносимое от границы раздела фаз к ядру фазы или в обратном направлении за единицу времени, через единицу межфазной поверхности и приходящиеся на единицу движущейся силы.
Коэффициенты массоотдачи рассмотрены для бинарных сред.
При ламинарном течении жидких сред вместо значения переменной в ядре потока в уравнениях (2.65) – (2.70) используют осредненное по поперечному сечению значение. Для ламинарного режима течения модель пограничного слоя «не работает».
Дата добавления: 2018-06-28; просмотров: 523;
