Методы определения дипольных моментов
Методы определения дипольных моментов основаны на нахождении ориентационного эффекта (за исключением метода молекулярного пучка) полярных молекул в приложенном электрическом поле. При этом следует учитывать, что если молекула является полярной и обладает дипольным моментом, то он называется постоянным или собственным дипольным моментом (μo). А при поляризации молекул в электрическом поле возникает индуцированный дипольный момент молекулы (μg). В статических полях или полях с относительно низкими частотами колебаний происходит поляризация вещества в целом, включающая также некоторое смещение ядер и ориентацию молекул вдоль поля, и возникает индуцированный ориентационный дипольный момент молекул (μr), который зависит от μo и из которого можно определить постоянный дипольный момент молекулы μo. Для точных измерений μo малых молекул применяются методы, основанные на микроволновой спектроскопии и молекулярных пучков. Особенно распространен метод Штарка, основанный на эффектах расщепления и сдвига спектральных линий в электрическом поле. Для линейных молекул известны точные выражения, связывающие дипольный момент со штарковским расщеплением линий вращательных спектров. Этот метод дает наиболее точные значения величины дипольного момента (до 10-4 D), причем экспериментально определяется не только величина, но и направление вектора дипольного момента. Важно, что точность определения дипольного момента почти не зависит от его абсолютной величины. Это позволило получить весьма точные значения очень малых дипольных моментов ряда молекул углеводородов, которые нельзя надежно определить другими методами. Так, дипольный момент пропана равен 0.085±0.001 D, пропилена – 0.364±0.002 D, пропина – 0.780±0.001 D, толуола – 0.375±0.01 D, азулена – 0.796±0.01 D. Область применения метода микроволновой спектроскопии ограничена небольшими молекулами, не содержащими атомов тяжелых элементов.
Из всех методов получили наиболее широкое распространение методы определения дипольных моментов, основанные на измерении диэлектрической проницаемости (ε) вещества. Этими методами измерены дипольные моменты молекул более 10000 веществ. Переход от измеряемого значения ε газа, чистой жидкости или разбавленного раствора, т.е. макроскопической характеристики диэлектрика, к величине дипольного момента основан на теории поляризации диэлектриков. Считается, что при наложении электрического поля на диэлектрик его полная поляризация Р складывается из наведенной или индуцированной поляризации Рм и поляризации Рор и связана с μ уравнением Ланжевена-Дебая (2).
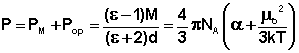 (2)
(2)
где М – молекулярная масса, d – плотность, α - поляризуемость молекулы, NA - число Авогадро, k – постоянная Больцмана, Т – абсолютная температура.
Измерения диэлектрической проницаемости проводят в постоянном поле или при низких частотах, обеспечивающих полную ориентацию молекул по полю. Кратко остановимся на типичной процедуре определения μо в разбавленных растворах. Она основана на предположении об аддитивности свойств составляющих раствор компонентов:
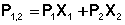 (3)
(3)
где Р1,2, Р1, Р2 – молекулярные поляризации раствора, растворителя и растворенного вещества соответственно;
Х1, Х2 – мольные доли растворителя и растворенного вещества.
С учетом уравнения (2) уравнение (3) для раствора будет выглядеть как (4):
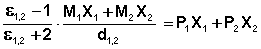 (4)
(4)
где М1 и М2 – молекулярные веса растворителя и растворенного вещества;
ε1,2 – диэлектрическая проницаемость раствора;
d1,2 – плотность раствора.
Из уравнения (4) можно вычислить Р2 – молекулярную поляризацию растворенного вещества. В этом методе допускается, что молекулы полярного вещества могут вести себя в растворах как в парообразном состоянии и свободно ориентироваться в приложенном поле только для бесконечно разбавленных растворов, поэтому значение Р2 следует экстраполировать на нулевую концентрацию (Х2 = 0) и найти значение молекулярной поляризации растворенного вещества при бесконечном разбавлении (Р2∞).
Эксперимент сводится к измерению диэлектрической проницаемости и плотности 5-7 разбавленных растворов исследуемого соединения при точно поддерживаемой температуре (обычно 25 °С) в интервале концентраций растворенного вещества от 0,001¸ 0,01 мольных долей. Выбор интервала концентраций зависит от растворимости и полярности вещества и может колебаться в сторону уменьшения мольных долей для более полярных соединений. Затем по формуле (4) находят значение молекулярной поляризации растворенного вещества для каждой концентрации и по полученным данным строят кривую зависимости Р2 от концентраций, по которой экстраполируют Р2 до нулевой концентрации и находят значение Р2∞. Эту величину можно также получить, используя различные приемы экстраполяции к нулевой концентрации для диэлектрической проницаемости и плотности.
Величину дипольного момента рассчитывают из уравнения Дебая (2)
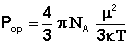
из которого, подставляя значения N, κ, π, можно вычислить величину постоянного дипольного момента по формуле (5):
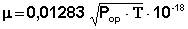 , эл.-ст. ед. (5)
, эл.-ст. ед. (5)
Найденное в эксперименте значение Р2∞ включает в себя электронную (Рэл) и атомную (Рат) молекулярные поляризации и поэтому Рор в уравнении (5) вычисляется как Рор = Р2∞ – Рат – Рэл.
Рэл считают равной рефракции вещества, которое вычисляется по той же схеме аддитивности на основании измерения коэффициентов преломления и плотности той же серии растворов, а Рат вследствие ее малости очень часто пренебрегают. Следует отметить, что Рэл можно рассчитать по рефракциям связей и групп, если не требуется высокая точность в значении дипольного момента.
Сходимость результатов, полученных различными методами при корректном использовании правильных расчетных формул бывает достаточно хорошей, как показано в табл. 1:
Таблица 1. Дипольные моменты молекул (в D)
| Соединение | По измерениям ε в бензоле, 25 ºС | В газе | По спектральным данным (эффект Штарка) |
| Вода | 1.83 | 1.84 | 1.85 |
| Аммиак | 1.41 | 1.48 | 1.48 |
| Дихлорметан | 1.55 | 1.57 | 1.62 |
| Ацетон | 2.83 | 2.85 | 2.90 |
| Ацетонитрил | 3.51 | 3.97 | 3.91 |
| Бромбензол | 1.57 | 1.64 | 1.66 |
| Пиридин | 2.20 | 2.23 | 2.15 |
Дата добавления: 2018-03-01; просмотров: 2655;
