Основы теории гидродинамического подобия
Известны два метода исследования физических явлений – аналитический и экспериментальный.
При аналитическом исследовании движения жидкости задача сводится к интегрированию системы дифференциальных уравнений при заданных условиях однозначности. Например, для вязкой несжимаемой жидкости система дифференциальных уравнений включает:
уравнения Навье – Стокса
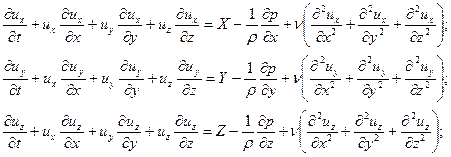
| (16.1) |
и уравнение неразрывности для несжимаемой жидкости
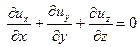
| (16.2) |
Уравнения Навье – Стокса Являются основными в гидромеханике вязкой жидкости и определяют течение реальной вязкой жидкости лишь тогда, когда подтверждается закон Ньютона о внутреннем трении в жидкости.
Если считать, что массовые силы (их проекции X, Y, Z на координатные оси) заданы, то система уравнений (16.1), (16.2)– это система уравнений с четырьмя неизвестными функциями 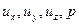 .
.
В принципе, эта система при заданных условиях однозначности дает возможность строгого решения задачи о движении вязкой несжимаемой жидкости. Однако аналитическое решение уравнений Навье – Стокса найдено лишь для ограниченного числа частных случаев.
Другим методом исследования физических процессов является непосредственный эксперимент. В этом случае измеряются те величины, которые представляют практический интерес, и находятся зависимости, допускающие непосредственное приложение. Недостатком такого метода исследования является то, что полученные результаты только к исследованному случаю и относятся. Задача обобщения данных опыта решается теорией подобия, которая является учением о методах обобщения данных опыта.
Основные понятия и определения теории подобия
Классом явлений называют совокупность явлений одной физической природы, которые описываются одной системой дифференциальных уравнений. Уравнения (16.1) и (16.2) описываются все возможные виды течения вязкой несжимаемой жидкости в каналах любой формы.
Под единичным явлением понимается система дифференциальных уравнений с наложенными на нее условиями однозначности (начальными и граничными условиями) - течение жидкости в канале заданной геометрической формы.
Под группой явлений понимается система дифференциальных уравнений с наложенными на нее подобными условиями однозначности. Группу явлений, например, образуют задачи течения жидкости в геометрически подобных каналах.
Основная идея теории подобия состоит в выделении внутри класса явлений более узких групп.
Подобными явлениями называют такие, у которых отношение характеризующих их переменных есть постоянное число.
Различают следующие виды подобия:
1. Для того, чтобы модель была механически подобна (объекту, для которого создается модель), прежде всего, должно соблюдаться геометрическое подобие. Для этого отношение длин сходственных отрезков образца и модели должны быть одинаковыми, т.е.
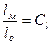 , ,
| (16.3) |
где 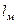 - некоторый линейный размер потока модели;
- некоторый линейный размер потока модели;
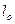 - соответствующий линейный размер потока в образце;
- соответствующий линейный размер потока в образце;
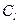 - константа геометрического подобия.
- константа геометрического подобия.
Из последней формулы следуют соотношения
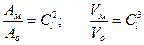 , ,
| (16.4) |
где 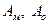 - соответствующие площади модели и образца;
- соответствующие площади модели и образца;
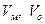 - соответствующие объемы модели и образца.
- соответствующие объемы модели и образца.
2. При построении модели, кроме геометрического подобия, необходимо соблюдать еще динамическое подобие, которое означает, что все силы, вызывающие движение в модели, должны быть изменены с аналогичными силами в образце в одно и тоже число раз.
Сила 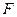 определяется по закону Ньютона
определяется по закону Ньютона
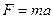 . .
| (16.5) |
Это определяет ее размерность через плотность жидкости, геометрический размер и скорость (кинематический параметр)
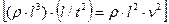 . .
| (16.6) |
Отсюда следует, что для динамического подобия необходимо соблюдение следующего соотношения
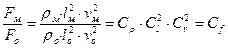 , ,
| (16.7) |
здесь 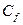 - константа динамического подобия, определяемая через константы подобия плотности жидкости, константу геометрического подобия и константу подобия скорости. Условие (…) является математическим выражением общего закона динамического подобия, сформулированного Ньютоном.
- константа динамического подобия, определяемая через константы подобия плотности жидкости, константу геометрического подобия и константу подобия скорости. Условие (…) является математическим выражением общего закона динамического подобия, сформулированного Ньютоном.
В теории подобия доказывается, что при выполнении геометрического и динамического подобий будет соблюдаться и кинематическое подобие. Следовательно, скорости, ускорения, перемещения частиц в модели будут изменяться в одних и тех же отношениях по сравнению с образцами. В двух подобных явлениях должны существовать соотношения типа
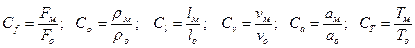 и т. д., и т. д.,
| (16.8) |
где константы подобия сохраняют постоянные значения в сходственных точках подобных систем.
Подобных явлений бывает не два, а бесконечное множество. Эти явления составляют группу подобных явлений.
Дата добавления: 2017-12-07; просмотров: 1529;
