Теоремы подобия. Критерии подобия.

Очевидно, что подобные явления должны принадлежать лишь к одному классу, т.е. описываться одной и той же системой дифференциальных уравнений. Если применить дифференциальные уравнения к образцу и модели, то можно получить некоторые условия, которым должны удовлетворять константы подобия. Эти условия обеспечивают удовлетворение переменных образцового явления и переменных модельного явления одному и тому же уравнению.

Переменные образцового явления обозначим 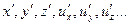, а переменные модельного явления обозначим 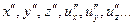. Запишем, для примера, одно из уравнений Навье – Стокса для образцового явления

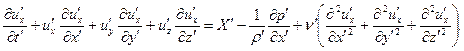
(16.9)

Для явления, протекающего в модели, но подобного образцовому, должны выполняться зависимости, содержащие константы подобия

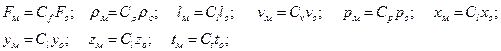
(16.10)

Уравнение (…) для модели имеет вид аналогичный, но относительно других переменных

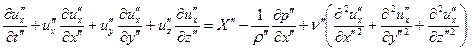
(16.11)

Подставляя (16.10) в уравнение (16.11) и учитывая, что константы подобия 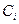постоянны и при дифференцировании выносятся за знак дифференциала, получим

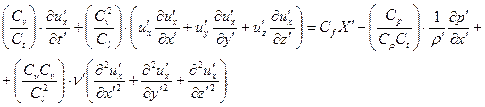
(16.12)

Результат (16.12) показывает, что для совместности уравнений (16.9) и (16.11), т.е. для того чтобы переменные первого и второго явлений удовлетворяли бы одному и тому же дифференциальному уравнения, должны удовлетворяться следующие равенства

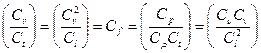
(16.12)

Разделив равенство (16.12) на 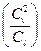, получим

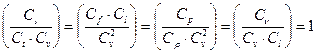
(16.12)

Поменяв числитель и знаменатель в первом и последнем отношениях местами, получим

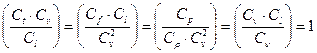
(16.12)

Используя определения констант подобия (16.10), найдем комплексы величин, которые, в соответствующих точках образца и модели, должны быть одинаковыми

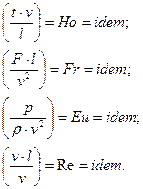
(16.12)

Величины 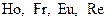называют критериями подобия или числами подобия (не путать с константами подобия). 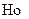- критерий гомохронности; 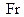- критерий Фруда, 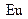- критерий Эйлера; 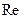- критерий Рейнольдса.

Критерии или числа подобия позволяют сформулировать следующие теоремы подобия:

Первая теорема подобия: у подобных явлений для любой пары сходственных точек критерии подобия численно одинаковы.

Так как отдельные явления различаются между собой лишь условиями однозначности (начальными и граничными условиями), то если условия однозначности сделать подобными, подобными окажутся и сами явления, если они описываются одними и теми же дифференциальными уравнениями.

Но для подобия условий однозначности достаточно соблюсти равенство критериев подобия, составленных лишь из величин, входящих в условия однозначности. Поэтому можно сформулировать следующее утверждение, известное, как третья теорема подобия: подобны те явления, условия однозначности которых подобны, а критерии подобия составленные из величин, входящих в условия однозначности, равны.

Значение этой теорем состоит в том, что она обосновывает моделирование явлений. Чтобы модель была подобна образцу, достаточно осуществить пропорциональность всех величин на границе явления и в начальный момент времени, выбрав эти величины так, чтобы критерии, составленные их них, были численно равны для соответствующих точек модели и образца. Например, при течении жидкости в гладкой круглой трубе в условия однозначности входят 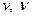. Поэтому для подобных явлений должно выполняться условие 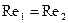или .

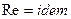Все критерии, полученные из данной системы уравнений, можно разбить на две категории. К первой категории относятся критерии, составленные из величин, входящих в условия однозначности. Эти критерии называют определяющим, так как они определяют достаточные условия подобия. Ко второй – все остальные критерии, получающиеся из системы уравнений. Их называют неопределяющими.

Если значения определяющих критериев у двух явлений в соответственных точках равны, то явления подобны. Если они подобны , то по первой теореме подобия они имеют в соответственных точках одинаковые значения всех критериев, независимо от того, к какой из двух категорий они относятся. Отсюда следует, что равенство определяющих критериев имеет следствием равенство всех остальных критериев. Это, в свою очередь, означает, что между определяющими и неопределяющими критериями существует функциональная зависимость.

В самом деле, если от одних значений определяющих критериев перейти к другим, то это будет означать переход от одной группы подобных явлений к другой. При этом неопределяющие критерии получат какие-то новые единственные значения. Таким образом, каждый неопределяющий критерий есть однозначная функция определяющих критериев. Например, если определяющим критерием является критерий Рейнольдса, то критерий Эйлера будет его функцией .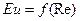

Вид этой функции может быть найден из опыта. Если эта зависимость представлена в виде графика, то каждая точка на этом графике будет отвечать целой группе подобных явлений, для которых 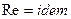, а вся кривая будет соответствовать серии групп.

Между тем каждая точка может быть получена в результате единичного опыта, а вся кривая – в результате серии экспериментов на одной установке.

Таким образом, результаты небольшого числа экспериментов можно обобщить на целую группу явлений и получить решение или интеграл дифференциального уравнения в виде критериального уравнения, что соответствует второй теореме подобия: решение системы дифференциальных уравнений может быть представлено в виде функции между критериями подобия этой системы.

Это позволяет не интегрировать систему дифференциальных уравнений, а получить ее интеграл в виде критериального уравнения из опыта.