Скорость распространения гидравлической ударной волны

Рассмотрим продвижение фронта ударной волны на участке трубопровода длиной 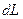(рис. 15.10).

Предположим, что в момент времени 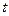в сечении 1-1 давление увеличится на величину 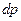. Это увеличение давления приводит к увеличению плотности жидкости на величину 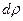, вызывает дополнительную деформацию трубы – площадь поперечного сечения которой возрастет на величину 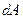. Приращение объема трубы на участке 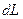составит 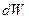единиц объема. Масса жидкости на участке трубопровода длиной 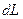возрастет, как за счет увеличения плотности, так и за счет увеличения объема. В начальный момент времени 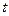масса жидкости в трубопроводе была равна 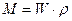. Изменение массы жидкости при увеличении давления на величину 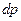составит

.

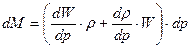(15.1)

Жидкость из области повышенного давления 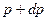будет перемещаться в область пониженного давления, деформируя стенку трубы. Если принять, что скорость движения жидкости величина постоянная равная 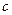, время движения ударной волны на участке 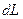составит

.

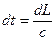(15.2)

Перемещение массы жидкости 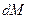происходит под действием результирующей сил давления (трением пренебрегаем), действующих на торцевых сечениях объема длиной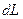

.

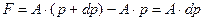(15.3)

Перемещаемая масса жидкости 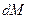за время 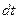изменяет скорость от значения равного нулю до значения 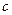. Тогда, согласно теореме об изменении количества движения, можно записать

.

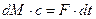(15.4)

С учетом (15.2) и (15.3) последняя формула принимает вид

.

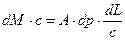(15.4)

Из формулы (15.4) с учетом (15.1) находим

.

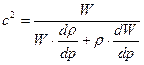(15.6)

После деления числителя и знаменателя на 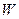, умножения и деления первого слагаемого знаменателя на 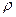, получим следующую формулу для определения скорости распространения ударной волны

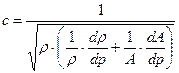
(15.7)

Первое слагаемое под корнем определяется упругими свойствами жидкости, а второе – упругими характеристиками трубы. Рассмотрим эти слагаемые подробнее.

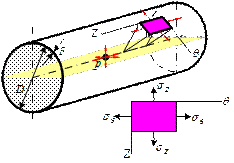
Изменение площади поперечного сечения трубы связано с ее деформацией в радиальном направлении. Из курса сопротивления материалов известно, что напряженное состояние тонкостенной цилиндрической оболочки определяется напряжениями на площадках перпендикулярных оси трубы и площадках параллельных образующей (рис. 15. 11).

Так как труба не нагружена растягивающими усилиями в осевом направлении, легко найти, что 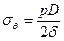. Тогда относительная деформация трубы в окружном направлении при увеличении давления на 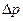равна

,

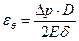(15.8)

что соответствует абсолютному увеличению диаметра трубы

.

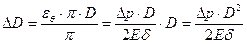(15.9)

Этому изменению диаметра трубы соответствует следующее изменение площади поперечного сечения

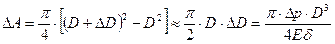
(15.10)

Теперь находим

.

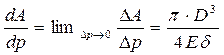(15.11)

Второе слагаемое в знаменателе формулы (…) принимает вид

.

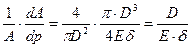(15.12)

Первое слагаемое под корнем формулы ( ) определяется модулем упругости жидкости (см. (6) и (7) в лекции 1)

,

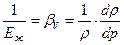(15.13)

что позволяет переписать формулу (15.7) в следующем виде

,

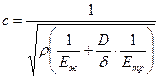(15.14)

где

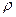· - плотность жидкости;

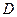· - диаметр трубопровода;

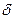· - толщина стенки трубопровода;

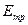· - модуль упругости материала трубы;

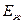· - объемный модуль упругости жидкости.

Ударное давление

Величина повышения давления 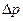, от которой зависит прочность трубопровода, существенна для понимания последствий гидравлического удара для трубопровода.

Для определения величины 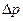воспользуемся теоремой об изменении количества движения, применив ее к движению массы жидкости 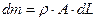, располагающейся на фронте ударной волны (рис.15. ..).

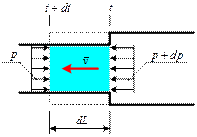
Рис.15.

Масса жидкости 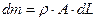за время 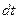увеличивает скорость движения от нуля до значения 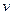. Импульс сил, действующих на выделенный объем, за время 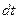равен

.

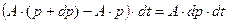Согласно теореме об изменении количества движения в интегральной форме

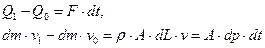
Отсюда приращение давления на фронте ударной волны равно

,

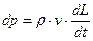где 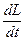- скорость распространения ударной волны.

Если в формулу (…) подставить выражение, определяющее скорость распространения ударной волны (…), то получим величину приращения давления при гидроударе

.

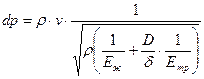Для примера определим скорость распространения ударной волны и повышение давления в стальной трубе диаметром 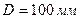при толщине стенки 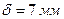, заполненной водой при температуре 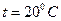, когда 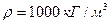, модуль объемного сжатия жидкости 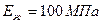, модуль продольной упругости материала трубы (сталь) 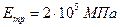и скорости движения жидкости в трубопроводе :

,

.

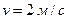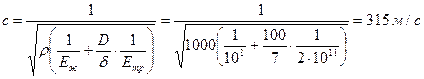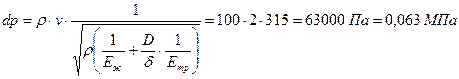Что составит от рабочего давления в трубопроводе существенную величину, даже при избыточном давлении 0,3 МПа

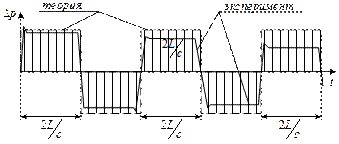
Рассмотренный процесс движения ударной волны не протекает бесконечно долго из-за рассеивания кинетической энергии потока. В опытах Н.Е. Жуковского было зарегистрировано до 12 циклов с последовательным уменьшением величины 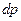, что иллюстрирует рис. 15. … .

Рис.

На графике прерывистой линией показана теоретическая зависимость приращения давления во времени, а сплошной линией – примерный