Тождества теории множеств
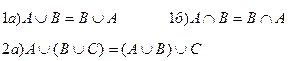
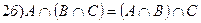
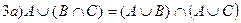
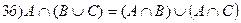
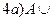 Æ=A
Æ=A
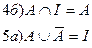
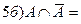 Æ
Æ
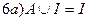
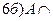 Æ=Æ
Æ=Æ
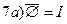
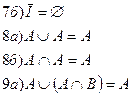
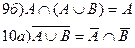
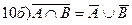
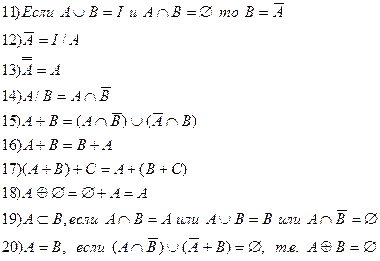
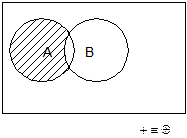
Важнейшие зависимости ФАЛ.
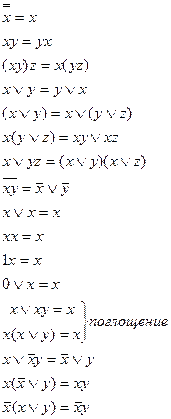
Вопросы
1. Основные понятия и терминология теории множеств:
множество, элемент, конечные и бесконечные способы задания множеств, ординарность, экстраординарность, пустое множество, собственное, несобственное, симметричное, рефлексивность, транзитивность.
2. Взаимно одиозное соответствие между множествами.
3. Счетные и несчетные множества.
4. Верхняя и нижняя границы множеств.
5. Операции над множествами.
6. Универсальное множество, дополнение множест
7. Разбиения множества.
8. Тождества алгебры множеств.
9. Коммутативные и дистрибутивные законы.
10. Теоремы де Моргана в алгебре множеств.
11. Дизъюнктивная сумма (коммутативный и распространительный законы).
12. Принципы двойственности.
13. Метод доказательств тождеств.
14. Отношение в множествах:
рефлексивность, нерефлексивность, антирефлексивность, сим метричность, асимметричность, транзитивность, связанность (доказать приведением высказываний).
15. (M/N)Ç(N/M)=?
(АÇВÇС)È( 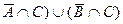 =?
=?
16. Решить уравнение 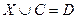
17. Принцип решения уравнений.
18. Круги Эйлера для доказательства тождеств.
19. Круги Эйлера при решении уравнений.
20. Диаграммы Венна для доказательства тождеств.
21. Диаграмма Венна для решения тождеств.
22. Сравнительный анализ методологии применения кругов Эйлера и диаграмм Венна.
23. Произведение множеств.
24. Области определения и значений.
25. Сечения, матрица отношений.
26. Граф отношения, симметричное отношение.
27. Композиция отношений.
28. Общие свойства отношений.
29. См. примеры 65.
30. Произведение множеств. Проекция множеств.
31. Соответствие в множествах.
32. Обратное соответствие. Способы задания соответствий.
33. Композиция соответствий.
34. Графическое задание объединения и пересечения соответствий.
35. Отображения, свойства их, композиция соответствий.
36. Отображение как функция.
37. Способы задания функции.
38. Функция времени, понятие оператора.
39. Понятие изоморфизма.
Комбинаторика
1. Выборка элементов. Правило суммы и произведение.
2. Перестановки.
3. Сочетание.
4. Рекуррентные соотношения.
5. Бином Ньютона.
6. Принцип включения и исключения.
Дата добавления: 2017-11-04; просмотров: 1708;
