Типы конечных графов.

Число ребер, связанных с вершиной n_i (петля учитывается два­жды), называется степенью вершины и обозначается deg(n_i).

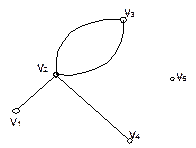
deg(n₂)=4

deg(n₅)=0

Степень изилирования вершины равна 0. Легко показать, что в любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно.

В орграфе различают положительные d ⁺(n_i) и отрицательные d ^-(n_i) степени вершин, которые равны соответственно числу исходящих из n_i и заходящих в n_i дуг.

Очевидно, что суммы положительных…………………………….

Примеры и задачи.

1. Даны два множества Х={x₁,x₂,x₃,x₄,x₅,x₆} Y={y₁,y₂,y₃,y₄}

и определено бинарное отношение А={(x₁,y₂),(x₂,y₁),(x₂,y₂),(x₄,y₂), (x₄,y₃),(x₅,y₁),(x₅,y₃)}.

Для данного отношения А:

а) записать область определения и область значений;

б) определить сечения по каждому элементу из Х;

в) определить сечения по подмножествам Х'={x₁,x₄} и Х''={x₂,x₃,x₅} множества Х;

г) записать матрицу и нарисовать граф;

д) определить симметричное отношение А^-1.

2. Пусть Х — множество студентов; Y — множество дисциплин и соотношение хАу, где хÎХ и уÎY, означает ''студент х изучает дис­циплину у''. Дать словесное описание областей определения и значе­ний, сечений и обратного отношения, полученных в задаче №1.

3. По результатам задачи определите множества А(х₂) Ç А(х₄), А(х₂)\ А(х₄) и А(х₂)+А(х₄). Дайте им словесное описание согласно условия задачи №2.

Задача. Представьте бинарные отношения, заданные графом как множество упорядоченных пар и запишите его матрицу.

Задача. Записать композицию С=ВА отношений А={(1,2),(1,3), (2,1),(2,4),(3,3)} и В={(1,1),(1,3), (2,2),(3,1),(4,2),(4,3)}. Проверить результат с помощью операций над матрицами и графами заданных отношений.