Экстремальное дерево.

В ряде практических задач требуется связать р пунктов наибо­лее экономичным способом с линиями связи р пунктов, автомобиль­ными дорогами таким образом, чтобы суммарная длина была наи­меньшей.

На языке теории графов эта задача формулируется в общем виде следующим образом.

Каждому ребру (n_i,n_j) полного графа с р вершинами приписыва­ется вес m_ij, выражающий численно расстояние, стоимость и другую величину, характеризующую любую пару вершин.

Требуется построить экстремальное дерево, связывающее все вершины так, чтобы был минимальным суммарный вес m_i ветвей дерева

.

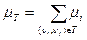Перебор вариантов при р³9 больше 10⁶. Существует алгоритм Прима, который основан на последовательном введении выбора ре­бер с наименьшим весом. Затем на каждом следующем шаге выби­рается min по весу ребро и, если оно не образует цикла с ранее вы­бранными ветвями, вводится в дерево. Построение заканчивается после отбора дерева (р-1) ребер. Если имеются ребра с одинаковым весом, то решение может быть единственным в том случае, когда не все такие ребра входят в дерево, а отдается определенный приоритет отдельным.

Построение экстремального дерева с максимальным суммар­ным весом аналогично, необходимо лишь последовательно выбирать для него ребра наибольшего веса.

Деревья графа.

Будем называть деревом связного графа любое покрывающее дерево, связывающее все его вершины и имеющее в качестве ветвей ребра этого графа.

Два дерева считаются различными, если они отличаются хотя бы одним ребром.

Существует простой способ определения количества различных деревьев графа без петель (мультиграфа) с р вершинами. Для этого необходимо записать квадратичную матрицу р-го порядка, по глав­ной диагонали которой расположена степень вершин, а ij-и ji-элементы равны взятому со знаком ''-'' числу ребер, связывающих вершины i и j.

Вычисляя любой из главных минора этой матрицы, получим исходное число деревьев.

Например, для графа имеем дерево (одно из 7в).

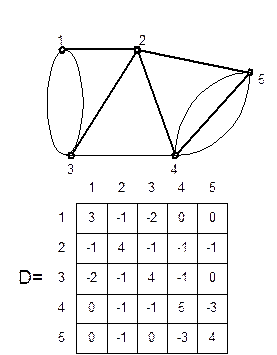
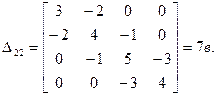
D₂₂ — один из главных миноров этой матрицы.

Это теорема Трента.