Проблема разрешимости тождественной истинности

Ввиду особой роли ТИФ, возникает вопрос о существовании общего метода (разрешающего метода), позволяющего относительно любой конкретной формулы логики высказываний ответить, является ли она тождественно истинной или нет.

Укажем несколько методов разрешения этого вопроса.

1. Составление таблицы истинности, соответствующей данной формуле. Если последний столбец таблицы (столбец значений данной формулы) состоит из одни И, данная формула – ТИФ, если же в столбце содержится хотя бы одна Л, она не является ТИФ. Разумеется, составление таблицы истинности ‑ не всегда удобный метод (при числе n переменных таблица содержит 2ⁿ строк). Но она всегда состоит из конечного числа шагов и всегда дает ответ на поставленный вопрос.

2. Преобразование формулы (приведение ее к КНФ). Все операции, знаки, которые содержатся в формуле, выражаются через конъюнкцию, дизъюнкцию и отрицание. Знаки отрицания сводятся к отдельным переменным (использование законов де Моргана). Для этого используются законы двойного отрицания, коммутативности, ассоциативности конъюнкции и дизъюнкции, дистрибутивности дизъюнкции относительно конъюнкции.

В результате этих преобразований формула приводится к КНФ. Если в каждой дизъюнкции содержится какая-либо переменная вместе с ее отрицанием, то данная формула – ТИФ. Если существует хотя бы одна дизъюнкция, не содержащая ни одной переменной вместе с ее отрицанием, данная формула не является ТИФ.

Пример. Применим этот метод к формуле (pÞq)(qÞr) Þ (pÞr)

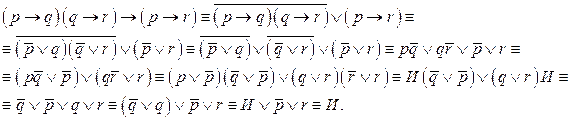
3. Метод косвенного доказательства (способ от противного). Допустим, что данная формула не является ТИФ. Тогда существует хотя бы один набор значений переменных, входящих в эту формулу, при котором она принимает значение Л. Если такой набор переменных удается найти, то данная формула не является ТИФ. Если же допущение о существовании такого набора значений переменных ведет к противоречию, то данная формула – ТИФ.

Пример. Применим этот метод к формуле (pÞq)(qÞr) Þ (pÞr).

Допустим, что эта формула не является ТИФ. Тогда существует хотя бы один набор значений переменных (p, q, r), при котором она ложна, то есть основание истинно

(pÞq)(qÞr)ºИ; (1)

а следствие ложно (pÞr)ºЛ. (2)

Из (2) следует р=И, (3)

а r=Л (4)

Из (1) следует, что (pÞq)ºИ; (5)

(qÞr)ºИ; (6)

Из (6) и (4) следует q=Л, (7)

а из (7) и (5) р=Л. (8)

Получили противоречие (3) и (8). Следовательно, наше допущение неверно и формула (1) ТИФ.

На основе этих примеров можно сделать ряд выводов о тождественной истинности формул.

Теорема 1. Чтобы элементарная логическая сумма была тождественно-истинной, необходимо и достаточно, чтобы в ней содержалась хотя бы одна пара слагаемых, из которых одно есть некоторая переменна, а другое – ее отрицание.

В самом деле, если такая пара слагаемых найдется, то сумма имеет вид 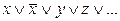Поскольку 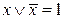, поэтому и истинна вся рассматриваемая сумма, каковы бы ни были остальные слагаемые y, z,…

Это условие достаточное. Теперь об условии необходимом. Допустим, что такой пары слагаемых, из которых одно является отрицанием другого, в сумме нет. В таком случае можно каждой переменной, не стоящей под знаком отрицания, дать значение Л, а каждой переменной, стоящей под знаком отрицание дать значение И. Это можно сделать, поскольку ни одна переменная не входит в сумму одновременно с отрицанием и без отрицания. После указанной подстановки каждое слагаемое примет значение Л, и, следовательно, формула не является ТИФ, что и требовалось доказать.

Аналогично доказывается

Теорема 2. Чтобы элементарное произведение было тождественно ложным, необходимо и достаточно, чтобы в нем содержалась хотя бы одна пара множителей, из которых один является отрицанием другого.