Элементы теории графов

Теория графов представляет в распоряжение инженера исклю­чительно удобный аппарат для моделирования структурных свойств систем и отношений между объектами самой разнообразной при­роды. На основе аналогии между физическими величинами развива­ется методика построения математических моделей систем в раз­личной форме.

Основные понятия и определения

Граф — это система некоторых объектов вместе с парами этих объектов, изображаются отношения связи между ними.

Графом G называется система (V,U,j), где V={n} — множество вершин; U={u} — множество ребер; j — функция инциденции, ста­вящая в соответствие каждому ребру uÎU упорядоченную (или не­упорядоченную) пару вершин (n₁,n₂), называемых концами ребра u.

Множество vUu образует множество элементов графа. По количеству элементов графы делятся на конечные и бесконечные.

Если j(u)= (n₁,n₂) — упорядоченная пара, (т.е. (n₁ ¹n₂)Ù(n₁,n₂)¹ (n₂,n₁)), то ребро n называется ориентированным ребром или дугой, исходящей из вершины n₁ (начало), и входящей в вершину n₂ (конец дуги).

Если j(u)=(n₁,n₂) — неориентированная пара, то соответствую­щее ей ребро — неориентированное.

Граф с неориентированными ребрами называют неориентиро­ванным, а с ориентированными ребрами — неориентированным графом (орграфом).

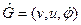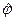Всякому графу G(v,u,j) можно сопоставить соотнесенный не­ориентированный граф , где — сопоставляет ребрам те же пары вершин, что и j, но неупорядоченные.

Граф, имеющий как ориентированные, так и неориентирован­ные ребра, называется смешанным.

Граф G=(v,u,j), ребрами которого являются всевозможными пары j(u)=(n_i,n_j) для двух возможных вершин n_i,n_jÎV, называется полным неориентированным графом. Такие графы для трех, четырех и пяти вершин приведены:

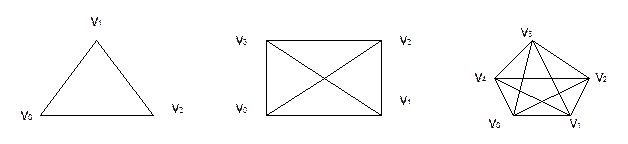
Граф G=(v,u,j), в котором пара вершин соединяется несколькими (кратными) ребрамиб называется мультиграфом, а содержащий изолированные вершины — нуль-графом.

Дополнением графа G=(v,u,j) является граф G_к=(v,u,j), ребра которого совместно с графом G образуют полный граф.

Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. В общем случае граф может содержать изолированные вершины, которые являются концами ребер и не связаны между собой, ни с другими вершинами.

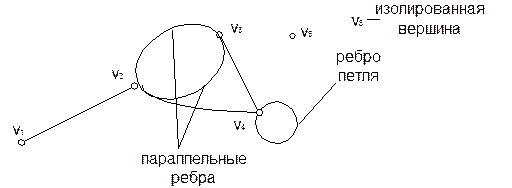
Число ребер, связанных с вершиной n_i (петля учитывается два­жды), называют степенью вершины.