Деревья на множестве вершин

Пусть множество v содержит р вершин, которые пронумерованы v₁,… v_р. Связав эти вершины (р-1) ребрами так, чтобы отсутствовали циклы, получим некоторое дерево, покрывающее данное множество р вершин. При р=2 такое дерево единственное и состоит из одной ветви. С увеличением р число различных деревьев t_p быстро возрастает

t_p=р^р-2

многие из них являются изоморфными, т.е. отличаются только нумерацией вершин. Так при р=0 имеем 10⁸ различных деревьев, из которых 106 неизоморфны.

На рис. показаны 16 различных деревьев, которые можно построить на множестве четырех вершин.

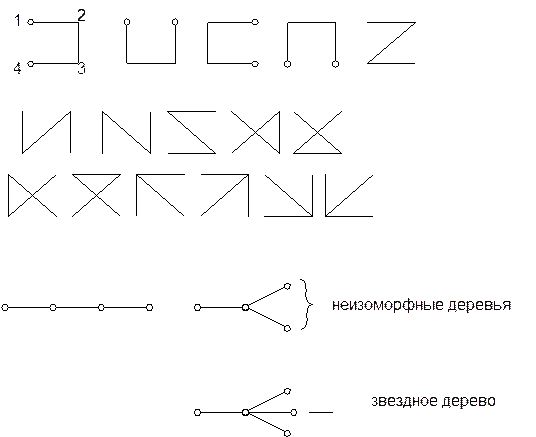
Символ дерева

Любому дереву Т можно поставить во взаимно-однозначное соответствие некоторый символ — упорядоченную последовательность (р-2) номеров вершин a(Т)=(a₁,a₂,… a_р-2), среди которых могут быть повторяющиеся, причем a₁,a₂,… a_р-2În.

Эта последовательность для данного дерева образуется следующим образом.

Вводится последовательность N_p=(1,2,…р), далее выбирается концевая вершина с наименьшим номером и записывается номер a,связанной с ней вершиной, а сама концевая вершина удаляется из последовательности N_p=(1,2,…р). Затем этот процесс повторяется до тех пор, пока не получим последовательность a(Т)=(a₁,a₂,… a_р-2). Каждый такой шаг соответствует удалению из дерева концевой вершины с наименьшим номером и связанного с ней концевого ребра, причем (р-2) шагов от дерева остается единственное ребро, положение которого определяется парой номеров вершин, остав­шихся в последовательности N_p. Построение дерева по его символу выполняется последовательным восстановлением концевых вершин и ребер.

На первом шаге из последовательности N_p=(1,2,…р) выбирается наименьший номер a_min, который отсутствует в a(Т)=(a₁,a₂,… a_р-2) и строится ребро (a_min,a₁). Далее удаляется номер a_min из N_p и номер a₁ из a(Т) и процесс продолжается до исчерпывания символа a(Т). оставшаяся в последовательности N_p пара вершин определяет последнее ребро дерева.

Например, исходя из символа a(Т₂)=(1,3,1,1,3) дерева Т₂

.

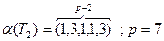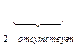
последовательность N₇=(1,2,3,4,5,6,7) на первом шаге имеем ребро (2,1). Удаляя ''2'' из N₇ и ''1'' из a(Т₂), получаем последовательность

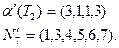
На втором шаге получаем ребро (4,3) и далее аналогично ребра (5,1),(6,1),(1,3),(3,7). Совокупность всех полученных ребер и обра­зует соответствующее дерево.

Произвольное дерево на множестве р вершин можно рассмат­ривать как одно из покрывающих деревьев графа.

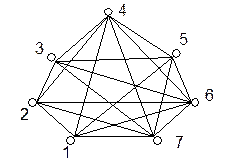
Рис. Дерево полного графа.